Базис векторного пространства и преобразование координат

Определение. Векторы 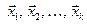называются линейно независимыми, если равенство 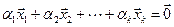возможно тогда и только тогда, когда все числа 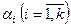равны нулю. В противном случае векторы 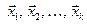называются линейно зависимыми.

Определение. Система линейно независимых векторов 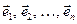в пространстве 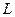образует его базис, если 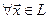существует разложение

,

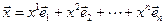где 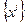- элементы поля 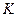, над которым задано векторное пространство 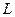. Числа 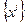называются координатами вектора 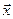относительно базиса .

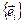Теорема. Координаты вектора относительно заданного базиса определяются однозначно.

Отметим, что число базисных векторов определяет размерность векторного пространства.

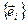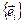Рассмотрим два базиса и (штрихованный и не штрихованный) пространства 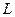. Разложим один и тот же вектор относительно этих базисов

,

.

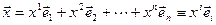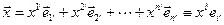(Здесь использовано обозначение Эйнштейна: если в формуле верхний и нижний индекс совпадает, то по этому индексу подразумевается суммирование). Видим, что при переходе к другому базису меняются координаты вектора (но не сам вектор!). Для нахождения формул преобразования координат, разложим векторы штрихованного базиса по не штрихованному базису

,

,

………………………..

.

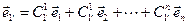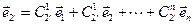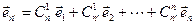Определенная таким образом матрица

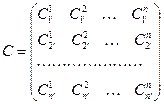
называется матрицей преобразования базиса к базису 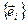( или матрицей перехода от базиса 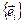к базису 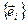. Подставим формулу 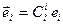в разложение вектора 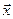относительно штрихованного базиса

.

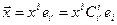Поскольку координаты вектора относительно базиса определяются однозначно, получаем 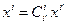. Обратим это равенство. С этой целью умножим левую и правую части этого равенства на элементы новой матрицы 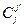: 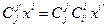. «Свернем» это равенство по индексам 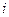и 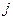, т.е. приравняем их и возьмем сумму по единому индексу, 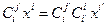. Определим новую матрицу 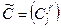равенством 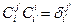, где 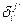- символ Кронекера. Тогда 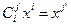или 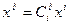. Следовательно, координаты вектора преобразуются с помощью матрицы 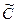, являющейся обратной к матрице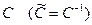

Замечание. Образуем матрицы , ,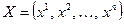

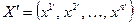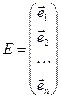и .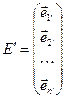

Формулы разложения вектора по базисам на матричном языке имеют вид 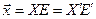, а формулы преобразований базисов и координат записываются следующим образом .

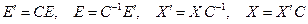3.Гомоморфные и изоморфные отображения векторных пространств, линейные операторы, матрица оператора, собственные значения и собственные вектора оператора.

Определение. Пусть 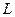и 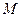- два векторных пространства. Отображение 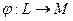называется гомеоморфным отображением или гомеоморфизмом, если оно сохраняет линейные операции, т.е. если выполняется равенство

.

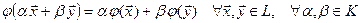Определение. Взаимно однозначное гомоморфное отображение 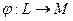называется изоморфным отображением или изоморфизмом. Если такое отображение 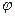существует, то пространства 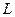и 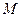называются изоморфными.

Определение. Гомоморфное отображение 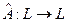называется линейным оператором на пространстве .

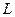Множество линейных операторов на пространстве 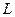можно превратить в векторное пространство, задав сумму операторов правилом 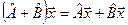и произведение оператора на число 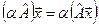. Каждому оператору можно поставить в соответствие матрицу, если выбрать некоторый базис 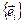пространства 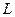. Подействуем оператором 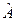на каждый базисный вектор и разложим получающиеся векторы по базису

,

,

…………………………

.

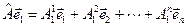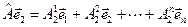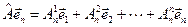Матрица

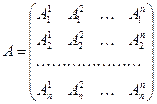
называется матрицей оператора 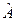относительно базиса 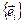. При фиксированном базисе пространства 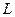любая 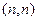-матрица определяет оператор на этом пространстве. Действительно,

,

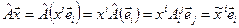где 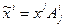. Взаимно однозначное соответствие между операторами и их матрицами определяет изоморфизм между векторным пространством операторов и векторным пространством 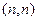-матриц. Так как изоморфные пространства имеют одинаковую размерность, размерность векторного пространства операторов равна 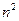. При выборе другого базиса 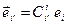пространства 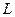меняется матрица оператора (сам оператор не меняется, так как является вектором). Правило преобразования матрицы оператора имеет вид .

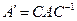Определение. Вектор 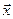называется собственным вектором оператора 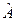, если 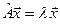, где 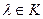называется собственным значением оператора .

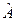4. Группы преобразований векторных пространств.

5.Сопряженные пространства, пространства билинейных функционалов.

Определение. Сопряженным (или дуальным, или двойственным)векторным пространством 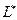к пространству 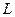называется векторное пространство линейных отображений (форм, функционалов) 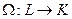таких, что 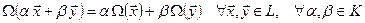. Сумма векторов в пространстве 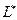вводится правилом 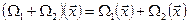, а умножение на число определяется следующим образом .

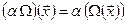Определение. Отображение 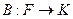называется билинейным функционалом на 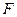, если при фиксированном значении одного аргумента оно является линейным функционалом относительно другого, т.е.

,

.

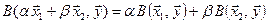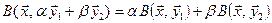
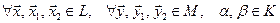6. Скалярное произведение, вещественное евклидово пространство(скалярное произведение, неравенство Коши-Буняковского, ортонормированный базис, процедура ортогонализации)

Определение. Векторное пространство 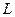с заданным на нем билинейным функционалом 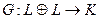называется пространством со скалярным умножением. Значение (число) 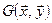функционала 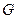на векторе 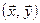будем называть скалярным произведением векторов 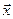, 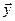и обозначать .

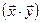Скалярное произведение в общем случае не обладает какой-либо симметрией. Выделим три случая:

1) 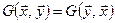. Такие скалярные произведения называются симметричными и задаются симметричными матрицами 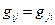, где 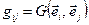. Геометрия пространств с симметричным скалярным произведением называется ортогональной геометрией.

2) 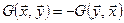. Такие скалярные произведения называются антисимметричными (симплектическими) и задаются антисимметричными матрицами 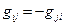. Геометрия пространств с антисимметричным скалярным произведением называется симплектической геометрией.

3) 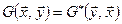. Такие скалярные произведения задаются матрицами, удовлетворяющими свойству 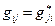, в векторных пространствах, определенных над полем комплексных чисел, и называются эрмитово-симметричными. В качестве примера можно привести скалярное произведение волновых функций в квантовой механике .

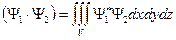Определение. Векторное пространство 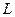с симметричным скалярным умножением, заданное над полем вещественных чисел 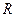, называется евклидовым пространством, если 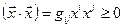, причем равенство 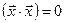имеет место только в случае нулевого вектора .

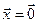Замечание. Квадратичная форма 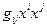, обладающая отмеченным выше свойством, называется положительно определенной квадратичной формой.

В евклидовом пространстве можно ввести норму (длину) вектора правилом .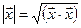

Теорема (неравенство Коши-Буняковского). Для любых двух векторов 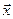и 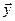евклидового пространства справедливо неравенство

.

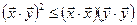Следствие (неравенство треугольника). Для любых двух векторов 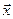и 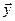евклидового пространства справедливо неравенство

.

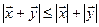Справедливость неравенства Коши-Буняковского для евклидовых пространств позволяет ввести для этих пространств понятие угла 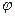между векторами с помощью формулы

.

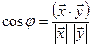В общем случае два вектора пространства 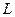со скалярным умножением 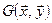называются ортогональными, если их скалярное произведение 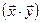равно нулю. В евклидовых пространствах угол между ортогональными векторами равен 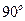(т.е. такие векторы перпендикулярны).

Определение. Будем говорить, что 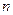элементов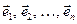 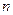-мерного евклидового пространства образует ортонормированный базис этого пространства, если эти элементы попарно ортогональны и норма каждого из этих элементов равна единице, т.е. если .

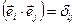Теорема. Во всяком евклидовом пространстве 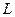существует ортонормированный базис.

Доказательство этой теоремы заключается в построении такого базиса. Пусть 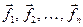- некоторый базис пространства 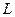. Ортонормированным базисом 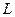будет базис:

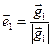, где ;

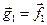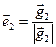, где ;

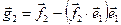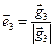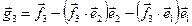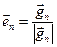, где ;

………………………………………..

, где .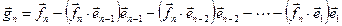

Отметим два основных свойства ортонормированных базисов.

Свойство 1. При использовании ортонормированного базиса скалярное произведение любых двух векторов равно сумме произведений их соответствующих координат.

Действительно, .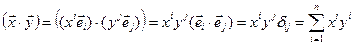

Свойство 2. Координаты произвольного вектора относительно ортонормированного базиса равны скалярным произведениям этого вектора на соответствующие базисные векторы.

Действительно,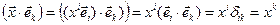

Понятие тензора

Определение. Тензором типа 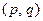валентности 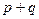называется объект, который задается в некоторой системе координат 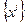набором чисел 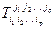, преобразующихся по тензорному закону

,

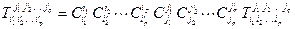при замене системы координат .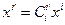

В соответствии с определением вектор 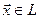является тензором типа 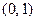, а ковектор 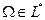- тензором типа 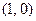. Оба имеют валентность, равную единице.

Можно определить различные операции над тензорами.

1. Сложение тензоров: ( .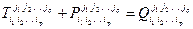

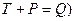2. Умножение тензора на число: ( ).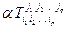

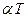3. Свертка тензора: 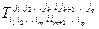(по индексу 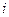проводится суммирование).

4. Тензорное умножение: ( ).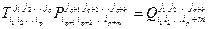

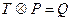Индексы тензора можно поднимать и опускать. Введем метрический тензор 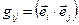. С помощью этого тензора можно опускать индексы: 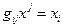. Числа 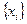называются ковариантными координатами вектора, а числа 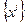- контрвариантными координатами вектора 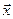. С помощью тензора 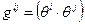индексы тензора можно поднимать: 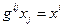. Матрицы 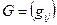и 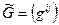связаны соотношением 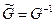(для симметричных скалярных произведений).