Уравнение в полных дифференциалах. Интегрирующий множитель
Обыкновенное дифференциальное уравнение первого порядка вида
P(x, y) dx + Q(x, y) dy = 0
называется уравнением в полных дифференциалах, если P(x, y) и Q(x, y) непрерывны в некоторой односвязной области D и в этой области выполнено условие
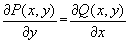
Тогда общий интеграл уравнения задается выражением
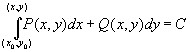 .
.
Обозначим
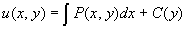
тогда
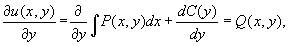
откуда
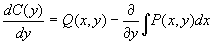
и формула для вычисления u(x, y) имеет вид:
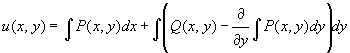
Выражение u(x, y)=0, где
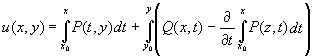
задает решение задачи Коши y(x0) = y0.
Уравнение в полных дифференциалах и их решение
Пусть задано диф. ур-е ел. Вида:
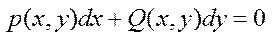
где P(x,y) и Q(x,y) – непрер. Функции имеющие непрерыв часн. Производную 2 порядка включительно.
Диф. ур. Назыв. Ур-ем в полных диф-лах , если 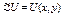 такое что
такое что
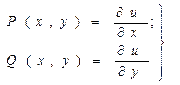
т.е. ур. В этом случае имеет вид : 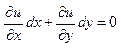
это уравнение явл полным диф. функции U как ф-ции двух переменных:

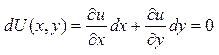
если выполняется равенство тогда то левая часть 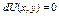 а тогда его решение
а тогда его решение
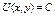 - общий интеграл диф. Ур.
- общий интеграл диф. Ур.
Теорема о необходимости и достаточности условия того что Ур было ур-ем в полных дифференциалах
Теорема : Для того чтобы ур было ур-ем в полных диф. в некоторой Дпринадл ХОУ
Необх. И дост. Чтобы во всех точках обл. Д выполн равенство 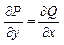 если условие выполняется можно найти ф-цию
если условие выполняется можно найти ф-цию 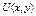 что будет выполняться рав-во след. Образом.
что будет выполняться рав-во след. Образом.
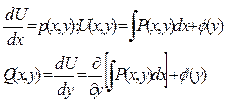
найдем 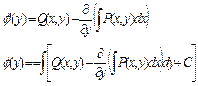
Интегральный множитель и его нахождение
Пусть задано диф. ур-ние в диф. форме вида :
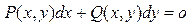
не всякое такое уравнение явл. Уравнением в полных виференциалах однако доказано что для всякого такого ур-я может быть подобрана ф-ция 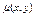 такая что после умножения левого и правого ур-я на эту функцию данное уравнение стан ур-ем в полных диф. Ф-цияю
такая что после умножения левого и правого ур-я на эту функцию данное уравнение стан ур-ем в полных диф. Ф-цияю 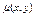 назыв интегральным множителем данного уравнения
назыв интегральным множителем данного уравнения
Найдем функцию определяющую интегр. Множитель данного уравнения:
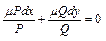
тогда должно выполн. Рав-во:
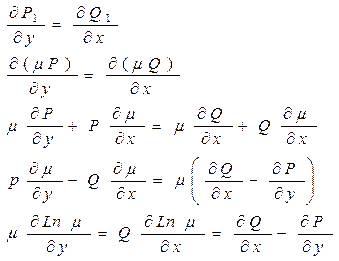
имеем уравнение в частных производных относит неизв функции Мю.Общего метода нахожения которой не существует
Найдем интегр множитель в случае если он явл ф-цией от одной из перемен.
1)Найдем условие при которых 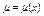 функция
функция 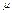 должна удовлетв равенству
должна удовлетв равенству
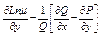 ;
; 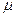 будет зависеть только от Х если правая часть ур будет зависеть только от Х
будет зависеть только от Х если правая часть ур будет зависеть только от Х
2) Аналогично и 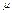 =
= 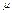 (У)
(У)
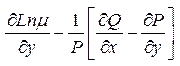 ;
; 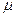 будет зависеть только от Х если правая часть ур будет зависеть только от
будет зависеть только от Х если правая часть ур будет зависеть только от
y
Билет 34.
Дифференциальные уравнения порядка выше 1-го, допускающие понижения порядка.
А)Уравнения вида 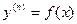 .Общее решение получается путём n-кратного интегрирования
.Общее решение получается путём n-кратного интегрирования 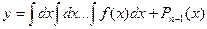 ,где
,где 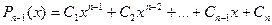 , или по формуле
, или по формуле
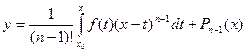
б) 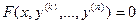 , т.е. уравнения не содержащие явно искомой функции и её производных до порядка (k-1) включительно.С помощью замены переменной
, т.е. уравнения не содержащие явно искомой функции и её производных до порядка (k-1) включительно.С помощью замены переменной 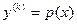 порядок уравнения понижается на k единиц:
порядок уравнения понижается на k единиц: 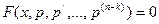 .Предположим , что для полученного уравнения путём N-кратного интегрирования мы можем найти общее решение
.Предположим , что для полученного уравнения путём N-кратного интегрирования мы можем найти общее решение 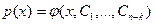 .Тогда искомая функция y(x) получается путём k-кратного интегрирования функции
.Тогда искомая функция y(x) получается путём k-кратного интегрирования функции 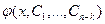 .
.
в) 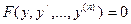 , не содержащие явно зависимой переменной. Подстановкой
, не содержащие явно зависимой переменной. Подстановкой 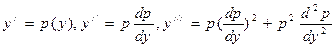 , и т.д. порядок уравнения понижается на единицу.
, и т.д. порядок уравнения понижается на единицу.
г) 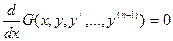 , т.е. такие уравнения , в которых левая часть может быть представлена как полная производная по x от некоторой функции
, т.е. такие уравнения , в которых левая часть может быть представлена как полная производная по x от некоторой функции 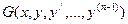 ,.Интегрируя по х , получим новое уравнение, порядок которого на 1 ниже порядка исходного уравнения.
,.Интегрируя по х , получим новое уравнение, порядок которого на 1 ниже порядка исходного уравнения.
д) 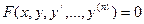 , однородное относительно функции и её производных, т.е. такое, что
, однородное относительно функции и её производных, т.е. такое, что 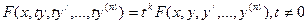 .Подстановкой
.Подстановкой 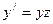 порядок уравнения понижается на 1.
порядок уравнения понижается на 1.
Билет 35.
