Расчет процессов сгорания и расширения методом Гриневецкого – Мазинга

Сгорание

Методика расчёта рабочего цикла ДВС была предложена В.И. Гриневецким и в дальнейшем развита Н.Р. Бриллингом и Е.К. Мазингом. Методика содержит ряд упрощающих допущений:

1. Для циклов двигателей с внутренним смесеобразованием кривая давления при сгорании заменяется изохорно-изобарным сообщением теплоты рабочему телу, а для двигателей с внешним смесеобразованием сообщение тепла принимается изохорным. Участок c-z диаграммы называют периодом видимого сгорания.

2. Начало подвода тепла происходит в момент нахождения поршня в ВМТ.

3. В двигателях с внутренним смесеобразованием часть топлива сгорает при условии V=const, а остальная часть – при условии p= const. Величиной степени повышения давления при изохорном подводе тепла λ= p_z/p_cзадаются на основании опытных данных по двигателям – прототипам.

Помимо этого учитывают тепловые потери и зависимость теплоёмкости от температуры и химического состава рабочего тела.

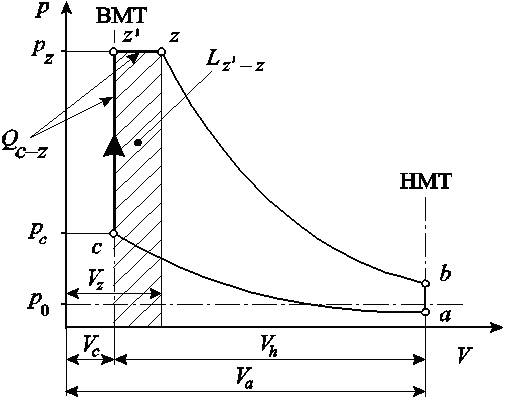
Температуру рабочего тела в результате сгорания топлива можно определить на основании первого закона термодинамики:

Q_cz = U_z – U_c + L_cz(37)

где U_c и U_z – внутренняя энергия рабочего тела в конце процессов сжатия и сгорания; Q_cz – подведенное к рабочему телу в процессах V =const и p = constколичество теплоты; L_cz – работа газов в процессе предварительного расширения z₁–z;

Количество теплоты, выделяемое при сгорании свежего заряда, полученного из 1 кг топлива, можно записать в общем случае как (H_u – ΔH_u). Однако, кроме потерь тепла вследствие химической неполноты сгорания, при сгорании происходит еще целый ряд потерь:

потери тепла вследствие теплообмена со стенками;

потери тепла вследствие диссоциации части продуктов сгорания;

потери, связанные с несовершенством смесеобразования и сгорания, приводящие к выделению части тепла уже на линии расширения.

Это ведет к снижению эффективности использования теплоты и может рассматриваться как тепловые потери.

Все потерянное тепло не идет на изменение внутренней энергии рабочего тела на участке c-zдиаграммы цикла и совершения механической работы на участке c-zдиаграммы цикла и должно быть учтено при использовании уравнения (37).

Вычисление каждой составляющей потерь затруднительно, поэтому при расчетах учет суммарных потерь тепла ведут путем введения коэффициента полноты тепловыделения в период видимого сгорания – ξ_z. Кроме того, ранее был введен коэффициент выделения теплоты χ, учитывающий возможную неполноту сгорания топлива в течение цикла. С учетом всех видов потери тепла в период видимого сгорания количество использованной теплоты может быть выражено как:

Q_cz = ξ χ H_u (38)

Внутренняя энергия рабочей смеси в конце сжатия определится как сумма внутренней энергии свежего заряда и остаточных газов:

U_c = M₁ u_c + M_ru_c^'', (39)

где u_c, u_c^'' – мольная внутренняя энергия свежего заряда и остаточных газов при параметрах точки z диаграммы цикла, соответственно.

В конце периода видимого сгорания внутренняя энергия рабочего тела равна:

U_z = (M₂ + M_r) u_z'' , (40)

где u_z'' – мольная внутренняя энергия продуктов сгорания при параметрах точки z.

Величина ξ_z в дизелях зависит от коэффициента избытка воздуха a и от совершенства организации процессов смесеобразования и сгорания, то есть, от типа камеры сгорания.

Как правило, чем меньше a, тем больше неполнота сгорания и меньше величина ξ_z.

В табл. приведены средние значения ξ_z в зависимости от типа камеры сгорания.

Типы камер сгорания дизелей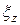
Неразделённые и полуразделённые	0,80…0,85
Разделённые (вихревые и предкамерные)	0,75…0,80

Низшая теплота сгорания дизельных топлив H_u обычно находится в пределах 42…42,7 МДж/кг.

Работа газов в процессе предварительного расширения равна площади заштрихованной части приведенной выше диаграммы цикла:

L_cz = p_zV_z - p_z'V_c = p_zV_z - p_zV_c ,

а т.к. p_z = λp_c , то L_cz = p_zV_z - λp_cV_c ,

λ - степень повышения давления при подводе тепла при постоянном объеме.

Используя уравнение состояния и приняв, что M_z = M₂ + M_r, а M_a = M_c = M₁ + М_r, получаем

p_zV_z = RM_zT_z ,

p_cV_c = R M_aT_c .

После соответствующей подстановки уравнение работы примет вид

L_cz = RM_zT_z - RλM_aT_c (41)

Подставляя все полученные значения слагаемых (38), (39), (40). (41) в исходное уравнение первого закона термодинамики (37), получаем

ξ χ H_u = (M₂ + M_r) u_z'' - (M₁ u_c + M_ru_c^'') + R(M₂ + M_r)T_z – R( M₁ + М_r)T_c,

или, поделив полученное на ( M₁ + М_r) и вспомнив, что

(M₂ + M_r) / (M₁ + М_r) = (μ₀ + γ_r) / (1+ γ_r) = μ ,

μ – коэффициент молекулярного изменения рабочей смеси, после преобразований получим

ξ χ H_u /[M₁ (1+ γ_r)]+(u_c+ γ_r u_c^'')/(1+ γ_r)+RλT_c = μ(u_z''+RT_z) (42)

Задавшись значениями ξ, χиλ, а также вычислив внутреннюю энергию газовой смеси для соответствующих точек цикла с помощью (42) можно вычислить T_z. Вычисления необходимо производитьметодом последовательных приближений, находя такое значение T_z, которое удовлетворяет уравнение (42). Давление при заданном λопределяется из давления конца сжатия, Удельный объем – из уравнения состояния.

Экспериментальные значения l для дизелей с различными камерами сгорания

Тип камеры сгорания	l
Неразделённые (с непосредственным впрыскиванием топлива) и без организованного завихривания воздуха.	1,8…2,2
Полуразделённые с организованными завихриваниями воздуха.	1,6…1,8
Разделённые.	1,4…1,6

При необходимости определения степени предварительного расширения при подводе тепла при постоянном давлении (ρ) можно воспользоваться соотношением λρ = μT_z/T_c .

Параметры рабочего тела в конце сгорания в двигателях с принудительным воспламенением рассчитываются в предположении, что все топливо сгорает при постоянном объеме.

В этом случае работа газов в процессе сгорания равна нулю и уравнение баланса энергии запишется как:

μ u_z'' - u_c/ (1+ γ_r) - u_c^''γ_r / (1+ γ_r) = ξ χ H_u /M₁ (1+ γ_r),

после преобразований получим:

ξ χ H_u /[M₁ (1+ γ_r)] + [(u_c+ γ_r u_c^'')/ (1+ γ_r)] = μ u_z'' (43)

Как и в предыдущем уравнение (43) решается путем подбора удовлетворяющей его температуры. Расчетное давление в конце сгорания определяется с помощью уравнения состояния или из выражения :

λ = μ(T_z /T_c ) и (p_z)_расч = λp_c . (44)

Расчетное давление получено в предположении мгновенного сгорания топлива, оно несколько завышено по отношению к реализуемым на практике давлениям. Это обстоятельство учитывают поправочным коэффициентом φ_р = 0,8 – 0,9, тогда действительное давление определится как:

(p_z)_действ = φ_р (p_z)_расч(46)

Для бензиновых двигателей принимают x_z= 0,85…0,92; для газовых – 0,8…0,85.

Обычно температура рабочего тела в конце изохорного сгорания находится в пределах 2500…2800 К (применительно к режимам полных нагрузок).

Для двигателей с внешним смесеобразованием 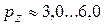МПа

Процесс расширения (описание политропой)

В термодинамическом цикле процесс расширения принят адиабатическим, однако в действительном цикле расширение продуктов сгорания сопровождается теплообменом со стенками, догоранием топлива, рекомбинацией диссоциированных компонентов продуктов сгорания с выделением тепла. Интенсивность этих процессов меняется в течение процесса расширения. Здесь сказывается

Интенсивность теплообмена со стенками зависит от перепада температур и площади открытой поршнем поверхности стенок рабочей камеры. По мере расширения температура рабочего тела снижается, площадь же теплообмена увеличивается. Взаимодействие этих факторов дает сложную картину теплообмена. Однако, в начальной части расширения интенсивность теплообмена и суммарное количество отданного в стенки тепла оказываются больше нежели в заключительной.

Интенсивность догорания и рекомбинации также не постоянны. Догорание быстрее проходит при высоких температурах, т.е. в начале расширения. Рекомбинация заметна лишь при некотором снижении температуры и ускоряется по мере ее снижения. Возможна «закалка». Суммарное тепловыделение максимально в начале расширения и затухает по мере приближения к НМТ. Суммарная теплота, подведенная в процессе расширения Q_zb = (ξ_b – ξ_z)χH_u ,

ξ_b – коэффициент использования теплоты в точке b цикла.

Наиболее простым способом описания процесса расширения является описание его политропой с показателем n₂. Принятое значение показателя должно обеспечить правильные результаты вычислений параметров рабочего тела в конце расширения (точка b индикаторной диаграммы).

Строго говоря, показатель политропы расширения должен быть переменным. В начале расширения в связи с тепловыделением правильное описание кривой расширения дает политропа с показтелем меньше показателя адиабаты (n₂< k₂), далее по мере расширения показатель растет и к концу расширения становится больше показателя адиабаты (n₂> k₂).Здесь сказывается отсутствие тепловыделения и наличие отдачи тепла в стенки. Однако, в связи с трудностью использования переменного показателя как и при расчете процесса сжатия принято использовать политропу с постоянным средним значением показателя.

Тогда параметры рабочего тела в конце расширения для дизеля определятся из уравнения политропы с учетом предварительного расширения как:

p_b = (V_z / V_b)ⁿ²p_z = p_z /δⁿ² (47)

T_b = T_z /δ^n2-1 (48)

Значение δ может быть определено также из соотношения ε=ρδ.

Для бензиновых двигателей с изохорным подводом тепла:

p_b = p_z / εⁿ² (49)

T_b = T_z /ε^n2-1 (50)

Значение принимаемого показателя политропы могут рассчитываться или приниматься из опытных данных. Обычные значения показателя:

для бензиновых двигателей n₂ = 1,22 – 1,28,

для дизелей без наддува n₂ = 1,15 – 1,26.

Показатель адиабаты продуктов сгорания k₂ = 1,3 – 1,33, видим, что средний показатель политропы расширения всегда меньше показателя адиабаты, т.е. догорание и рекомбинация оказывают большее влияние, чем теплоотдача в стенки.

Для правильного выбора значения показателя из приведенных диапазонов необходимо учитывать влияние различных факторов на показатель.

Изменение скорости сгорания. При изменении скорости сгорания при прочих равных условиях изменяется количество топлива успевающего сгореть в период видимого сгорания, т.е. изменяется ξ_z. При уменьшении скорости сгорания уменьшается ξ_z и на линии расширения выделяется большее количество тепла и для учета этого фактора необходимо принимать меньшие значения показателя политропы расширения.

Скоростной режим. С ростом частоты вращения уменьшается время, отводимое на сгорание. В связи с этим увеличивается количество тепла, выделяемого на линии расширения. Далее как в предыдущем.

Размеры цилиндра. При увеличении размера цилиндра уменьшается площадь теплообмена, приходящаяся на единицу массы рабочего тела. что ведет к уменьшению относительных теплопотерь в стенку. Показатель политропы уменьшается.

Влияние наддува. Здесь также уменьшается площадь теплообмена, приходящаяся на единицу массы заряда, уменьшаются относительные теплопотери.

Определение среднего показателя политропы расширения

В отдельных случаях, особенно при расчете двигателей с наддувом, целесообразно определять значение политропы расширения расчетным путем. Это может быть сделано с использованием уравнения первого закона термодинамики, записанного для процесса расширения:

Q_zb = U_b – U_z + L_zb(51)

Ранее было принято, что в процессе расширения также выделяется некоторое количество тепла и это сказывается на протекании расширения, т.е. на значении показателя политропы. С использованием принятых ранее коэффициентов использования тепла ξ_z.и ξ_b.тепловыделение на линии расширения может быть записано как:

Q_zb = (ξ_b – ξ_z)χH_u . (52)

Изменение внутренней энергии продуктов сгорания в процессе расширения является разностью:

U_b – U_z = (M₂ + M_r) u_b'' - (M₂ + M_r) u_z''= (M₂ + M_r) (u_b'' - u_z'') (53)

Работа газов при расширении с использованием уравнения состояния определится как:

L_zb = [1/(n₂ – 1)](P_zV_z – P_bV_b) = (M₂ + M_r)[R/(n₂ – 1)](T_z – T_b) (54)

После подстановки (52), (53), (54) в (51), имея в виду, что

(M₂ + M_r) = M₁ (μ₀ + γ_r), делим полученное выражение на M₁ (μ₀ + γ_r) и получаем далее:

(ξ_b – ξ_z)χH_u /[M₁ (μ₀ + γ_r)] = [R/(n₂ – 1)](T_z – T_b)+ (u_b'' - u_z'') (55)

В этом уравнении 2 неизвестных - T_b и n₂, в качестве второго уравнения для двигателей с принудительным воспламенением или дизелей берутся соответственно

T_b = T_z /ε^n2-1 или T_b = T_z /δ^n2-1 (56)

Уравнения (55) и (56) решаются методом подбора.

Из анализа (55) следует, что показатель политропы расширения зависит от количества подведенной в процессе расширения теплоты, она пропорциональна величине (ξ_b – ξ_z), состава продуктов сгорания и температурных пределов цикла, т.к. от этого зависят значения теплоемкости газовой смеси.

По экспериментальным данным ξ_b = 0,82 – 0,87, в комбинированных двигателях может достигать 0,92.

Расчет процессов сгорания и расширения путем численного решения дифференциальных уравнений

Приведенная выше методика расчета процесса сгорания содержит существенные ограничения. Она не может учитывать продолжительность сгорания, длительность задержки воспламенения, угол задержки воспламенения топлива. Расчет максимального давления цикла двигателей с принудительным воспламенением дает существенно завышенные результаты. Методика не предусматривает возможности использования закона тепловыделения, приближенного к реальным процессам сгорания. Избежать указанных недостатков методики можно лишь путем описания всех важнейших процессов, протекающих при сгорании и расширении дифференциальными уравнениями с последующим численным решением системы дифференциальных уравнений на ЭВМ.

Базовым уравнением системы является уравнение первого закона термодинамики в дифференциальной форме:

dU = dQ_исп – pdV где (57)

dU – изменение внутренней энергии рабочего тела;

dQ_исп – использованная для этого теплота.

Использованная для изменения внутренней энергии теплота является разностью между выделившейся при сгорании теплоты (dQ_выд) и теплотой отданной в стенки в результате теплообмена (dQ_w):

dQ_исп = dQ_выд - dQ_w (58)

Теплоотдача в стенки описывается уравнением Ньютона:

dQ_w = α(Т – Т_ст)F_стdt, здесь

α – коэффициент теплоотдачи;

Т – текущая температура рабочего тела;

Т_ст – температура стенки;

F_ст – площадь открытой поверхности теплообмена;

t – время.

Выделившаяся в результате сгорания топлива за отрезок времени dt теплота может быть определена как

dQ_выд = χH_u dg_T (59)

χ – коэффициент выделения теплоты (полноты сгорания);

dg_T – количество сгоревшего за время dt топлива.

Скорость выделения теплоты определяется производной:

dQ_выд /dt = χH_u dg_T/ dt (60)

Как было принято выше, при сгорании цикловой дозы топлива g_тц выделяется Q_выд.ц теплоты:

Q_выд.ц = χH_u g_тц ,

если поделить правую и левую часть уравнения (60) на количество выделяющейся за цикл теплоты, получим:

dx_выд = dQ_выд/ χH_u g_тц = d(g_T/ g_тц), здесь

x_выд– относительное количество (доля) выделившегося тепла, или доля выгоревшего топлива. Изменение x_выдв течение процесса сгорания называют законом сгорания (или выгорания) топлива. Перед сгоранием доля выгоревшего топлива равна нулю, а в конце сгорания стремится к единице. Закон выгорания может представляться как функцией времени, таки функцией угла поворота коленчатого вала (φ). Также через φ может выражаться и время в приведенных выше уравнениях.

Для адекватного описания процесса сгорания необходимо знание закона выгорания топлива. К настоящему времени разными авторами предложено несколько вариантов описания динамики тепловыделения в ДВС, наиболее часто используется полуэмпирическое уравнение характеристики тепловыделения, предложенное И.И.Вибе.

При выводе этого уравнения автором были использованы качественные представления о скорости химических реакций горения (экспонента) и обработано большое количество опытов с двигателями разных типов. В результате было получена зависимость доли выгоревшего топлива от безразмерного времени или угла поворота коленчатого вала:

x = 1 – exp ln (1 – x_z)(t/t_z)^m+1 ,

t – текущее время;

t_z – длительность полного сгорания;

x_z – доля выгоревшего топлива в конце сгорания.

Аргументом в этом выражении может быть отношение текущего угла ПКВ φ к длительности сгорания, выраженного углом ПКВ φ_z, численные значения отношений будут одинаковыми.

Если принять значение x_z = 0,999, то подставив t_z = t получим коэффициент С = ln (1 – x_z) = 6,908,при значении 0,995 С = 2,996, что дает лучшее совпадение с экспериментальными данными.

Взяв производную по безразмерному времени, получим уравнение безразмерной скорости тепловыделения w₀:

dx/d(t/t_z) = - C(m+1) (t/t_z)^mexpC)(t/t_z)^m+1 = w₀

Задав длительность сгорания по времени или по углу ПКВ и m можно рассчитать кривую тепловыделения. Это выражение универсально по отношению к типу двигателя (цикла). Особенности процесса сгорания учитываются путем выбора значения показателя характера сгорания m , который определяет положение максимума скорости тепловыделения. Чем меньше его значение, тем круче характеристика тепловыделения и тем ближе расположен максимум кривой тепловыделения к началу сгорания.

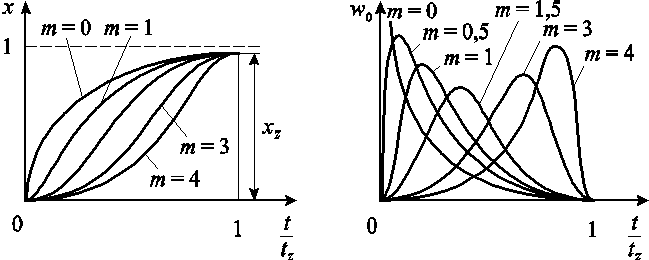
Экспериментальные исследования показали, что для близкого к действительности описания процессов сгорания необходимо принимать следующие значения определяющих величин:

для дизелей m = -0,3….+0,7, φ_z = 60 - 100°ПКВ;

для двигателей с принудительным воспламенением m = 3,0 – 4,0, φ_z = 40 - 60°ПКВ.

Далее приведенные уравнения могут быть расписаны с целью учета текущего состава и свойств рабочего тела, а также расчета выделившегося на каждом расчетном шаге тепла. Возможно, также, введение члена, учитывающего изменение массы участвующего в цикле рабочего тела.

Контрольные вопросы

1. Какие допущения приняты в методике Гриневецкого – Мазинга для расчета процессов сгорания и расширения?

2. Каким образом в методике Гриневецкого – Мазинга учитывается неполнота тепловыделения в период сгорания?

3. Какими тепловыми процессами сопровождается расширение рабочего тела в цилиндре ДВС?

4. Отличается ли значение политропы расширения рабочего тела в цилиндре ДВС от значения показателя адиабаты и почему?

5. Каким образом в методике Гриневецкого – Мазинга для расчета процессов сгорания в дизеле назначается количество тепла, подводимого при постоянном объеме?

6. Каким образом в методике Гриневецкого – Мазинга учитывается количество тепла, выделяющегося при догорании на линии расширения?

7. Каковы основные недостатки методики Гриневецкого – Мазинга?

8. На каких дифференциальных уравнениях базируется методика расчета процессов сгорания и расширения с учетом динамики тепловыделения?

9. Как называется уравнение, которым чаще всего пользуются при расчете динамики тепловыделения?

10. Какие параметры предложены И.И.Вибе для характеристики сгорания в двигателе?