Задачи для самостоятельного решения. 1.Объясните, почему сумма степеней всех вершин простого графа G совпадает с удвоенным

1.Объясните, почему сумма степеней всех вершин простого графа G совпадает с удвоенным числом его ребер. Этот факт называют леммой об эстафете.

Используя эту лемму, покажите, что в любом полном графе К_nс п вершинами есть ровно 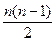ребер. Для каких значений п граф К_nбудет эйлеровым?

2. Опираясь на принцип Дирихле, докажите, что если простой граф G имеет более одной вершины, то у него найдутся по крайней мере две вершины одинаковой степени.

3. Нарисуйте граф, чья матрица смежности имеет вид:

Опишите матрицу смежности полного графа К_n.

4. Введя подходящие обозначения вершин, для каждого из графов на рис. 4.24 подберите соответствующую матрицу смежности из перечисленных ниже.

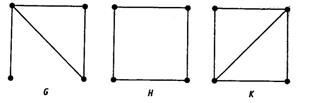
Рис. 4.24.

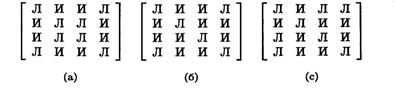
Какие из графов на рис. 4.25 могут являться подграфами графа из упражнения 3?

Рис. 4.25. Кандидаты в подграфы

6.Найдите гамильтоновы циклы в графе на рис. 4.26.

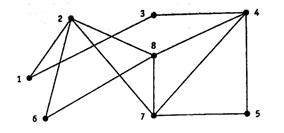
Рис. 4.26.

Найдите в нем циклы длины 3, 4, 5, 6 и 7.

7. На рисунке рис. 4.27 изображен граф Петерсена Р.

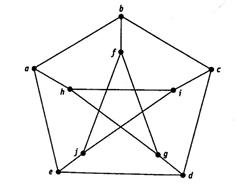Рис. 4.27. Граф Петерсена

Найдите в нем цикл длины 9. Покажите, что Р не является гамильтоновым.

8. Используйте алгоритм ближайшего соседа для поиска гамильтонова цикла в нагруженном графе (рис. 4.28), взяв за исходную

(а) вершину А;

(б) вершину D.

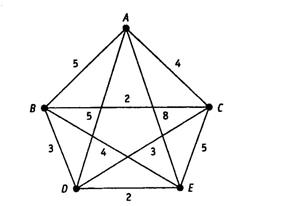Рис. 4.28. Нагруженный граф

9. Выясните, являются ли графы, задаваемые следующими ма­трицами смежности, деревьями:

(а) (б)

10. Известно, что дерево Т имеет три вершины степени 3 и четыре вершины степени 2. Остальные вершины дерева имеют степень 1. Сколько вершин степени 1 есть у дерева Т? (Указание: обозначьте число вершин дерева Т через п и примените лемму об эстафете.)

11. Лесом называют граф (не обязательно связный), каждая компонента связности которого — дерево. Пусть G — лес с п вершинами и kкомпонентами связности.

(а) Докажите, что G имеет п — k ребер.

(б) Покажите, что если в каждой компоненте связности леса G есть более одной вершины, то G содержит по крайней мере 2kвершин степени 1.

(в) Нарисуйте лес с девятью вершинами и шестью ребрами

12.Нарисуйте минимальное остовное дерево графа, изображенного на рис. 4.29.

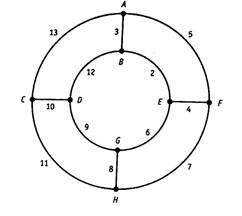Рис. 4.29.

13. В табл. 4.4 приведены расстояния (в милях) между шестью городами Ирландии.

Таблица 4.4

	Атлон	Дублин	Голуэй	Лимерик	Слайго	Уэксфорд
Атлон	-
Дублин		-
Голуэй			-
Лимерик				-
Слайго					-
Уэксфорд						-

Используя алгоритм поиска минимального остовного дерева, найдите сеть дорог минимальной общей длины, связывающую все шесть городов.

14.Глубина вершины v дерева с корнем Т определяется как длина единственного пути от нее к корню дерева. Глубина графа Т — это максимальная глубина его вершин.

(а)Начертите следующие деревья:

(i) дерево с корнем глубины 1 с шестью вершинами;

(ii) полное двоичное дерево с корнем глубины 2;

(iii) дерево с корнем глубины 3, каждая вершина глубины 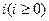которого имеет (i + 1) сына.

(б) Покажите индукцией по n, что полное двоичное дерево с корнем глубины п имеет 2ⁿ листьев.

(полным называется двоичное дерево с корнем, у которого все вершины (за исключением листьев) имеют по два сына).

Основные тезисы

Граф G = (V, Е) состоит из множества V, чьи элементы называют вершинами графа, и множества Е его ребер, соединяющих некоторые пары вершин.

Вершины и и v графа называют смежными,если они соединены каким-то ребром е, про которое говорят, что оно инцидентно вершинам и и v.

Степенью вершины v считают число 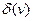ребер графа, инцидентных v (из нее выходящих).

Вершина степени 1 называется висячей. Вершина степени 0 называется изолированной.

Граф, в котором существует маршрут (называемый эйлеровым),начинающийся и заканчивающийся в одной и той же вершине и проходящий по каждому ребру графа ровно один раз, называется Эйлеровым графом. Связный граф с двумя или более вершинами является эйлеровым тогда и только тогда, когда каждая его вершина имеет четную степень.

Ориентированным графом (орграфом) называется тройка G = (V, Е,f), где V – множество вершин графа, Е – множество дуг, а ,f – отображение 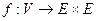, называемое отображением инцидентности.

Ребро е соединяет вершины и и v, а вершины при этом называются концевыми. Ребра, имеющие одинаковые концевые вершины и сами одинаково направленные, называются параллельными (кратными); противоположно направленные ребра – противоположными. Вершина и ребро называют инцидентными друг другу, если вершина является для этого ребра концевой точкой. Две вершины и и v в простом графе называются смежными, если они соединяются каким-то ребром е, про которое говорят, что оно инцидентно вершине и (и v).

Лемма об эстафете утверждает, что сумма степеней вершин произвольного графа G = (У, Е) равна удвоенному числу его ребер.

Простым принято называть граф G = (V, Е) с конечным множеством вершин V и конечным множеством ребер Е, в котором нет петель и кратных ребер.

Логическая матрица отношения на множестве вершин простого графа G, которое задается его ребрами, называется матрицейсмежности.

Подграфомграфа G = (V, Е) называют граф G' = (V',E’), в котором Е' 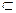Е и 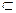V’ V.

Маршрутомдлины k в графе называют такую последовательность различных вершин v₀, v₁ ..., v_k, в которой каждая пара соседних вершин Vi-₁ Vi соединена ребром.

Цикломв графе является замкнутый маршрут v₀, v₁ ..., v₀, у которого все вершины, кроме первой и последней, различны.

Граф, не содержащий циклов, называют ацикличным.

Связнымявляется тот граф, в котором каждая пара вершин соединена маршрутом.

Количество компонент связности графа можно подсчитать с помощью алгоритма связности.

Гамильтоновымназывают такой цикл в графе, который проходит через каждую вершину графа, причем только один раз. Граф, в котором существует гамильтонов цикл, называют гамильтоновым.

Задача коммивояжерасостоит в поиске гамильтонова цикла минимального общего веса в нагруженном графе. Алгоритм ближайшего соседапозволяет найти субоптимальное решение задачи коммивояжера.

Связный ацикличный граф G = (V, Е) является деревом.Следующие утверждения о связном графе G= (V, Е) с п вершинами и требрами эквивалентны:

(а) G — дерево;

(б) любую пару вершин G связывает единственный путь;

(в) G связен и т= п - 1;

(г) G связен, а удаление любого его ребра нарушает это свойство;

(д) G ацикличен, но соединяя любую пару вершин новым ребром, мы получаем цикл.

Остовным деревом графа G называют такой его подграф, который является деревом и содержит все вершины графа G. Алгоритм поиска минимального остовного деревапозволяет найти остовное дерево минимального общего веса в нагруженном графе и может быть использован для решения задачи поиска кратчайшего соединения.

Дерево с одной выделенной вершиной называют деревом с корнем,а выделенную вершину — его корнем.Вершины, стоящие непосредственно под вершиной v (и соединенные с ней ребрами), называются сыновьямивершины v. Вершины, расположенные в самом низу дерева (они не имеют сыновей), называются листьями.Вершины, отличные от корня и листьев, называют внутреннимивершинами графа. Нулевое дерево— это дерево, не имеющее ни одной вершины.

Каждая вершина дерева с корнем Т является корнем какого-то другого дерева, называемого поддеревомТ. Вдвоичном дереве с корнемкаждая вершина имеет не более двух сыновей, а два поддерева вершины v называют левыми правымподдеревьями, ассоциированными с v. Двоичное дерево с корнем называют полным,если каждая его вершина, за исключением листьев, имеет ровно по два сына.

Глубинойвершины v дерева с корнем Т принято считать длину единственного маршрута, соединяющего ее с корнем. Глубиной графаТ называют максимальную глубину его вершин.

Ориентированные графы

Ориентированный граф или орграф представляет собой пару G = (V, Е), где V — конечное множество вершин, а Е — отношение на V. Графическое изображение графа состоит из множества помеченных вершин с ориентированными ребрами (называемых дугами), соединяющими пары вершин. Совокупность всех дуг образует множество Е.

Дугу, соединяющую пару (u, v) вершин uи v орграфа G, будем обозначать через uv. В простом орграфе отсутствуют петли и кратные дуги. Следовательно, для любой пары вершин u и v в орграфе найдется не более одной дуги uv из вершины и в v, и не более одной дуги vu из v в и. Если uv — дуга орграфа, то и называют антецедентом v.

На рис. 4.30 приведен пример простого орграфа с множеством вершин V= {а, Ь, с, d} и множеством дуг Е = {ab, bd, cb, db, dc}.

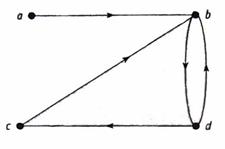
Рис. 4.30. Пример орграфа

Матрицей смежности данного графа служит (несимметричная) матрица:

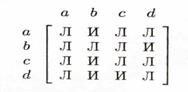
(вершины а, с и d здесь — антецеденты b).

Путем длины k в орграфе называют последовательность различных вершин v₀, v₁, ..., v_k, каждая пара v_i-1v_iкоторой образует дугу (i = 1,...,k). Контуром в орграфе G принято называть последовательность вершин v_0, v₁,... v_k, образующую путь, в которой первая вершина v₀ совпадает с последней v_k , а других повторяющихся вершин в ней нет. Орграф G называют бесконтурным, если в нем нет контуров.

Бесконтурные орграфы полезны в качестве моделей ситуаций, задачи в которых должны выполняться в определенном порядке (контур в такой интерпретации означает, что та или иная задача выполняется с некоторой периодичностью и предшествует сама себе). В задаче о планировании заданий соответствующий бесконтурный орграф имеет кодовое название «система ПЕРТ».

Пример 1.Для получения степени магистра биологии студенту университета, в частности, необходимо прослушать восемь курсов, которые некоторым образом зависят друг от друга. Эта зависимость представлена в табл. 4.5. Изобразите систему ПЕРТ, иллюстрирующую приоритетную структуру курсов.

Таблица 4.5

	Предварительные курсы
(A)	Биотехнология	B
(B)	Начальный курс биотехнологии	C
(C)	Цитология	H
(D)	Структура ДНК	C
(E)	Энзимология	D,G
(F)	Диетология	E
(G)	Генная инженерия	C
(H)	Биология человека	Никаких требований

Решение. Система ПЕРТ (см. рис. 4.31) — это просто орграф, представляющий данную приоритетную структуру. Вершины орграфа в данном случае — восемь курсов. Для краткости ссылок мы обозначим курсы буквами латинского алфавита от А до Н. Дуги орграфа отражают представленные в таблице требования, необходимые для усвоения данного курса.

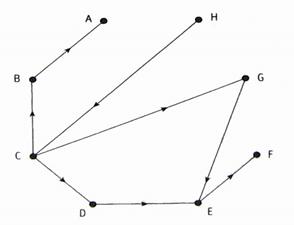
Рис. 4.31 Система ПЕРТ: Приоритетная структура курсов

Предположим, что студент из примера 1 намерен определить порядок, в котором ему следует изучать предметы, учитывая их зависимость друг от друга. Он может сделать это с помощью алгоритма топологической сортировки. Алгоритм создает последовательность согласованных меток для вершин бесконтурного орграфа таким образом, что если 1, 2, 3, ..., п — метки вершин и uv — дуга орграфа, идущая от вершины и с меткой iк вершине v с меткой j, то i < j.