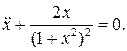Производная в силу системы. Первые интегралы

Рассмотрим систему:

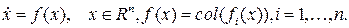(2.1)

Определение 2.1. Функция u(x) называется первым интегралом автономной системы (2.1), если она постоянна вдоль каждой фазовой траектории этой системы, то есть если 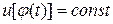для любого решения 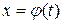системы (2.1).

Теорема. Для того, чтобы функция u(x) была первым интегралом системы (2.1), необходимо и достаточно, чтобы ее производная в силу этой системы тождественно обращалась в нуль, то есть чтобы выполнялось соотношение:

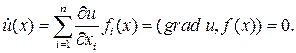(2.2)

Первый интеграл u(x) системы, это некоторый закон сохранения энергии в этой системе. При движении вдоль траекторий системы величина u(x) сохраняет свое первоначальное значение. Именно из этих соображений и были получены первые интегралы многих уравнений классической механики.

Пример 2.1. Одномерное движение материальной частицы массы m в потенциальном поле описывается уравнением Ньютона:

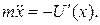(2.3)
Здесь U(x) – потенциал поля. Первый интеграл уравнения (2.3) – функция 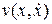, которая постоянна при 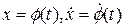, где 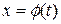– решение этого уравнения.

Для того, чтобы найти первый интеграл, умножим обе части уравнения (2.3) на :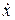

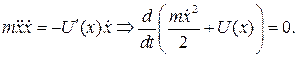
Таким образом, 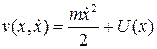и есть первый интеграл уравнения (2.3). Этот интеграл носит название интеграл энергии, поскольку он равен сумме кинетической 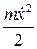и потенциальной U(x) энергии частицы. Как видим, в данном случае сумма кинетической и потенциальной энергии механической системы постоянна:

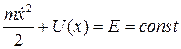, (2.4)

то есть рассеяние энергии отсутствует. Такие системы называют консервативными. Если заданы начальные условия 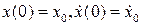, то .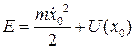

Отметим, что уравнение (2.3) эквивалентно системе

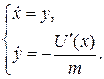(2.5)
Точки покоя системы (2.5) определены соотношениями 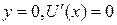, то есть имеют координаты 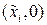, где 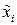– абсциссы точек экстремума функции .

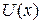Соотношение (2.4) позволяет исследовать и построить фазовый портрет уравнения (2.3) на плоскости 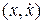(системы (2.5) на плоскости 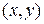), рассматривая ее фазовые траектории как однопараметрическое семейство кривых, где роль параметра играет величина E полной энергии системы.

Пусть, например, график функции U(x), имеет вид, показанный на рис. 2.1. 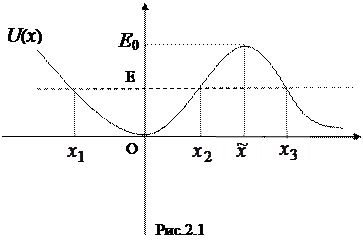Точки О и 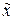соответствуют состояниям равновесия системы (точкам экстремума функции U(x) потенциальной энергии системы).

Построим фазовый портрет системы. Положим 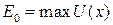= 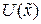. Зададимся некоторым значением 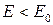. Из (2.4) следует, что 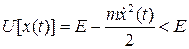вдоль любого решения системы (2.5). Значит траектории этих решений таковы, что 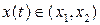или 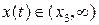. При этом связь между x и 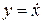определяется соотношением

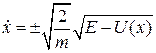. (2.6)

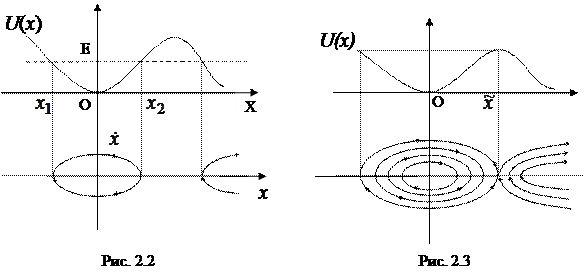Направление движения вдоль траекторий определяется так: при 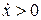(то есть в верхней полуплоскости) x(t) возрастает как функция времени. Соответственно, в нижней полуплоскости она убывает. Для значения E, выбранного так, как указано на рис.2.2, получим две траектории системы (см. рис.2.2). Варьируя значения E, можем схематически построить фазовый портрет системы (2.5) (рис.2..3).

Отметим, что структура траекторий в окрестности точки 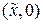такая же, как и в окрестности седла. Кривые «входящие» в указанную особую точку и «выходящие» из нее – сепаратрисы седла. Сепаратрисы разделяют области на фазовой плоскости с различным типом поведения траекторий.

Структура траекторий в окрестности точки (О,О) такая же, как в окрестность центра. Все траектории в указанной окрестности являются замкнутыми траекториями (циклами), что соответствует периодическим движениям системы. Периодическое движение происходит в области 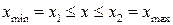, в которой 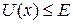, причем равенство достигается на концах интервала, т.е. 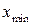и 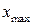представляют собой корни уравнения 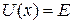. В этом случае мы можем проинтегрировать выражение (2.6) по всей замкнутой фазовой кривой и определить период колебания 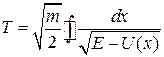. Используя правило вычисления криволинейного интеграла, этому интегралу можно придать вид

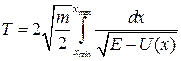. (2.7)

Определение 2.2.Периодические движения системы (2.5) в окрестности точки типа "центр" называются изохронными, если их период не зависит от уровня энергии 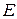и неизохронными в противном случае.

Пример 2.2.Рассмотрим уравнение линейного гармонического осциллятора 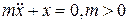. Здесь 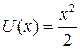. Значения 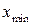и 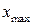находятся из уравнения 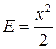, что дает 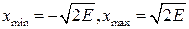. По формуле (2.7) имеем .

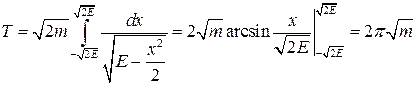Таким образом, период колебаний не зависит от уровня энергии 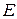и колебания являются изохронными.

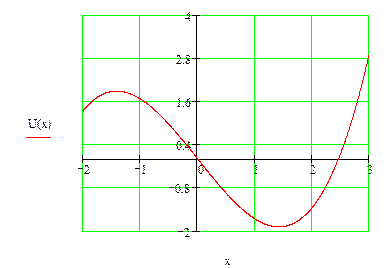
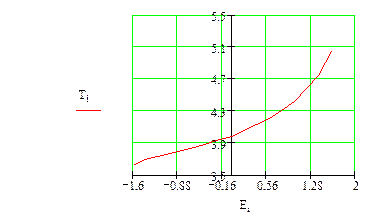
Пример 2.3.Рассмотрим систему с 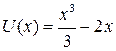. С помощью пакета Mathcad проведем расчет зависимости периода колебаний от уровня энергии

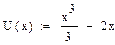
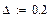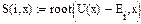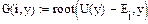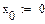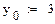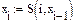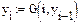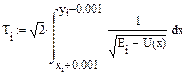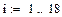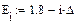Как видим, при увеличении уровня энергии системы от -1,6 до 1,6 период колебаний растет. Значит, движение в рассматриваемом случае не является изохронным.

Замечание.При вычислении интеграла введены поправки в пределы интегрирования для того, чтобы нивелировать погрешность, допускаемую системой Mathcad при подсчете значени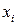й и 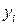. Если этого не сделать, то некоторые значения 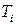оказываются комплексными.

Фазовый портрет системы с 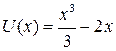представлен на рис. 2.4.

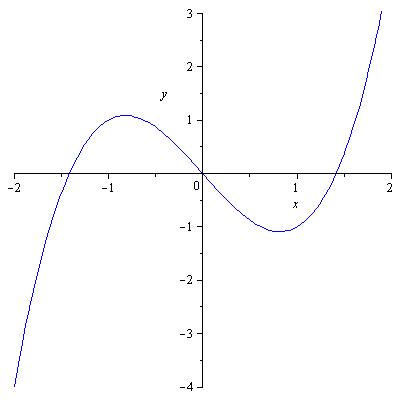
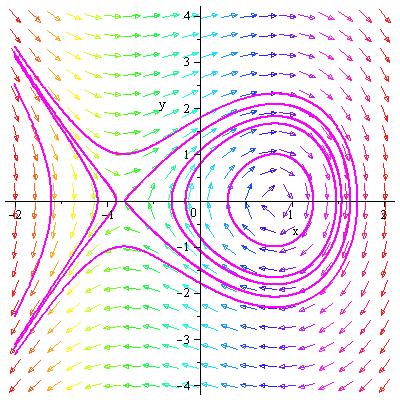
Рис. 2.4

Задание 2

Найдя первый интеграл, изобразить фазовый портрет уравнения на плоскости .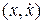

1.

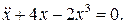
2.

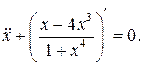
3.

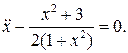
4.

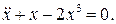
5.

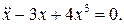
6.

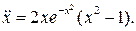
7.

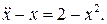
8.

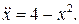
9.

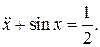
10.

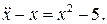
11.

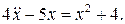
12.

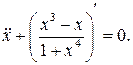
13.

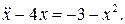
14.

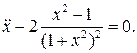
15.

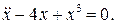
16.

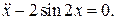
17.

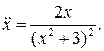
18.

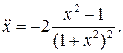
19.

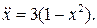
20.

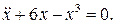
21.

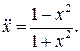
22.

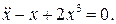
23.

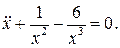
24.

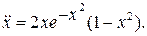
25.

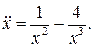
26.

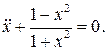
27.

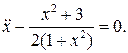
28.

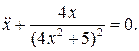
29.

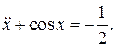
30.

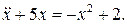
31.