Интервалы возрастания и убывания функции. Исследование на экстремум с помощью первого достаточного условия существования экстремума
САМАРСКИЙ ГОСУДАРСТВЕННЫЙ
АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени академика СП. КОРОЛЕВА
Кафедра высшей математики
Расчетно-графическая работа
Полное исследование функции
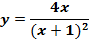
Выполнил: Пугачев Сергей гр. 313
Сдано, дата:
г. Самара
Задание:
1. Указать область определения функции.1
2. Определить чётность-нечетность функции. Указать на особенность графика функции (есть ли симметрия). Найти точки пересечения графика с осями координат.2
3. Найти точки разрыва функции. Указать род точек разрыва. Найти пределы функции при x→+∞, x→-∞.3
4. Найти интервалы возрастания и убывания функции. Исследовать функцию на экстремум с помощью первого достаточного условия.4
5. Найти интервалы выпуклости и вогнутости графика функции, точки перегиба.6
6. Исследовать функцию на экстремум с помощью второго достаточного условия.7
7. Записать уравнения асимптот графика функции.8
8. Построить график функции.9
Область определения функции
Функция 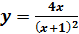
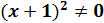 . x≠-1. Таким образом, D(y):x
. x≠-1. Таким образом, D(y):x 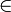 (-∞;-1)∩(-1;+∞).
(-∞;-1)∩(-1;+∞).
Чётность-нечетность функции. Особенности графика функции
f(-x) = 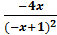 ≠f(x) => f(x) – функция общего вида.
≠f(x) => f(x) – функция общего вида.
Найдем пересечение графика с осью ox:
y=0; 4x=0; x= 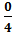 ; x=0.
; x=0.
Найдем пересечение с осью oy:
y=0; y=0.
3. Точки разрыва функции. Род точек разрыва. Пределы функции при x→+∞, x→-∞
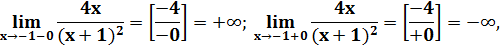
Односторонние пределы не являются конечными, следовательно, x=-1 - точка разрыва второго рода.
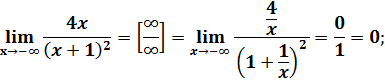
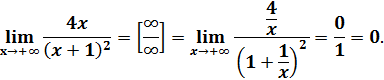
Схематично построим график функции в окрестности точки x=-1 и при x→+∞, x→-∞.
Интервалы возрастания и убывания функции. Исследование на экстремум с помощью первого достаточного условия существования экстремума
Для полного исследования функции найдем первую и вторую производные:
Исследуемая функция: 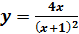 . Производные:
. Производные:
y´= 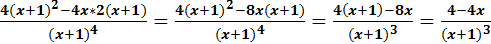 ;
;
y´´= 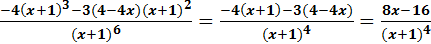 .
.
Таким образом 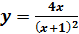 , y´=
, y´= 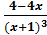 , y´´=
, y´´= 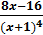 .
.
Найдем критические точки. По определению:
| Критической точкой функции y=f(x) называется внутренняя точка области определения, в которой производная f´(x) равна нулю или не существует. |
В нашем случае производная не существует в точке x=-1. Но эта точка является точкой разрыва и не входит в область определения, поэтому не является критической.
Приравняем производную к нулю: y´= 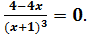
Отсюда 4-4x=0; 1-x=0; x=1. Таким образом: x=1 - критическая точка, x= -1 - точка разрыва функции.
| ДОСТАТОЧНОЕ УСЛОВИЕ ВОЗРАСТАНИЯ, УБЫВАНИЯ ФУНКЦИИ: Если на интервале производная f´(x) положительна, то функция y=f(x) возрастает, если отрицательна, то убывает. |
Знак производной может измениться только в критических точках или в точках разрыва функции.
Покажем знаки производной на числовой оси:
Функция возрастает на интервале: (-1;1].
Функция убывает на интервале: (-∞;-1), (1;+∞).
ПЕРВОЕ ДОСТАТОЧНОЕ УСЛОВИЕ СУЩЕСТВОВАНИЯ ЭКСТРЕМУМА: Пусть функция y=f(x) непрерывна в точке x1 и дифференцируема в окрестности этой точки. Тогда, если при переходе через точку x1 слева направо производная f´(x) меняет знак: 1) с + на -, то в точке x1 максимум; 2)с – на +, то в точке x1 минимум. 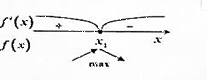 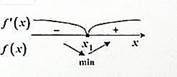 Если производная не меняет знак, то экстремума в этой критической точке нет. Если производная не меняет знак, то экстремума в этой критической точке нет. |
В нашем случае: ymax = f(1)= 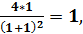
ymin - не существует.
5. Интервалы выпуклости и вогнутости графика функции, точки перегиба
Первая производная функции f´(x) позволяет найти интервалы возрастания и убывания функции y=f(x), а также точки экстремума. Для нахождения интервалов выпуклости и вогнутости графика функции, а также точки перегиба, нужно определить знаки второй производной f´´(x).
| ДОСТАТОЧНОЕ УСЛОВИЕ ВЫПУКЛОСТИ И ВОГНУТОСТИ ГРАФИКА ФУНКЦИИ: Если на интервале вторая производная f´´(x) положительна, то график функции y=f(x) на этом интервале вогнутый. Если на интервале вторая производная f´´(x) отрицательна, то график функции y=f(x) на этом интервале выпуклый. Если вторая производная f´´(x) при переходе через точку c меняет знак, то эта точка является точкой перегиба. При этом в точке с функция должна быть непрерывна. Точка разрыва функции не считается точкой перегиба. |
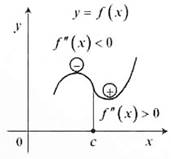 Запомнить это правило можно с помощью рисунка. На шарике показан знак второй производной. Условимся считать, что если график выпуклый, то шарик не устойчив на кривой и на нем должен стоять знак минус. Если график вогнутый, то шарик устойчив на кривой и на нем должен стоять знак плюя. Таким образом, условно установим связь между выпуклостью-вогнутостью и знаком второй производной. Запомнить это правило можно с помощью рисунка. На шарике показан знак второй производной. Условимся считать, что если график выпуклый, то шарик не устойчив на кривой и на нем должен стоять знак минус. Если график вогнутый, то шарик устойчив на кривой и на нем должен стоять знак плюя. Таким образом, условно установим связь между выпуклостью-вогнутостью и знаком второй производной. |
Для исследуемой функции y´´= 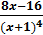 .
.
Знак производной может измениться в точке, где она равна нулю или в точке, где она не существует. В нашем случае уравнение 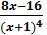 = 0 имеет один корень x=2, следовательно, в точке x=2y´´= 0. Существует y´´ в точке x=-1.
= 0 имеет один корень x=2, следовательно, в точке x=2y´´= 0. Существует y´´ в точке x=-1.

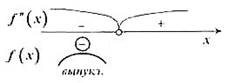 График функции выпуклый на интервале (-∞;-1)∩(-1;+∞). Точка x=-1 на графике функции y=f(x) является точкой разрыва, поэтому не считается точкой перегиба.
График функции выпуклый на интервале (-∞;-1)∩(-1;+∞). Точка x=-1 на графике функции y=f(x) является точкой разрыва, поэтому не считается точкой перегиба.
