Угол между плоскостями

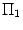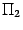Пусть плоскости и заданы соответственно уравнениям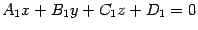и и 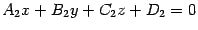. Требуется найти угол 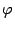между этими плоскостями.

Плоскости, пересекаясь, образуют четыре двугранных угла (рис. 11.6): два тупых и два острых или четыре прямых, причем оба тупых угла равны между собой, и оба острых тоже равны между собой. Мы всегда будем искать острый угол. Для определения его величины возьмем точку 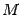на линии пересечения плоскостей и в этой точке в каждой из плоскостей проведем перпендикуляры 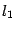и 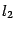к линии пересечения. 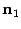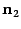Нарисуем также нормальные векторы и плоскосте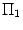й и 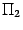с началами в точке 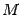(рис. 11.6).

Рис.11.6.Угол между плоскостями

Если через точку 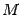провести плоскость 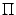, перпендикулярную линии пересечения плоскосте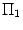й и 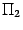, то прямые 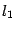и 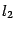и изображения векторов 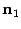и 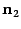будут лежать в этой плоскости. Сделаем чертеж в плоскости 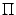(возможны два варианта: рис. 11.7 и 11.8).

Рис.11.7.Угол между нормальными векторами острый

Рис.11.8.Угол между нормальными векторами тупой

В одном варианте (рис. 11.7) 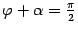и 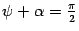, следовательно, угол 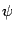между нормальными векторами равен углу 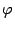, являющемуся линейным углом острого двугранного угла между плоскостям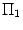и и .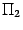

Во втором варианте (рис. 11.8) 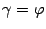, а угол 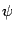между нормальными векторами равен 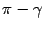. Так как

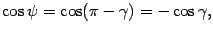
то в обоих случаях .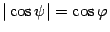

По определению скалярного произведения 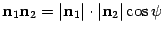. Откуда

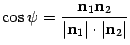
и соответственно

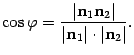(11.4)

Так как координаты нормальных векторов известны, если заданы уравнения плоскостей, то полученная формула (11.4) позволяет найти косинус острого угла между плоскостями.

Если плоскости перпендикулярны, то перпендикулярны и их нормальные векторы. Получаем условие перпендикулярности плоскостей:

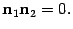(11.5)

Если плоскости параллельны, то коллинеарны их нормальные векторы. Получаем условие параллельности плоскостей

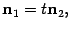(11.6)

где 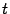-- любое число.

Условие параллельности двух плоскостей.

Две плоскости α₁ и α₂ параллельны тогда и только тогда, когда их нормальные векторы 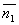и 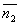параллельны, а значит .

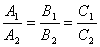Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:

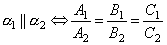или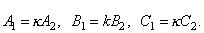

Условие перпендикулярности плоскостей.

Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, 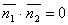или .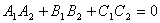

Таким образом, .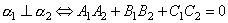

28.

Параметрическое уравнение прямой в пространстве

Параметрические уравнения прямой могут быть записаны следующим образом

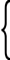	x = l t +x0
y = m t + y0
z = n t + z0

где (x₀, y₀, z₀) - координаты точки лежащей на прямой,

{l; m; n} - координаты направляющего вектора прямой.