Тема ПРОИЗВОДНАЯ ФУНКЦИИ
- Основные понятия
- Таблица производных
- Производная сложной функции
4. Производная произведения и частного
5. Производная тригонометрических функций
6. Производные показательной и логарифмической функций
7. Логарифмическое дифференцирование
8. Дифференцирование функций, заданных неявно
Дифференцирование функций, заданных параметрически
9. Понятие о производных высших порядков
С производной мы сталкиваемся в тех случаях, когда нужно определить скорость изменения одной величины (функции) в зависимости от изменения другой величины (независимой переменной). Например, скорость охлаждения тела, скорость химической реакции и т.д.
Производной функции у =f(x) называется предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю, если этот предел существует: 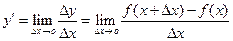 .
.
Обозначают: у′ , f′(x), 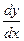 ;
; 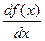 .
.
Производная у′ представляет собой скорость изменения функции у относительно аргумента х в точке х.
Нахождение производной функции называется дифференцированием этой функции.
Геометрический смысл производной: производная f′(xо), есть угловой коэффициент (тангенс угла наклона) касательной, проведенной к кривой у=f(x), в точке хо, т.е. k=f′(xо).
Механический смысл производной: производная пути по времени S′(to) есть скорость точки в момент to: v(to)=S′(to).
Задача 1. Найти производную функции 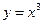 .
.
Решение. 1). Дадим аргументу х приращение 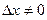 и найдем наращенное значение функции
и найдем наращенное значение функции 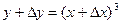 ;
;
2) Приращение функции:
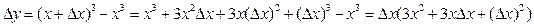 ;
;
3) Составляем отношение 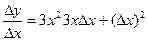 ;
;
4). Находим предел 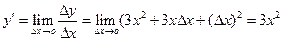 .
.
Задача 2. Найти производную функции 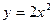 при х=2.
при х=2.
Решение. 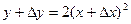 ;
;
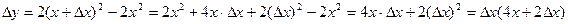 ;
;
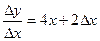 ;
; 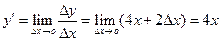 .
.
При х=2 значение производной 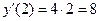 .
.
Можем сказать, что число 8 есть скорость изменения функции 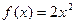 при х=2. Найдя производную
при х=2. Найдя производную 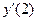 , мы нашли и тангенс угла наклона касательной к графику функции
, мы нашли и тангенс угла наклона касательной к графику функции 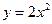 в точке с абсциссой х=2 к оси 0х.
в точке с абсциссой х=2 к оси 0х.
Эту же задачу можно решить так: т.к. 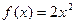 ,
, 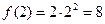 .
.
Перейдем от значения х=2 к значению 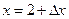 :
: 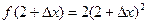 ;
;
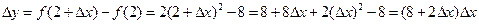 ;
;
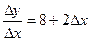 ;
; 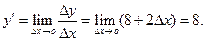
(Здесь мы нашли значение производной данной функции при х=2, минуя нахождение производной, как функции х ).
Задача 3. Точка движется по прямой по закону 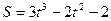 . (S - путь, измеряется в см., t – время в секундах). Найти среднюю скорость точки за время от t=2с до
. (S - путь, измеряется в см., t – время в секундах). Найти среднюю скорость точки за время от t=2с до 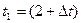 с, считая, что
с, считая, что 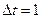 ; 0,5; 0,01; 0,001. Вычислить скорость точки в момент t=2с.
; 0,5; 0,01; 0,001. Вычислить скорость точки в момент t=2с.
Решение. vср= 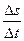 .
.
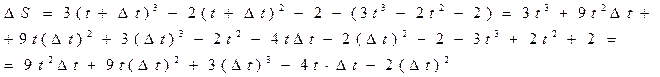 vср=
vср= 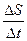 =
= 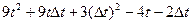 ,
,
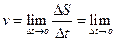
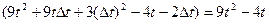 .
.
При t=2с, 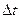 =1с: vср=
=1с: vср= 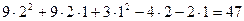 (см/с);
(см/с);
t=2с, 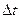 =0,5с: vср=
=0,5с: vср= 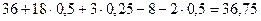 (см/с);
(см/с);
t=2с, 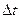 =0,01с: vср=
=0,01с: vср= 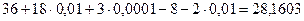 (см/с);
(см/с);
t=3с, 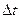 =0,001с: vср=
=0,001с: vср= 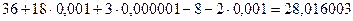 (см./сек.);
(см./сек.);
v(2)= 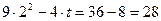 .
.
Мы видим, что чем меньше 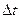 , тем ближе значение средней скорости к истинной скорости в момент t=2с.
, тем ближе значение средней скорости к истинной скорости в момент t=2с.
2. Точка движется по прямой по закону 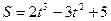 . Найти среднюю скорость за промежуток времени от
. Найти среднюю скорость за промежуток времени от 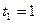 до
до 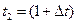 , где
, где 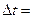 0,5; 0,3; 0,1. Определить скорость в момент t=1с. (S измеряется в сантиметрах, t - секундах).
0,5; 0,3; 0,1. Определить скорость в момент t=1с. (S измеряется в сантиметрах, t - секундах).
В дальнейшем вычислять производные функций мы будем по формулам, которые выводятся исходя из определения производной.
1. Производная постоянной равна нулю, т.е. 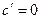 .
.
2. Производная аргумента равна 1, т.е. 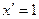 .
.
3. Постоянный множитель можно выносить за знак производной: 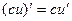 .
.
4. 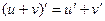 (верно для любого конечного числа дифференцируемых функций),
(верно для любого конечного числа дифференцируемых функций),
5. 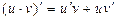 ,
,
6. 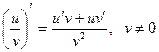 .
.
Таблица производных:
1. 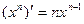 9.
9. 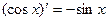
2. 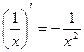 10.
10. 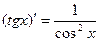
3. 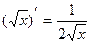 11.
11. 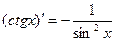
4. 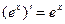 12.
12. 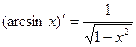
5. 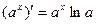 13.
13. 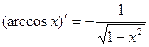
6. 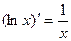 14.
14. 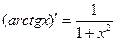
7. 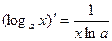 15.
15. 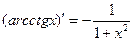
8. 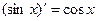
Найти производные функций:
1) 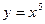 .
.
Воспользуемся формулой (1) из таблицы: 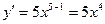 .
.
2) 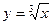 .
.
Если функция имеет иррациональность, рекомендуется переписать ее с дробным показателем степени.
Перепишем в виде: 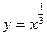 , тогда
, тогда 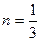 и учитывая (1):
и учитывая (1):
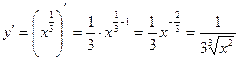 .
.
3) 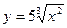 .
.
Перепишем: 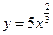 , воспользуемся формулой (1) и тем, что постоянный множитель можно выносить за знак производной:
, воспользуемся формулой (1) и тем, что постоянный множитель можно выносить за знак производной:
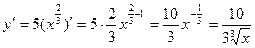 .
.
4) 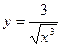 .
.
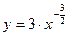 ;
; 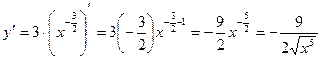 .
.
5) 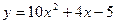
Мы имеем алгебраическую сумму нескольких функций. 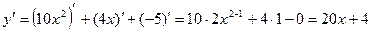 .
.
6) 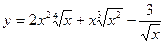 .
.
Перепишем: 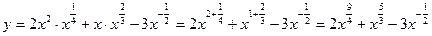 .
.
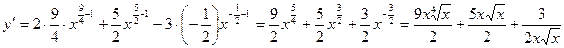 .
.
