Неустановившегося течения жидкости

Таких уравнений два. Первое из них - уравнение неразрывности потока, выражающее закон сохранения массы транспортируемой жидкости (рис.12.5).

x

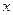
Рис. 12.5. К выводу уравнений неустановившегося течения жидкости

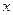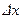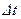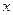Рассмотрим два близко расположенные сечения и трубопровода. Тогда закон сохранения массы жидкости можно сформулировать следующим образом: изменение массы жидкости в области между рассматриваемыми сечениями за время равно разности масс жидкости - , втекающей через сечение , и , вытекающей через сечение . Таким образом, имеем уравнение:

,

в котором нижний индекс показывает, в каком сечении берутся соответствующие параметры течения.

Поскольку с точностью до малых высшего порядка имеет место равенство

,

получаем первое дифференциальное уравнение:

, (12.9)

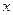где ; ; неизвестные функции и .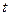

Для установившегося течения частная производная по времени в уравнении (12.9) равна нулю, поэтому из него следует: , т.е. массовый расход жидкости постоянен по длине трубопровода.

Уравнение (12.9) называется уравнением неразрывности.

Второе уравнение, называемое уравнением движенияжидкости, выражает второй закон Ньютона. Для удобства его можно сформулировать так: изменение количества движения любого фиксированного элемента жидкости за время 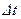, равно суммарному импульсу всех внешних сил, действующих на этот элемент. В качестве элемента жидкости возьмем жидкость, заключенную в момент времени 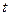между сечениям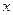и и трубопровода. Учитывая, что этот элемент в момент времени займет новое положение, изменение его количества движения можно записать в следующем виде:

.

Первый член в правой части равенства дает изменение за время 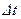количества движения элемента, как если бы он был неподвижен, а два другие члена учитывают движения элемента в трубопроводе: добавляется количество движения частиц, ушедших из рассматриваемого элемента через сечение , и вычитается количество движения частиц, пришедших в рассматриваемый элемент через сечение .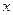

Таким образом, с точностью до малых высшего порядка малости можно написать:

.

Проекция суммарного импульса всех внешних сил, действующих на жидкость в рассматриваемом элементе, на ось трубопровода включает следующие слагаемые:

· импульс сил давления на торцах элемента;

· импульс сил реакции стенок трубопровода;

· импульс сил трения жидкости о внутреннюю поверхность трубопровода;

· импульс сил тяжести, где угол наклона оси трубопровода к горизонту: .

Таким образом, второй закон Ньютона можно представить в следующем виде:

или

. (12.10)

Выполнив дифференцирование произведений в левой части уравнения (12.10), получим

В силу уравнения неразрывности (12.9) первое слагаемое в правой части уравнения равно 0, поэтому имеем:

или

(12.11)

Система уравнений (12.9-12.10) или (12.9-12.11) служит основой для описания неустановившихся течений жидкости в трубопроводе.

Упрощающие допущения

При рассмотрении нестационарных течений многих капельных жидкостей (например, нефтей, нефтепродуктов, воды и т.п.), обычно принимаются следующие допущения и делаются следующие упрощения.

· нефть считается слабо сжимаемой жидкостью, т.е. в уравнении состояния считается, что , поэтому во всех коэффициентах плотность нефти заменяется ее невозмущенным значением;

· считается, что площадь сечения стального нефтепровода изменяется под воздействием давления крайне незначительно, т.е. , поэтому во всех коэффициентах площадь сечения трубопровода заменяется ее невозмущенным значением;

· изменениями величины скоростного напора пренебрегают по сравнению с изменениями пьезометрического напора: ;

· принимается, что скорость течения жидкости в трубопроводе много меньше скорости распространения волн давления;

· принимается так называемая гипотеза квазистационарности трения, согласно которой , представленное формулой , где коэффициент трения (или множитель Фанинга), выражается через коэффициент 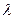гидравлического сопротивления:

(т.е. ),

причем для коэффициента 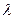используются зависимости, справедливые для стационарного течения.

Основные уравнения

С учетом сделанных допущений уравнение (12.8) преобразуется к виду:

.

Учитывая формулы (12.2), (12.4), согласно которым

и ,

получаем уравнение

, где .

Можно показать, что из условия следует, что . Тогда уравнение неразрывности получает окончательную форму:

. (12.12)

Уравнение (12.11) также упрощается и принимает вид:

. (12.13)

Таким образом, мы приходим к основной системе двух дифференциальных уравнений (12.12) и (12.13) с частными производными, используемых для расчета двух неизвестных функций и .

(12.14)

где .

Если учесть, что ; и , то систему уравнений, определяющих нестационарное течение нефти в трубопроводе, можно записать в терминах объемного расхода и напора :

(12.15)