Распределение случайных величин
В теории вероятностей под распределением случайной величины понимают соответствие между возможными значениями случайной величины и их вероятностями или, в статистике, между наблюдаемыми величинами и их частотами.
Распределение, когда на центральную часть значений приходятся наибольшие частоты, а на крайние значение – меньшие частоты принято называть нормальным. график такой случайной величины выглядит следующим образом:
Надо знать, что кроме нормального распределения случайных величин есть также другие виды, подробнее о них можно узнать в литературе по математической статистике: биномиальное, пуассоновское, показательное, равномерное и др.
Пример 1. Дана таблица распределения веса почтовых отправлений за текущий месяц.
Найти математическое ожидание, дисперсию, среднеквадратичное отклонение, моду и медиану данной случайной величины:
| Интервалы ∆i | (6; 10) | (10; 14) | (14; 18) | (18; 22) | (22; 26) | (26; 30) | (30; 34) | (34; 38) |
| Частоты ni |
Объем выборки, по которой построен статистический ряд, равен n = 4+15+38+58+50+26+8+1= 200 - получают суммированием частот из второй строки таблицы. Относительные частоты вычисляем по формуле
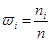
| Интервалы ∆i | (6; 10) | (10; 14) | (14; 18) | (18; 22) | (22; 26) | (26; 30) | (30; 34) | (34; 38) |
| Частоты ni | ||||||||
| Относ.част. ωi | 0,02 | 0,075 | 0,19 | 0,29 | 0,25 | 0,13 | 0,04 | 0,005 |
| Середины xi* |
Сумма относительных частот должна равняться единице. Для построения гистограммы надо над каждым интервалом статистического ряда построить прямоугольник, площадь которого равна соответствующей относительной частоте. Высоты этих прямоугольников определяем по формуле 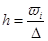 , где ∆=4 длина интервала в статистической таблице. С точностью до третьего знака после запятой получаем: h1=0,005, h2=0,019, h3=0,048, h4=0,068, h5=0,073, h6=0,032, h7=0,01, h8=0,001. .
, где ∆=4 длина интервала в статистической таблице. С точностью до третьего знака после запятой получаем: h1=0,005, h2=0,019, h3=0,048, h4=0,068, h5=0,073, h6=0,032, h7=0,01, h8=0,001. .
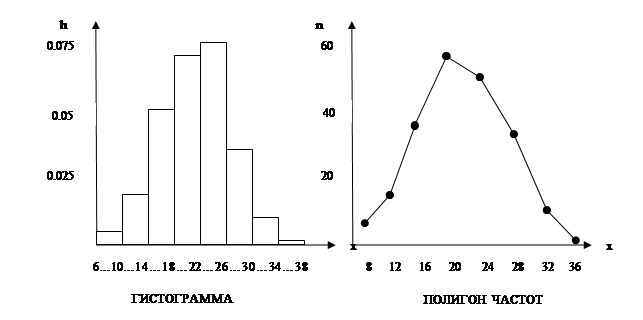
Для построения полигона частот найдем середины каждого из интервалов и отметим частоту для каждого из значений. Соединим их ломаной линией.
Модой данной величины будет интервал 18 – 22 (т.к. таких посылок было отправлено больше всего).
Медиана – лежит также в интервале 18-22 (т.к. это находится посередине выборки. И если разделить все посылки (200 шт.) пополам, граница между половинками будет именно в интервале 18-22
Для расчета математического ожидания, найдем вероятности появления почтовых отправлений (которые соответствуют относительным частотам). Всего было отправлено, значит:
| Относ.част. ωi | 0,02 | 0,075 | 0,19 | 0,29 | 0,25 | 0,13 | 0,04 | 0,005 |
| Середины xi* |

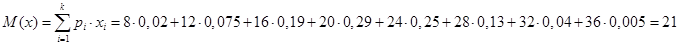
Основные численные методы
Для некоторых подынтегральных функций 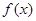 интеграл можно вычислить аналитически, найти в справочниках или оценить с помощью асимптотических рядов. Однако в общем случае
интеграл можно вычислить аналитически, найти в справочниках или оценить с помощью асимптотических рядов. Однако в общем случае 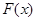 может быть не определена: либо первообразные не выражаются через элементарные функции, либо сами подынтегральные функции не являются элементарными. Это приводит к необходимости разработки приближенных методов вычисления определенных интегралов.
может быть не определена: либо первообразные не выражаются через элементарные функции, либо сами подынтегральные функции не являются элементарными. Это приводит к необходимости разработки приближенных методов вычисления определенных интегралов.
