Производные неявной функции

Если 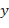есть неявная функция от 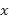, т.е. задана уравнением 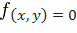, не разрешенным относительно 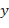, то для нахождения производной 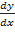нужно продифференцировать по 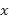обе части равенства, помня, что 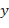есть функция от 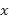, и затем разрешить полученное равенство относительно искомой производной. Как правило, она будет зависеть от 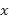и ; .

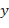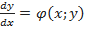Пример №12: Для данных неявных функций найти производные указанного порядка:

a) , ;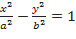

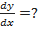b) , ;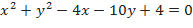

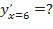c) , .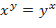

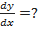Решение:

a) Дифференцируем по 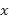обе части равенства, где 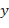есть функция от 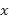, получим: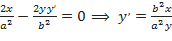

b) Дифференцируя по 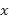, получим: 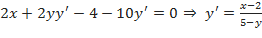. Подставляя заданное значение 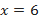в исходное уравнение, найдём два соответствующих ему значения 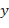: 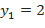, 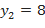. Поэтому при 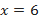и производная 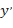имеет два значения: ; .

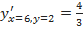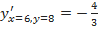c) Прологарифмируем обе части данного уравнения (по основанию 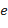), затем дифференцируем по 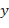, рассматривая 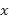как функцию : ; ;
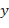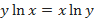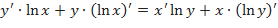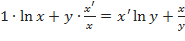. Отсюда найдём .

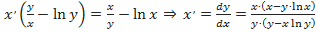Задания:

1) , ;

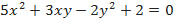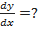2) , ;

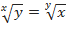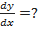3) , .

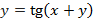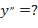Касательная и нормаль к плоской кривой.
Угол между двумя кривыми.

Если плоская кривая отнесена к прямоугольной системе координат, то уравнения касательной и нормали к ней в точке 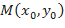имеют вид: ; ,

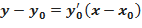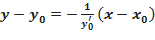где 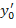- значение в точке 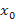производной 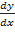из уравнений кривой.

Направление кривой в каждой её точке определяется направлением касательной к ней в этой точке. Угол между двумя пересекающимися кривыми определяется как угол между двумя прямыми, касательными к кривым в точке их пересечения по формуле:

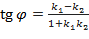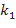, где и 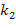- угловые коэффициенты касательных к кривым в точке их пересечения 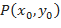, т.е. частные значения в точке 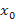производных от 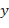по 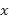из уравнений этих кривых: ; .

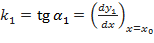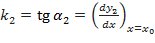Задания: Составить уравнения касательной и нормали:

1) к параболе 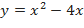в точке, где ;

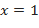2) к окружности 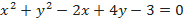в точках пересечения её с осью .

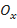Дифференциал функции.

Из определений производной 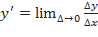и предела переменной следует, что 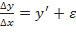, или .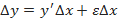

Главная часть приращения функции, линейная относительно приращения независимой переменной, называется дифференциалом функции и обозначается знаком : .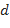

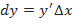Дифференциал независимой переменной 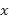равен её приращению, 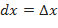, поэтому 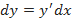, т.е. дифференциал функции равен её производной, умноженной на дифференциал независимой переменной.

Пример№13. Найти полное приращение функции 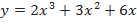и её дифференциал, сравнить их значения при .

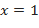Решение:Полное приращение запишем в виде:

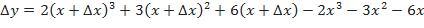
Преобразовав его, получим:

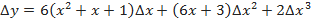
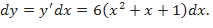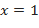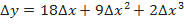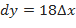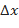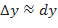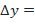
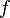
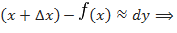
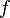
Найдём полный дифференциал. По определению он равен В точке имеем , . При достаточно малых полное приращение функции и дифференциал отличаются незначительно, т.е. . Это обстоятельство используется для приближенных вычислени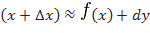й: , или .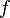

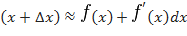Пример№14:Найти приближенное значение .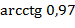

Решение: Представим 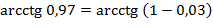, тогда , : .

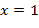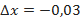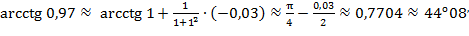Задания:1)Найти дифференциал функций:

a) ;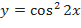

b) ;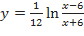

c) .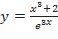

2) Вычислить приближенное значение:

a) 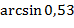; b). .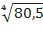

Определение 4.10. Дифференциалом второго порядка называется дифференциал 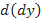, обозначается 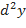. Тогда .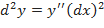