Теоретическое обоснование. Моментом силы относительно точки называется взятое со знаком плюс или минус
Моментом силы относительно точки называется взятое со знаком плюс или минус произведение модуля силы на плечо.
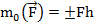
Чтобы определить знак момента необходимо мысленно закрыть пальцем точку, взять за стрелку силы, дернуть по направлению силы и повернуть стрелку вокруг точки: по часовой стрелки – плюс, против - минус.
Из определения следует:
1. момент силы 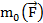 относительно данной точки изменится при переносе силы по линии своего действия;
относительно данной точки изменится при переносе силы по линии своего действия;
2. момент силы 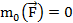 обращается в ноль, когда линия действия силы проходит через эту точку. (Почему? Потому, что
обращается в ноль, когда линия действия силы проходит через эту точку. (Почему? Потому, что 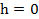 );
);
3. 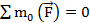 ; сумма моментов двух равных по модулю сил, направленных по одной прямой в противоположные стороны, относительно данной точки равна нулю.
; сумма моментов двух равных по модулю сил, направленных по одной прямой в противоположные стороны, относительно данной точки равна нулю.
Для равновесия плоской системы произвольно расположенных сил, необходимо и достаточно, чтобы алгебраическая сумма проекций сил плоской системы на каждую из координатных осей равнялась нулю, а также алгебраическая сумма моментов сил относительно произвольно выбранной точки центра приведения также равнялась нулю.
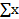 = 0
= 0
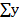 = 0
= 0
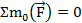
Наложенные на тело связи следует заменить реакциями (т.е. силами действия связей на тело):
· 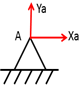 реакцию шарнирно-неподвижной опоры принято представлять в виде двух составляющих реакций по осям координат
реакцию шарнирно-неподвижной опоры принято представлять в виде двух составляющих реакций по осям координат

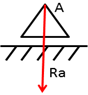
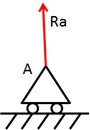
 реакция шарнирно-подвижной опоры направлена по нормали к опорной поверхности шарнира
реакция шарнирно-подвижной опоры направлена по нормали к опорной поверхности шарнира
· реакция точечной опоры (ребро угла) направлена по нормали к гладкой поверхности опирающего тела.в сторону от тела. Гибкая связь, перекинутая через блок, изменяет направление передаваемой силы без изменения ее величины
·  реакция жесткого прямого стержня с шарнирным закреплением концов направлена вдоль его оси в сторону от тела (если стержень воспринимает растягивающую силу) или в сторону к телу (если эта сила сжимающая)
реакция жесткого прямого стержня с шарнирным закреплением концов направлена вдоль его оси в сторону от тела (если стержень воспринимает растягивающую силу) или в сторону к телу (если эта сила сжимающая)

· реакция гладкой опорной поверхности направлена по нормали к этой поверхности в сторону к телу
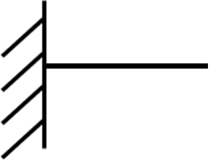
· 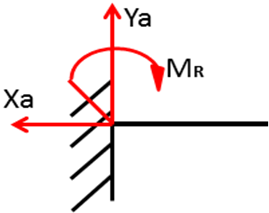 реакция в заделе - помимо двух составляющих реакций по осям координат, возникает реактивный момент
реакция в заделе - помимо двух составляющих реакций по осям координат, возникает реактивный момент
Виды нагрузок: сосредоточенная сила 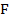 , равномерно распределенная нагрузка интенсивность
, равномерно распределенная нагрузка интенсивность 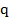 , сосредоточенная пара сил с моментом
, сосредоточенная пара сил с моментом 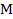 (или просто момент). Интенсивностью распределенной нагрузки называется величина нагрузки, приходящаяся на единицу длины балки. Если по длине балки интенсивность остается постоянной, то распределенная нагрузка называется равномерной. Ее равнодействующая по модулю равна произведению интенсивности нагрузки на длину участка действия и приложена в ее середине.
(или просто момент). Интенсивностью распределенной нагрузки называется величина нагрузки, приходящаяся на единицу длины балки. Если по длине балки интенсивность остается постоянной, то распределенная нагрузка называется равномерной. Ее равнодействующая по модулю равна произведению интенсивности нагрузки на длину участка действия и приложена в ее середине.
ЗАДАНИЕ
ЗАДАЧА
Вариант А Определить реакции опор балки Принять: 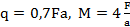 ; для четных вариантов - а=0,6м; для нечетных вариантов – а=0,5м. ; для четных вариантов - а=0,6м; для нечетных вариантов – а=0,5м. | Вариант Б Брус АВ, шарнирно закрепленный в точке А, имеет вторую опору в точке D. Сила тяжести. G бруса приложена в точке С. К свободному концу В бруса прикреплена перекинутая через блок нить, несущая груз F. Определить реакцию шарнира А и опоры D. Принять: 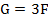 |
| вар | № схемы | F (Н) | вар | № схемы | F (Н) | вар | № схемы | F (Н) | вар | № схемы | F (Н) |
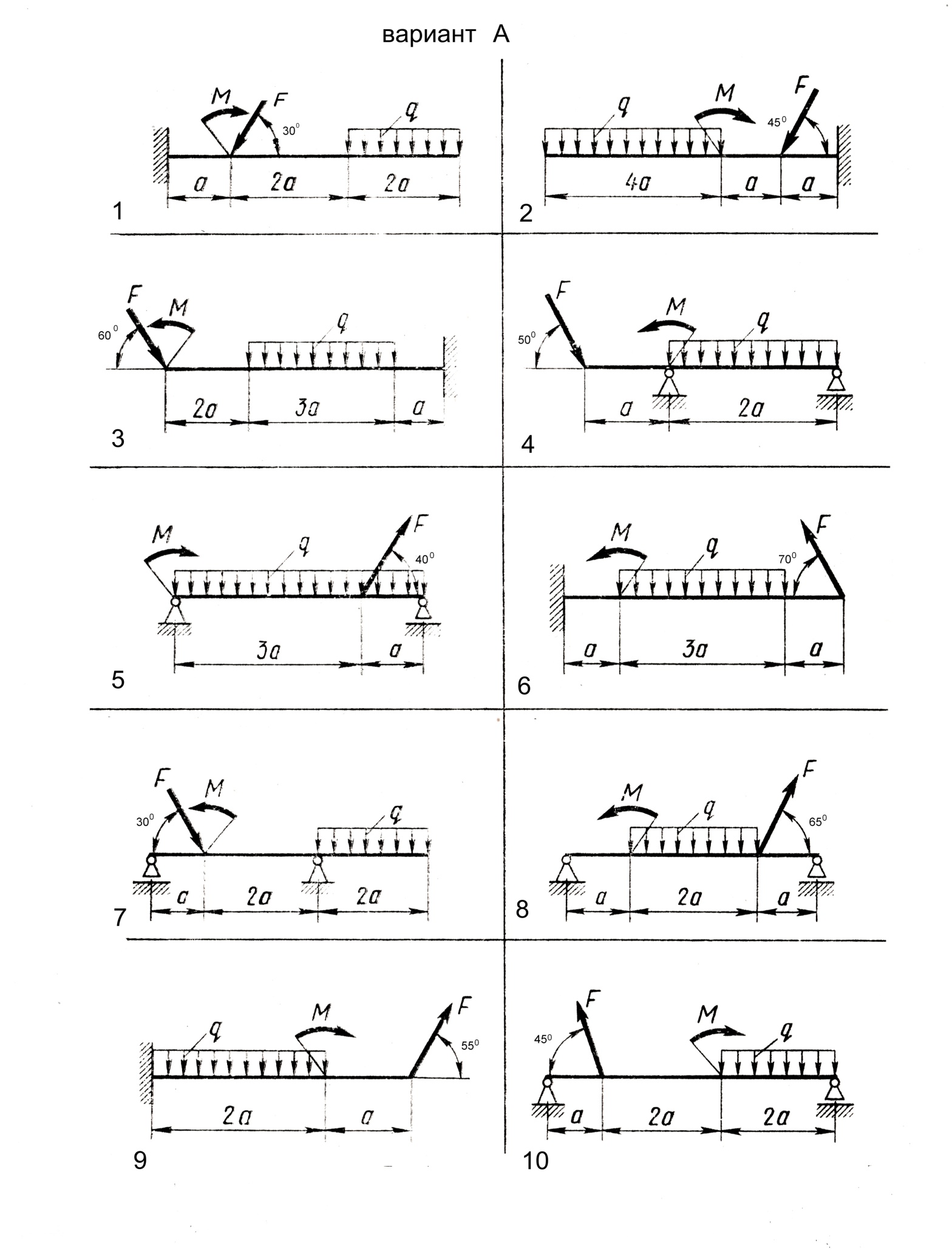
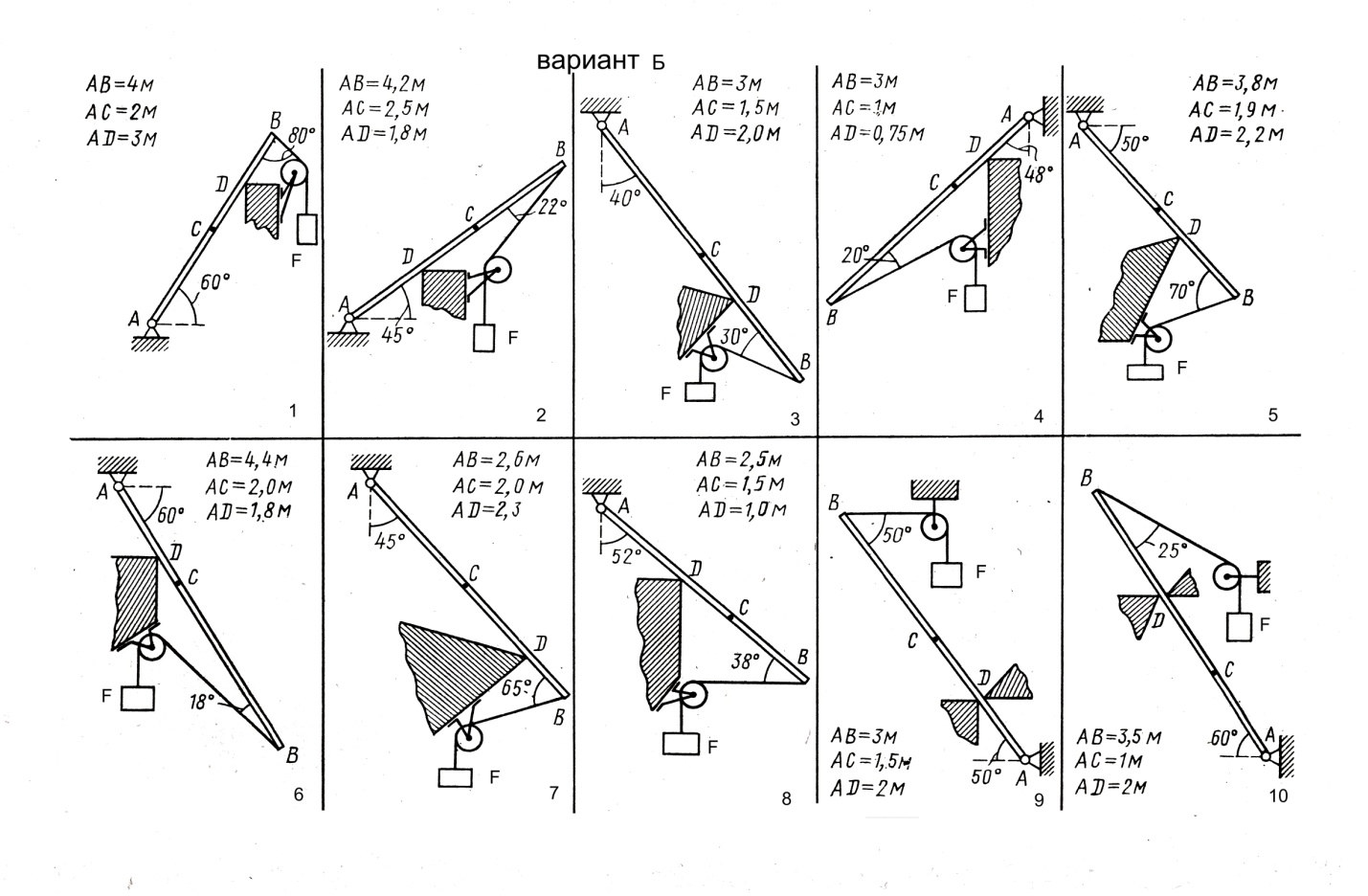
Алгоритм решения
1. Изобразить балку вместе с нагрузками на рисунке, соблюдая при этом заданные размеры ее участков и угла
2. Освободить балку от связей, заменив эти связи их реакциями:
так как направление реакции неподвижного шарнира заранее неизвестно, то эту реакцию следует заменить двумя составляющими, направленными вдоль выбранных осей координат; реакция стержня направлена вдоль его собственной оси;
при свободномопирании тела о связь реакция связи направлена от связи к телу перпендикулярно либо к поверхности тела, либо к поверхности связи. Если брус опирается на выступ стены, значит, реакция выступа направлена перпендикулярно к брусу.
3. К балке приложить заданные силы
4. Приняв точку за начало координат, выбирают координатные оси
5. Составь уравнения равновесия
6. Решая систему уравнений, определить значения искомых реакций
7. Проверяют правильность решения задач с помощью составления неиспользованных до этого уравнений проекций или моментов. Если при подстановке числовых значений заданных и найденных величин образуется тождество вида 0=0, то задача решена правильно.
Пример выполнения
Задача
Определить реакции опор балки, если
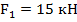 ,
, 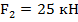 ,
, 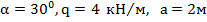 ,
, 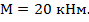
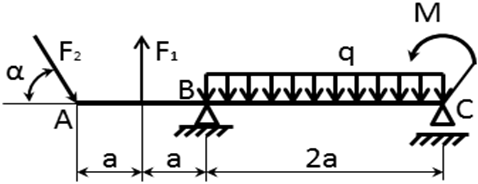
Решение
1. Освободим балку от связей, мысленно отбросив опоры и приложив вместо них неизвестные реакции
Опора В– шарнирно-неподвижная, неизвестна как по модулю, так и по направлению, поэтому изобразим ее в виде составляющих 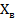
и 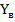 , направленных вдоль выбранных осей координат
, направленных вдоль выбранных осей координат 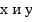 .
.
G AAgAAAAhADj9If/WAAAAlAEAAAsAAAAAAAAAAAAAAAAALwEAAF9yZWxzLy5yZWxzUEsBAi0AFAAG AAgAAAAhAMEThaJ3FQAAKV4BAA4AAAAAAAAAAAAAAAAALgIAAGRycy9lMm9Eb2MueG1sUEsBAi0A FAAGAAgAAAAhANAp2YnhAAAACQEAAA8AAAAAAAAAAAAAAAAA0RcAAGRycy9kb3ducmV2LnhtbFBL BQYAAAAABAAEAPMAAADfGAAAAAA= "> 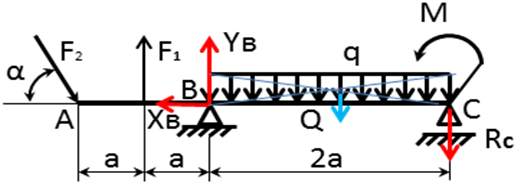
Опора С – шарнирно-подвижная, позволяет перемещаться в области катания катков. В опоре возникает одна реакция, направленная перпендикулярно плоскости, по которой она может перемещаться. В данном случае направим реакцию 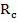 вертикально вверх.
вертикально вверх.
2. Интенсивность – есть равномерно распределенная нагрузка, которая показывает какая величина нагрузки, приходится на единицу длины балки. Если по длине балки интенсивность остается постоянной, то распределенная нагрузка называется равномерной. Ее равнодействующая по модулю равна произведению интенсивности нагрузки на длину участка действия и приложена в ее середине, т.е.
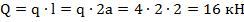
3. Начало осей координат поместим в точку В и для
упрощения уравнений направим оси по неизвестным составляющим
4. Система сил, действующих на балку, представляет плоскую систему произвольно расположенных сил, поэтому для нее можно составить три независимых уравнения равновесия

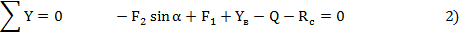
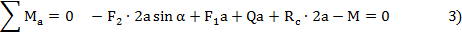
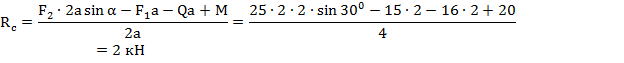
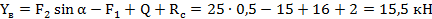
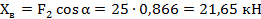
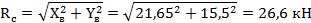
5. Проверка
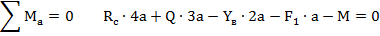
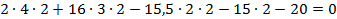
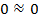
6. Задача решена верно
Задача
Брус АВ, шарнирно закрепленный в точке А, имеет вторую опору в точке D. Сила тяжести G бруса приложена в точке С. К свободному концу Вбруса прикреплена перекинутая через блок нить, несущая груз F=800 Н. Определить реакцию шарнира А и опоры D.
Принять: 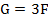

Решение
1. Освобождаем брус от связи. Опоры заменяем реакцией опор.
Опора А – шарнирно - неподвижная, препятствует любому возвратно-поступательному движению, реакция неизвестна ни по модулю, ни по направлению. Разложим ее на две неизвестные составляющие (направим их вдоль осей); имеем
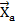 и
и 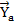
Опора D - балка опирается на ребро, реакция выступа всегда перпендикулярна балке АВ, т.е.
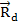
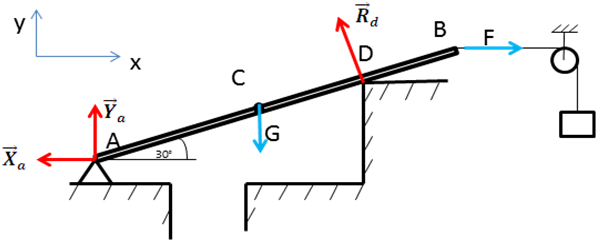
В точке В балка имеет связь в виде гибкой нити, реакция которой всегда направлена вдоль нити в сторону рассматриваемого тела. Реакция нити всегда направлена от тела, т.е.
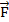
3. Проводим координатные оси
4. Анализируем систему сил. Имеем пять сил, три из которых - неизвестны.
Задача статически определима.
5. Балка находится в равновесии, составляем три уравнения статики
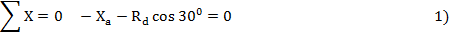
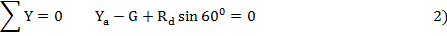
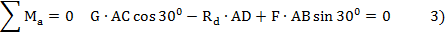
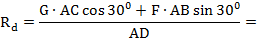
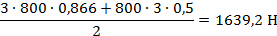
Знак плюс показывает, что направление 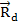 - верно.
- верно.
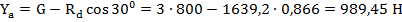
Знак плюс показывает, что направление 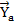 – верно
– верно
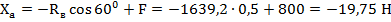
Знак минус показывает, что направление 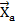 – противоположно выбранному.
– противоположно выбранному.
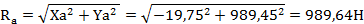
Проверяем правильность решения задачи
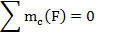
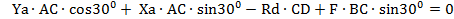
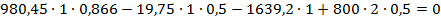
0=0
Задача решена верно
Контрольные вопросы.
1. Что называется связью? Что такое реакция связи?
2. Перечислите виды связей и укажите направление соответствующих им реакций.
3. В каком случае проекция силы на ось равна модулю силы?
4. Что такое момент силы относительно точки? Как назначают знак момента относительно точки?
5. Что называется плечом силы? Как найти плечо силы?
6. Сформулируйте аналитическое условие равновесия плоской системы произвольно расположенных сил.
7. Укажите, как рационально выбрать направление осей координат и центр моментов.
8. Какие нагрузки называются сосредоточенными и распределенными?
9. Что такое интенсивность равномерно распределенной нагрузки? Как найти численное значение, направление и точку приложения равнодействующей равномерно распределенной нагрузки?
10. Укажите три вида уравнений равновесия плоской системы произвольно расположенных сил.
СР №4
