Графическое представление графов
Графы удобно изображать в виде рисунков, состоящих из точек и линий, соединяющих некоторые из этих точек. При этом точки соответствуют вершинам графа, а соединяющие пары точек линии (прямолинейные либо криволинейные) – рёбрам (табл.1).
Таблица 1
| Элементы графов | Геометрические элементы |
| 1. v Î V– вершина | 1. • – точка в пространстве. |
| 2. {u,v} – ребро неориентированного графа | 2. u•−•v – отрезок. |
| 3. (v1,v2) – дуги в ориентированном графе | 3. v1•→v2 – направленный отрезок. |
| 4. {v,v} – петля | 4. 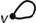 – замкнутый отрезок. – замкнутый отрезок. |
Виды графов
Множество рёбер Е может быть пустым (рис. 1.1). Такой граф называется нуль-графом и обозначается Ø.

рис. 1.1. Нуль-граф
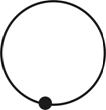
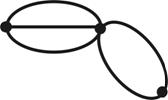
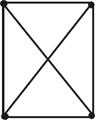
Если же множество вершин V – пустое, то пустым является также множество Е. Такой граф называется пустым. Линии, которые изображают рёбра графа, могут пересекаться, но точки пересечения не являются вершинами (рис. 1.2, а); разные рёбра могут быть инцидентными одной и той же паре вершин (рис. 1.2, б), такие рёбра называются кратными. Этот случай соответствует наличию нескольких одинаковых пар (vi,vj) 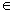 E(G). Граф, который содержит кратные рёбра, называется мультиграфом. Ребро может соединять некоторую вершину саму с собою (рис. 1.2, в), такое ребро называется петлёй. Этот случай соответствует наличию в множестве Е пар вида (v,v). Граф с петлями и кратными рёбрами называется псевдографом. Конечный неориентированный граф без петель и кратных рёбер называется обычным.
E(G). Граф, который содержит кратные рёбра, называется мультиграфом. Ребро может соединять некоторую вершину саму с собою (рис. 1.2, в), такое ребро называется петлёй. Этот случай соответствует наличию в множестве Е пар вида (v,v). Граф с петлями и кратными рёбрами называется псевдографом. Конечный неориентированный граф без петель и кратных рёбер называется обычным.
 | |
 |
 |
а б в
Рисунок 1.2. Графы: а) – обычный, б) – с кратными рёбрами, в) – с петлёй
Элементы графов
Путь – это последовательность рёбер e1, e2, …, em, такая, что рёбра ei, ei+1 имеют общую вершину. Число рёбер называется длинной пути. Если ни одна из вершин не появляется больше одного раза, то путь называется простым. Понятно, что в простом пути ни одно ребро не используется дважды.
Путь называется циклом, если его начальная вершина совпадает с конечной; простым циклом, если это не выполняется для других вершин.
Чередующаяся последовательность v1, e1, v2, e2, …, el,vl+1 вершин и рёбер графа, такая, что ei = vivi+1 (i = 1, l), называется маршрутом. Если v1 = vl+1, то маршрут замкнутый, иначе открытый.
Маршрут называется цепью, если все его рёбра различны, и простой цепью, если все вершины, кроме, возможно, крайних, различны. В цепи 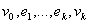 вершины v0 и vk называются концами цепи. Цепь, которая соединяет вершины vi и vj, обозначается
вершины v0 и vk называются концами цепи. Цепь, которая соединяет вершины vi и vj, обозначается 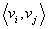
Для орграфов цепь называется путём, а цикл – контуром.
Две вершины в графе называются связными, если существует соединяющая их (простая) цепь. Граф, у которого все вершины связны, называется связным. Ориентированный граф называется сильно связным, если для любых двух вершин существует ориентированный путь, который соединяет их.
