Матричное представление графов

Курсовая работа

Матричное представление графов.

Выполнил студент

Группы ИВТ 42-12

Григорьев Д. А.

Проверил Степанов В. И.

Чебоксары

Оглавление

Введение. 3

Определение графа и основные понятия. 5

Применение графов. 9

Матричное представление графов. 10

Матрица инциденций. 10

Матрица смежности. 11

Матрица разрезов. 12

Цикломатическая матрица. 13

Матрица Кирхгофа. 13

Специальные свойства графов. 14

Решение оптимизационных задач. 15

Алгоритм Дейкстры. 15

Задача коммивояжера. 17

Задача о назначениях. 21

Венгерский алгоритм. 22

Постановка задачи. 22

Матричная интерпретация алгоритма. 22

Реализация на python. 25

Вывод. 28

Список литературы. 29

Введение.

В последние годы особую важность приобрели те разделы математики, которые имеют отношение к развитию цифровых устройств, цифровой связи и цифровых вычислительных машин. Базой для преподавания этих дисциплин наряду с классическими методами анализа непрерывных физических моделей стали алгебраические, логические и комбинаторные методы исследования различных моделей дискретной математики.

Значительно возросла популярность теории графов – ветви дискретной математики. Графы встречаются во многих областях под разными названиями: "структуры" в гражданском строительстве, "сети" – в электронике, "социограммы" – в социологии и экономике, "молекулярные структуры" – в химии, "дорожные карты", электрические или газовые распределительные сети и т. д.

Родившись при решении головоломок и игр, таких, например, как задача о кенигсбергских мостах и игра Гамильтона, теория графов стала мощным средством исследования и решения многих задач, возникающих при изучении больших и сложных систем. Для специалистов по вычислительной технике, информационным системам и системам цифровой связи теория графов – это удобный язык выражения понятий из этой области; многие результаты теории графов имеют непосредственную связь с задачами, с которыми им приходится сталкиваться. Графическая интерпретация различных моделей графов дана на Рис. 1.1 б. Так в виде ориентированных графов можно представить любую логическую или функционально - логическую схему. На таких графовых моделях можно, например, оценить быстродействие схемы. Блок-схема алгоритма может быть представлена вероятностным графом, который позволяет оценить временные характеристики алгоритма, затраты процессорного времени, трудоемкость и другие. Графом типа "дерево" можно отобразить практически любую структуру организации или предприятия.

Широкое применение теория графов получила при исследовании так называемой проблемы оптимизации, возникающей при конструировании больших систем как технических, так и программных, например, таких, как компиляторы.

В рамках этих исследований были разработаны многие, неизвестные ранее теоретико-графовые понятия. Теория графов имеет большую привлекательность для специалистов в области проектирования для построения эффективных алгоритмов и анализа их сложности. Использование аппарата теории графов оказало существенное влияние на разработку алгоритмов конструкторского проектирования схем. Непосредственное и детальное представление практических систем, таких, как распределительные сети, системы связи, приводит к графам большого размера, успешный анализ которых зависит в равной степени, как от эффективных алгоритмов, так и от возможностей компьютерной техники. Поэтому в настоящее время основное внимание сосредоточено на разработке и описании компьютерных алгоритмов анализа графов. В связи с этим основной упор в данном учебном пособии делается на машинные способы представления графов и алгоритмы решения задач на графах, легко реализуемых на ЭВМ.

Определение графа и основные понятия.

Для описания строения различных систем, состоящих из связанных между собой элементов, часто используют графические схемы, изображая элементы точками (кружками, прямоугольниками и т.д.), а связи между ними – линиями или стрелками, соединяющими элементы. При этом получаются диаграммы вроде тех, что показаны на рис. 1.1. На данных диаграммах ни способ изображения элементов, ни форма или длина линий не имеют значения – важно лишь, какие именно пары элементов соединены линиями. Однако, эту же структуру можно представить и без графического изображения, а просто перечислив пары связанных между собой элементов: (1,4), (4,5), (5,3), (3,2), (2,1), (1,3). Таким образом мы получаем два списка: список элементов и список пар элементов. Вместе они составляют то, что математически называют «графом». Граф состоит из двух множеств – множества вершин и множества ребер, причем для каждого ребра указана пара вершин, которые это ребро соединяет.

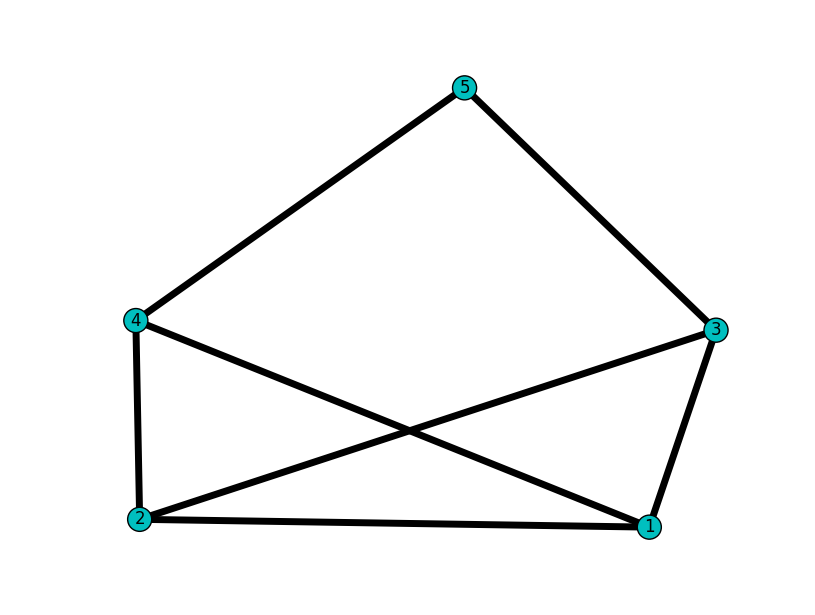Рис 1.1 г

Рис 1.1 а

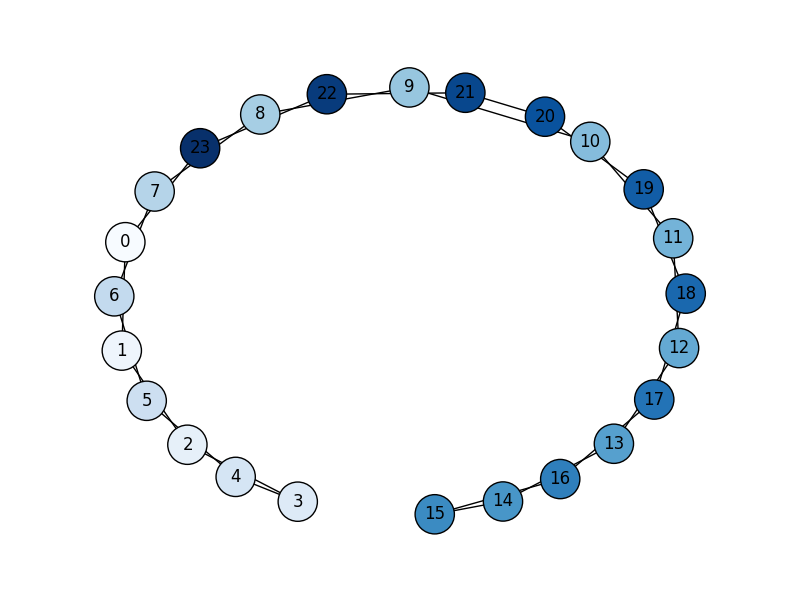
Рис 1.1 в Рис 1.1 б

В листинге 1 приводится пример реализации данного графа (Рис 1.1 в) на языке python с использованием библиотек NetworkX и matplotLib.

Листинг 1.

try:

import matplotlib.pyplot as plt

except:

raise

import networkx as nx

G=nx.cycle_graph(24)

pos=nx.spring_layout(G,iterations=200)

nx.draw(G,pos,node_color=range(24),node_size=800,cmap=plt.cm.Blues)

plt.show() # display

Существует также понятие ориентированный граф или орграф. Это есть граф, ребрам которого присвоено направление. Направленные ребрами именуются также дугами или просто ребрами.

То есть на Рис 1.1 г пара вершин (4, 5) и (5, 4) будет различаться, так как ребро, которое их соединяет, будет иметь направление.

Для ориентированных графов выделяют следующие понятия:

- ребро входит в вершину, если по нему можно двигаться в направлении к этой вершине, и выходит из вершины, если по нему можно двигаться в направлении от этой вершины;
- входящая степень вершины - это число входящих в нее ребер;
- исходящая (или выходящая) степень вершины - это число выходящих из нее ребер;
- путь из вершины A в вершину B - это последовательность ребер и промежуточных вершин, по которым можно дойти из A в B; длина пути определяется, как обычно (число ребер); простой путь - как обычно, путь, в котором вершины (и тем более, ребра) не повторяются;
- ориентированный цикл - это замкнутый простой путь в ориентированном графе;
- сильно связный ориентированный граф - это ориентированный граф, где из любой вершины в любую есть путь (для каждой пары вершин A и B есть как путь из A в B, так и путь из B в A);
- компонента сильной связности - это часть графа, которая сама по себе сильно связна, но ее нельзя расширить так, чтобы она осталась сильно связной; между разными компонентами сильной связности могут быть ребра, но все ребра между двумя разными компонентами направлены в одну и ту же сторону;

- смежные ребра– ребра, которые имеют общую концевую вершину.

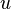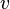Вершины и называются концевыми вершинами (или просто концами) ребра .

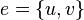По отношению к вершинам ребро eв таком случае называется инцидентным и наоборот.

Ребро, в свою очередь, соединяет эти вершины. Две концевые вершины одного и того же ребра называются соседними.

Однако, существует и такой вариант, при котором две вершины соединяют два ребра. Если в графе существует такое соединение, то говорят, что в графе допускаются кратные ребра. Граф с кратными ребрами называют мультиграфом.

Также, ребро, соединяющее вершину с собой, то есть ребро, которое выходит и входит в одну и ту же вершину называют петлей.

Комбинируя вышеперечисленного можно получить разные варианты определения понятия графа. Чаще всего встречаются графы неориентированные графы без петель и кратных ребер. Такие графы называются обыкновенным графом.

Подграфом графа G называется граф, все вершины и дуги которого содержатся среди вершин и дуг графа G. Всякий подграф может быть получен путем удалением некоторых вершин или ребер.

Сам граф по отношению к своим подграфам называется надграфом (суграфом или суперграфом). На Рис. 1.2 представлен подграф графа, приведенного выше (Рис. 1.1 г).

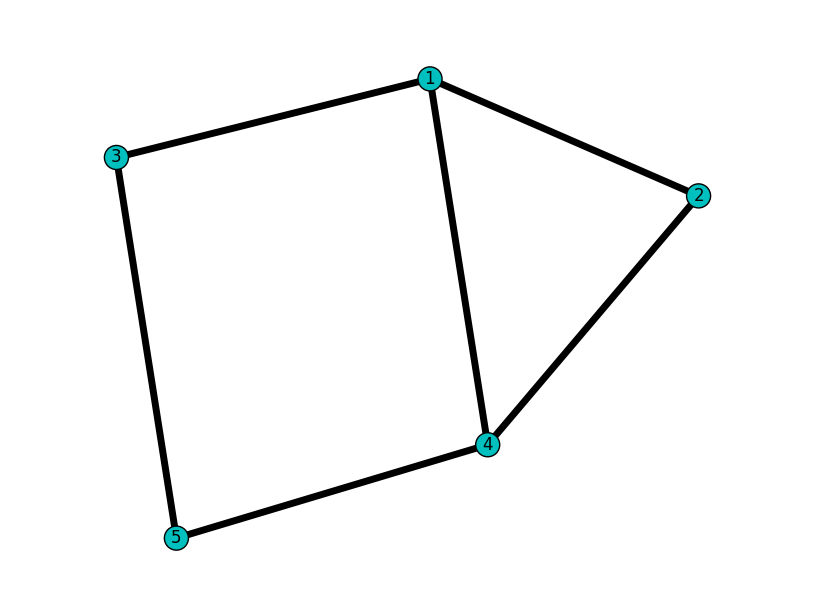
Рис. 1.2

Существует также понятие пустой граф, граф, который не имеет ребер и вершин.

Полным называется граф, в котором две вершины смежны.

Применение графов.

Теория графов находит применение, например, в геоинформационных системах (ГИС). Существующие или вновь проектируемые дома, сооружения, кварталы и т. п. рассматриваются как вершины, а соединяющие их дороги, инженерные сети, линии электропередачи и т. п. — как рёбра. Применение различных вычислений, производимых на таком графе, позволяет, например, найти кратчайший объездной путь или ближайший продуктовый магазин, спланировать оптимальный маршрут.

Теория графов содержит большое количество нерешённых проблем и пока не доказанных гипотез.

Основные сферы применения теории графов:

- В химии (для описания структур, путей сложных реакций, правило фаз также может быть интерпретировано как задача теории графов); компьютерная химия — сравнительно молодая область химии, основанная на применении теории графов. Теория графов представляет собой математическую основу хемоинформатики. Теория графов позволяет точно определить число теоретически возможных изомеров у углеводородов и других органических соединений;

- В информатике и программировании (граф-схема алгоритма);

- В коммуникационных и транспортных системах. В частности, для маршрутизации данных в Интернете;

- В экономике;

- В логистике;

- В схемотехнике (топология межсоединений элементов на печатной плате или микросхеме представляет собой граф или гиперграф).

Выделяют особый вид графа, дерево. Дерево — это связный ациклический граф. Связность означает наличие путей между любой парой вершин, ацикличность — отсутствие циклов и то, что между парами вершин имеется только по одному пути. На Рис 1.3 представлено двоичное дерево.

Двоичное дерево — древовидная структура данных, в которой каждый узел имеет не более двух потомков (детей). Как правило, первый называется родительским узлом, а дети называются левым и правым наследниками.

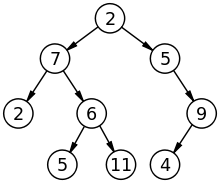
Рис 1.3

Матричное представление графов.

Матрица инциденций.

Развитие алгоритмических подходов к анализу свойств графов требует определенных способов описания графов, более пригодных для практических вычислений, в том числе с использованием ЭВМ. Рассмотрим три наиболее распространенных способа представления графов.

Предположим, что все вершины и все ребра неориентированного графа или все вершины и все дуги (включая петли) ориентированного графа пронумерованы начиная с единицы. Граф (неориентированный или ориентированный) может быть представлен в виде матрицы типа 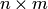, где 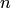— число вершин, а 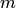— число ребер (или дуг). Для неориентированного графа элементы этой матрицы задаются следующим образом:

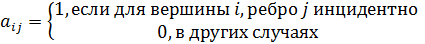
Для ориентированного графа элементы матрицы задаются так:

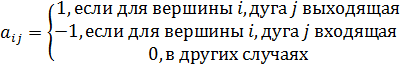
Матрицу 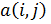типа 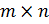, определенную указанным образом, называют матрицей инциденций.

Пример получения матрицы инциденций. Для изображенного ниже графа (Рис. 2.1 а) матрицей инциденций будет матрица, представленная на (Рис 2.1 б).

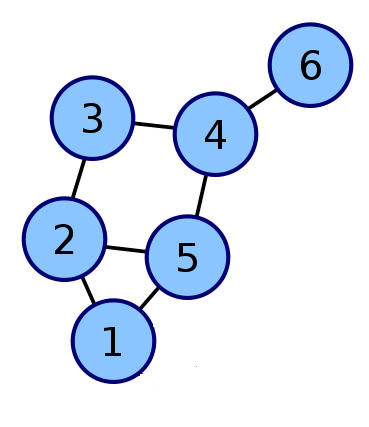
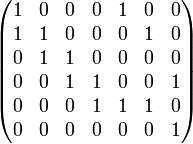
Рис 2.1 а Рис. 2.1 б

Матрица смежности.

Несмотря на то, что представление графа в виде матрицы инциденций играет весьма большую роль в теоретических исследованиях, практически этот способ весьма неэффективен. Прежде всего, в матрице в каждом столбце только два ненулевых элемента, что делает этот способ представления графа неэкономным при большом количестве вершин. Кроме того, решение практических задач с помощью матрицы инциденций весьма трудоемко.

Оценим, например, временные затраты на решение с помощью матрицы инциденций такой простой задачи в ориентированном графе: для данной вершины 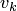найти ее "окружение" — множество преемников и множество предшественников вершины 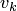, т.е. множество всех вершин, непосредственно достижимых из 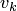, и множество всех вершин, из которых она непосредственно достижима.

Для решения этой задачи на матрице инциденций ориентированного графа нужно идти по строке с номером 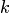до появления ненулевого элемента (+1 или –1). В случае если обнаружена +1, в соответствующем столбце надо найти строку, в которой записано число –1. Номер строки, в которой стоит это число, дает номер вершины, непосредственно достижимой из данной вершины. Если обнаружена –1, в столбце надо найти строку, в которой записана 1, и получить номер вершины, из которой непосредственно достижима данная вершина. Для получения всего "окружения" надо проделать указанный поиск для всех ненулевых элементов k-й строки. Наиболее трудоемкой процедурой является поиск ненулевого элемента в столбце. Число таких процедур поиска равно степени вершины 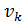. Будем в этом случае говорить, что сложность алгоритма анализа окружения вершины 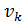составляет 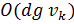(порядка ).

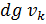Можно увидеть, что поиск "окружения" всех вершин займет время порядка произведения числа вершин ориентированного графа на сумму степеней всех вершин, которая, как можно показать, пропорциональна числу дуг ориентированного графа. Таким образом, сложность алгоритма поиска "окружения" составляет 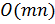, т.е. поиск занимает время порядка произведения числа вершин на число дуг.

Более эффективной матричной структурой, представляющей граф, служит матрица смежности вершин, или булева матрица графа. Это квадратная матрица В порядка n, элементы которой определяют следующим образом:

для неориентированного графа: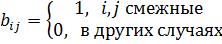

для ориентированного графа:

Для изображенного ниже графа (Рис. 2.2 а) матрицей инциденций будет матрица, представленная на (Рис 2.2 б).

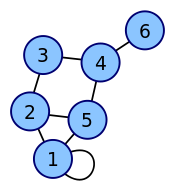Рис 2.2 а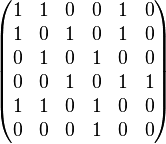

Рис 2.2 б

Матрица разрезов.

Рассмотрим орграф 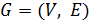. Если 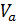– непустое подмножество множества 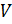, то множество дуг, соединяющих вершины 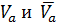, является разрезом, обозначаемым 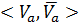. Ориентацию 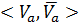можно принять как от вершины 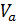к вершине 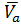, так и наоборот. Допустим, мы принимаем ориентацию от вершины 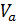к вершине 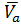. Тогда говорят, что ориентация дуги из 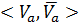соответствует ориентации разреза 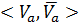, если дуга ориентирована от вершины из 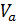в вершину из .

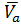Матрица разрезов 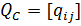графа 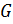с m ребрами имеет m столбцов и столько строк, сколько в этом графе имеется разрезов. Элемент 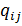определяется следующим образом.

Если граф ориентированный,

Если граф неориентированный,

Строки матрицы 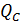называются векторами разрезов.