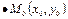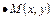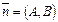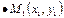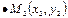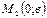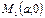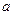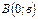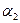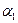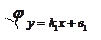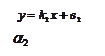Уравнения прямой на плоскости
Тема 4. Аналитическая геометрия на плоскости
Пусть на плоскости задана система координат. Рассмотрим уравнение вида
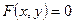 . (4.1)
. (4.1)
Это равенство, если оно выполняется не для всех пар чисел 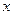 и
и 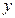 , называется уравнением некоторой линии
, называется уравнением некоторой линии 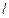 в заданной системе координат
в заданной системе координат  . Уравнение (4.1) определяет или задает линию
. Уравнение (4.1) определяет или задает линию 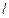 .
.
Известно, что любое линейное уравнение с двумя переменными определяет прямую линию на плоскости.
Чтобы написать уравнение прямой 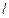 , ее надо задать. Существуют разные способы задания прямой, что приводит к различным по форме уравнениям, которые равносильны между собой, так как имеют одно и то же множество решений – координаты точек прямой
, ее надо задать. Существуют разные способы задания прямой, что приводит к различным по форме уравнениям, которые равносильны между собой, так как имеют одно и то же множество решений – координаты точек прямой 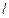 .
.
Зададим прямую 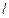 при помощи точки
при помощи точки 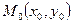 , принадлежащей данной прямой, и ненулевого вектора
, принадлежащей данной прямой, и ненулевого вектора 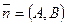 , перпендикулярного этой прямой (рис. 4.1).
, перпендикулярного этой прямой (рис. 4.1).
О Рис. 4.1 | Эти условия однозначно определяют прямую, так как через точку перпендикулярно вектору можно провести только одну прямую. Пусть 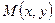 - произвольная точка прямой - произвольная точка прямой 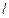 . Так как . Так как 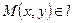 , то , то 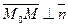 и и 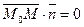 , т.е. , т.е. |
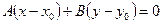 . (4.2)
. (4.2)
Каждый ненулевой вектор 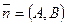 , перпендикулярный данной прямой, называется ее нормальным вектором.
, перпендикулярный данной прямой, называется ее нормальным вектором.
Уравнение (1.2) называется уравнением прямой, заданной с помощью нормального вектора и точки.
Зададим прямую 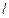 при помощи двух точек
при помощи двух точек 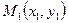 и
и 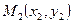 , принадлежащих этой прямой.
, принадлежащих этой прямой.
Эти условия однозначно определяют прямую, так как через две заданные точки можно провести только одну прямую.
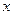 Рис. 4.2. | Пусть 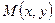 - произвольная точка прямой - произвольная точка прямой 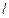 . Так как . Так как 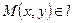 , то , то 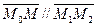 и и 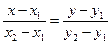 (4.3) (4.3) |
Уравнение (4.3) называется уравнением прямой, проходящей через две заданные точки.
Уравнения (4.2) и (4.3) с помощью тождественных преобразований приводятся к равносильному виду
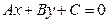 . (4.4)
. (4.4)
Уравнение (4.4) называется общим уравнением прямой линии. Здесь  - какие-либо числа. Некоторые коэффициенты могут равняться нулю, однако хотя бы одно из чисел
- какие-либо числа. Некоторые коэффициенты могут равняться нулю, однако хотя бы одно из чисел 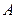 или
или 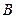 должно быть отлично от нуля, иначе в уравнении исчезнут обе текущие координаты
должно быть отлично от нуля, иначе в уравнении исчезнут обе текущие координаты 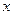 и
и 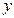 .
.
Если в (4.4) какой-либо из коэффициентов равен нулю, то:
1) при 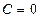 :
: 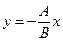 - прямая проходит через начало координат;
- прямая проходит через начало координат;
2) при 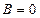 (
( 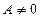 ):
): 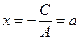 - прямая, параллельная оси
- прямая, параллельная оси 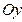 ;
;
3) при 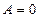 (
( 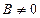 ):
): 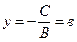 - прямая, параллельная оси
- прямая, параллельная оси 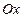 ;
;
4) при 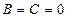 :
: 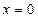 - ось
- ось 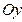 ;
;
5) при 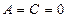 :
: 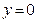 - ось
- ось 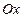 .
.
О Рис. 4.3 | Если ни один из коэффициентов уравнения (4.4) не равен нулю, то его можно преобразовать к виду: 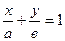 , (4.5) где , (4.5) где 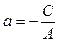 и и 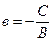 - величины направленных отрезков, которые отсекает прямая на осях координат (рис. 4.3). - величины направленных отрезков, которые отсекает прямая на осях координат (рис. 4.3). |
Уравнение (4.5) называется уравнением прямой «в отрезках».
Из уравнения (4.4) можно выразить переменную 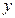 как функцию от аргумента
как функцию от аргумента 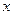 при
при 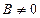 :
:
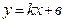 . (4.6)
. (4.6)
Уравнение (4.6) известно из элементарной математики, его называют уравнением с угловым коэффициентом.
Угловой коэффициент 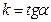 , где
, где 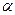 - меньший из неотрицательных углов, образуемых прямой
- меньший из неотрицательных углов, образуемых прямой 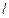 с положительным направлением оси
с положительным направлением оси 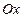
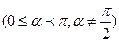 . Ордината точки пересечения прямой с осью
. Ордината точки пересечения прямой с осью 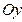 равна
равна 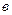 (рис. 4.4).
(рис. 4.4).
Приведем еще некоторые сведения справочного характера.
Если известны угловые коэффициенты 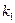 и
и 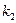 двух прямых (рис. 4.5.), то один из углов
двух прямых (рис. 4.5.), то один из углов 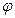 между этими прямыми определяется по формуле
между этими прямыми определяется по формуле
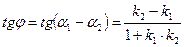 . (4.7)
. (4.7)
Второй угол равен 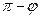 .
.
   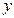
О Рис. 4.4 |     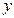
О Рис. 4.5 |
Условие параллельности двух прямых:
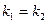 . (4.8)
. (4.8)
Условие перпендикулярности двух прямых:
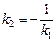 . (4.9)
. (4.9)
Точка пересечения прямых 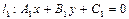 и
и 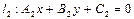 определяется как решение системы:
определяется как решение системы:
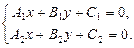 (4.10)
(4.10)
Расстоянием 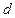 от точки
от точки 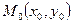 до прямой
до прямой 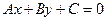 называется длина перпендикуляра, опущенного из этой точки на прямую. Расстояние
называется длина перпендикуляра, опущенного из этой точки на прямую. Расстояние 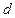 определяется по формуле
определяется по формуле
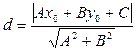 . (4.11)
. (4.11)