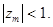Анализ устойчивости во временной области

Лекция 10. Анализ ЦС во временной и частотной области

Общие признаки устойчивости остаются справедливыми и для импульсных систем, однако наличие импульсных элементов вызывает дополнительные сложности при анализе устойчивости.

Анализ устойчивости во временной области

Как и в непрерывных системах, общее решение разностного уравнения импульсной системы можно представить в виде частного решения уравнения с правой частью и общего решения без правой части.

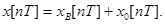(10.1)

Составляющая x_B[nT] описывает вынужденное движение системы, а x₀[nT] – переходное движение. Об устойчивости движения системы можно судить по составляющей x[nT], определяемой из решения однородного уравнения.

Проектирование непрерывных систем часто основывается на анализе расположения нулей и полюсов ПФ системы на Р-плоскости. Если при этом все полюсы ПФ замкнутой системы, т.е. корни характеристического уравнения лежат в левой полуплоскости корней Р, то система устойчива. Границей устойчивости является мнимая ось (рисунок 10.1).

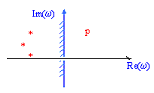
Рисунок 10.1 – Корни на плоскости Р для устойчивой системы

Уравнение для замкнутой импульсной системы в z-изображении позволяет получить характеристическое уравнение и, если его корни z₁, z₂ …z_n, например, действительны, то решение характеристического уравнения можно записать в виде

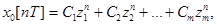(10.2)

где С₁, С₂ …С_m – постоянные коэффициенты, определяемые из начальных условий.

Система будет устойчива, если при t→∞ или n→∞ сигнал х стремится к нулю, т.е.

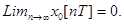(10.3)

В свою очередь, это условие выполнимо, если все корни z₁, z₂, ..z_m по модулю не превосходят единицы.

Следовательно, необходимым и достаточным условием устойчивости импульсной системы является соблюдение неравенства

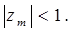(10.4)

Подставляя p=jω в z = e^pT, получим z = ej^ωT. При изменении ω от 0 до 2π/Т переменная z описывает в Z-плоскости окружность единичного радиуса. При дальнейшем увеличении ω от 2π/Т до 4π/Т переменная повторно описывает окружность. Следовательно, отрезок мнимой оси в Р-плоскости, являющимся границей устойчивости, отражается в единичную окружность в Z-плоскости с центром в начале координат (рисунок 10.2).

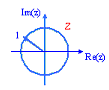
Рисунок 10.2 – Отображение границы устойчивости на Z-плоскости

Левой Р-полуплоскости соответствует на плоскости корней Z внутренняя поверхность круга единичного радиуса. Точки же правой половины Р-плоскости отображаются в область вне единичного круга на z-плоскости.

Определение устойчивости линейной импульсной системы по расположению корней является сложной задачей при высоком порядке характеристического уравнения. Критерии устойчивости освобождают вычисление корней и устанавливают соотношения для определения устойчивости, вытекающие из основного неравенства корней