Уравнение прямой, проходящей через данную точку с задан. нормальным вектором

	Пусть прямая l проходит через точку М0 с координатами (х0, y0), и перпендикулярна вектору n(A,B). Вектор, перпендикулярный данной прямой, называется нормальным вектором этой прямой. Возьмем на прямой произвольную точку М(х,y). Векторы M0M и n перпендикулярны, а значит, их скалярное произведение равно 0, т.к. М0М имеет координаты (х-х0, y-y0):

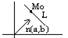
n ∙ M₀M=0.

Запишем это равенство в координатной форме: А(х-х₀) – В(у-у₀)=0. Это и есть уравнениепрямой, проходящей через задан.точку с задан. нормальн.вектором.

Каноническое и параметрическое уравнение прямой.

Канонич. уравнение: Пусть прямая L проходит через точку М₀(х₀,у₀) и параллельно вектору N(а₁,а₂). Вектор, параллельный данной прямой, называется направляющим вектором этой прямой. Возьмем на прямой L произвольную точку М(х,у). Тогда векторы M₀M и n коллинераны, а значит их соответствующие координаты пропорциональны. Т.к. M₀M (x-x₀, y-y₀), то получим:

х-х₀ = у-у₀

а₁ а₂ - каноническое уравнение прямой, или уравнение прямой, проход. через данную точку с заданным направляющим вектором.

Параметрич.уравнение: Из канонич. уравнения прямой, т.к. левая часть равна правой, можно записать, что:

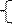
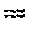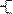или 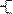- параметрическое уравнение прямой.

Угол между прямыми.

Пусть требуется определить угол между прямыми l₁ и l₂, заданными в плоскости Oxy уравнениями А₁х+В₁у+С₁=0 и А₂х+В₂у+С₂=0. Очевидно, что n₁=(A₁;B₁) является нормальным вектором прямой l₁, а n₂=(A₂;B₂) – нормальный вектор прямой l₂. Кроме того, угол φ между нормальными векторами n₁ и n₂ равен одному их углов, образованных прямыми l₁ и l_2.

φ=(n₁^n₂) = (l₁^l₂).

Но : ___n_{1 ∙} n_{2_____}

cos φ=│n₁│∙│n₂│

Записав правую часть последнего равенства в координатной форме, получаем:

__A₁A₂ + B₁B_{2____}

cos φ = √A²₁+B²₁ √ A²₂+B²₂

Эта формула служит для определения угла между двумя прямыми, заданными их общими уравнениями.

Условие параллельности прямых.

Если прямые l₁ и l₂ параллельны между собой, то их нормальные векторы n₁=(A₁;B₁) и n₂=(A₂;B₂) коллинеарны. Считая, что ни одна из прямых не колллинеарна осям координат, запишем условие коллинеарности векторов n₁ и n₂ в координатной форме:

А₁/A₂=B₁/B₂=C₁/C₂ ó k₁=k₂.

К этому же выводу можно прийти и из геометрических соображений. Если l₁ ║ l₂, то α₁= α₂.

Условие перпендикулярности прямых.

Если прямые l₁ и l₂ взаимно перпендикулярны, то взаимно перпендикулярны и их нормальные вектора n₁=(A₁;B₁) и n₂=(A₂;B₂). Запишем условие перпендикулярности векторов n₁ и n₂ в координатной форме:

А₁А₂ + В₁В₂=0.

Считая, В₁≠0 и В₂≠0, имеем: _ __1__

А₁/В₁ ∙ А₂/В₂ +1= 0 ó k₁ ∙ k₂=0, или k₁= k₂ , если k₂≠0.

Таким образом, прямые взаимно перпендикулярны тогда и только тогда, когда их угловые коэффициенты обратны по величине и противоположны по знаку. (Например, 2/3 и -3/2).