Определители второго и третьего порядка. Обратная матрица
Определителем второго порядка, соответствующим матрице
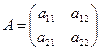 называется число
называется число 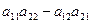 .
.
Этот определитель обозначают 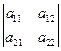 или
или 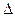 .
.
Следовательно, согласно определению 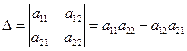 .
.
Определителем третьего порядка, соответствующим матрице 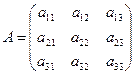 , называется число, обозначаемое
, называется число, обозначаемое 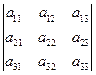 или
или 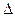 и определяемое равенством
и определяемое равенством
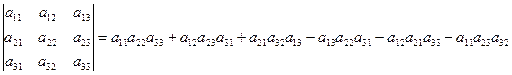 .
.
Для запоминания этого определения существует простое правило, которое называется «правилом треугольников». Каждое слагаемое, стоящее в правой части со знаком плюс, представляет собой произведение трех элементов определителя, взятых, как показано на схеме 1. Каждое слагаемое, стоящее со знаком минус, представляет собой произведение трех элементов определителя, взятых, как показано на схеме 2.
Схема 1 Схема 2














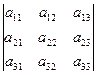
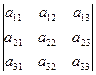
Минором элемента 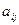 (i =1,2,3; j =1,2.3) определителя третьего порядка называется определитель второго порядка, получающийся из данного определителя третьего порядка вычеркиванием i-той строки j-того столбца, на пересечении которых стоит элемент
(i =1,2,3; j =1,2.3) определителя третьего порядка называется определитель второго порядка, получающийся из данного определителя третьего порядка вычеркиванием i-той строки j-того столбца, на пересечении которых стоит элемент 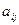 . Минор элемента
. Минор элемента 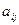 обозначают
обозначают 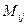 .
.
Алгебраическим дополнением элемента 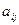 определителя третьего порядка называется произведение минора
определителя третьего порядка называется произведение минора 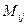 этого элемента на число
этого элемента на число 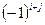 , где i - номер строки, j - номер столбца, на пересечении которых стоит элемент
, где i - номер строки, j - номер столбца, на пересечении которых стоит элемент 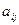 . Алгебраическое дополнение элемента
. Алгебраическое дополнение элемента 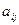 обозначают
обозначают 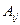 .
.
Таким образом,
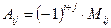
Справедлива следующая теорема.
Определитель равен сумме произведений элементов какой-нибудь строки (или столбца) на их алгебраические дополнения, т.е.
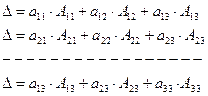
Матрица 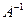 называется обратной матрицей по отношению к матрице
называется обратной матрицей по отношению к матрице 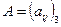 , если выполняется условие:
, если выполняется условие: 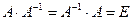 , где
, где 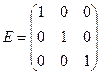 - единичная матрица.
- единичная матрица.
Если определитель матрицы А отличен от нуля, то существует единственная обратная матрица 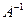 , которая находится по формуле:
, которая находится по формуле:
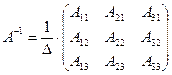 ,
,
где ∆ - определитель матрицы А, 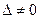 ,
, 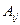 - алгебраические дополнения элементов матрицы А.
- алгебраические дополнения элементов матрицы А.
Задание 2. Найти матрицу, обратную к данной матрице А.
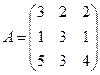 .
.
Решение.
1) Вычислим определитель матрицы А:
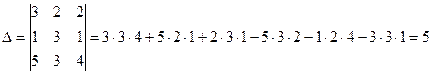 .
.
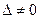 , следовательно, обратная матрица существует и единственна.
, следовательно, обратная матрица существует и единственна.
2) Находим алгебраические дополнения элементов определителя
матрицы А.
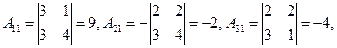
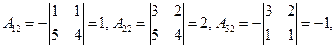
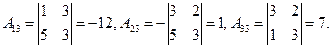
3)  Составим обратную матрицу:
Составим обратную матрицу:
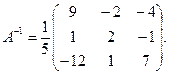
4) Проверим правильность нахождения матрицы 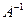 , исходя из
, исходя из
определения обратной матрицы.
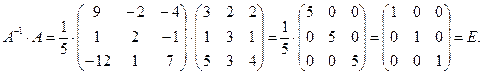
Аналогично 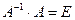 . Следовательно, обратная матрица найдена верно.
. Следовательно, обратная матрица найдена верно.
Системы линейных алгебраических уравнений
Рассмотрим систему трех линейных алгебраических уравнений с тремя неизвестными:
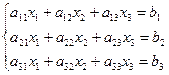 (1)
(1)
Здесь 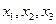 - неизвестные,
- неизвестные, 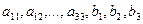 - заданные числа. Определитель
- заданные числа. Определитель 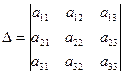 называют определителем системы (1).
называют определителем системы (1).
Система называется совместной, если она имеет хотя бы одно
решение.
Формулы Крамера
Если определитель системы (1) отличен от нуля, то система (1) совместна и имеет единственное решение, которое находится по формулам:
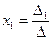 ,
, 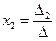 ,
, 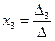 ,
,
где
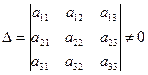 ,
,
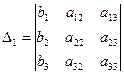 ,
, 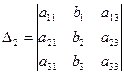 ,
, 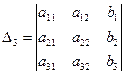
(формулы Крамера).
