Производная функции и ее приложения
Производная функции, ее геометрический и механический смыслы. Дифференцируемость функции. Дифференциал функции и его геометрический смысл. Связь дифференциала с производной. Правила вычисления производных: производная суммы, произведения, частного, производная обратной функции, производная параметрически заданной функции. Таблица производных. Производные и дифференциалы высших порядков.
Теоремы Ролля, Лагранжа, Коши. Правило Лопиталя. Формула Тейлора с остаточным членом в форме Лагранжа. Условия монотонности функции. Точки экстремума. Необходимое условие экстремума, достаточные условия экстремума функции. Исследование функции с помощью производной второго порядка. Точка перегиба. Асимптоты графика функции. Общая схема исследования и построения графика функции.
Неопределенный и определенный интегралы
Первообразная. Неопределенный интеграл и его свойства. Таблица основных формул интегрирования. Непосредственное интегрирование. Интегрирование по частям и подстановкой. Интегрирование рациональных функций. Интегрирование выражений, содержащих тригонометрические функции. Интегрирование некоторых иррациональных функций.
Определение и геометрический смысл определенного интеграла. Основные свойства определенного интеграла. Производная интеграла по верхнему пределу. Формула Ньютона-Лейбница. Замена переменной в определенном интеграле. Интегрирование по частям. Геометрические приложения определенного интеграла: вычисление площади плоской фигуры, площади криволинейного сектора, объем тела вращения и длины дуги плоской кривой. Несобственные интегралы.
Контрольная работа №1
Элементы векторной алгебры и аналитической геометрии.
Комплексные числа
1 – 10. Даны векторы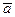 
, 
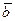и 
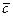. Найдите :
а) скалярное произведение векторов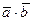 
;
б) векторное произведение векторов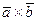 
;
в) смешанное произведение векторов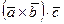 
;
г) проекцию вектора 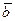на вектор ;
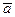д) площадь треугольника, построенного на векторах , ;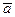
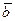е) объем пирамиды, построенной на векторах , , .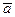
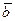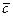1. 
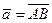, А(1; 2; 21), В(21; 0; 1), 
, 
.
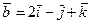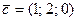2. 
, 
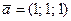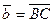, В(0; 1; 2), С(2; 21; 0), 
.
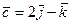3. 
, 
, 
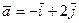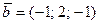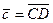, С(0; 2; 21), D(21; 22; 21).
4. 
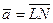, L(1; 2; 3), N(21; 2; 0), 
, 
.
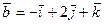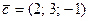5. 
, 
, 
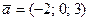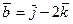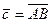, A(0; 22; 1), B(1; 2; 21).
6. 
, 
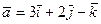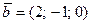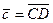, , C(0; 2; 3), D(2; 21; 21).
7. 
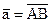, A(2; 22; 2), B(1; 0; 21), 
, 
.
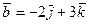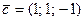8. 
, 
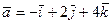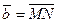, M(3; 1; 22), N(0; 21; 22), 
.
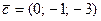9. 
, 
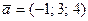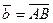, A(22; 1; 3), B(1; 0; 23), 
.
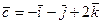10. 
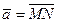, M(22; 3; 4), N(0; 22; 3), 
, 
.
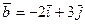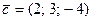11 – 20.Заданы координаты вершин пирамиды ABCD.
1. Составьте:
а) уравнение плоскости, проходящей через точки А, В, С;
б) уравнение прямой, проходящей через точки А, В;
в) уравнение прямой, проходящей через точку D, перпендикулярно плоскости (АВС).
2. Найдите:
а) длину ребра АВ;
б) угол между ребрами АВ и АD;
в) угол между ребром AD и гранью ABC.
11. A(3; 5; 4), B(8; 7; 4), C(5; 10; 4), D(4; 7; 8).
12. A(2; 0; 0), B(1; 0; 1), C(0; 21; 0), D(1; 21; 1).
13. A(7; 7; 3), B(6; 5; 8), C(3; 5; 8), D(8; 4; 1).
14. A(0; 1; 0), B(1; 0; 0), C(21; 21; 1), D(2; 2; 1).
15. A(10; 6; 6), B(22; 8; 2), C(6; 8; 9), D(7; 10; 3).
16. A(4; 2; 5), B(0; 7; 2), C(0; 2; 7), D(1; 5; 0).
17. A(4; 4; 10), B(4; 10; 2), C(2; 8; 4), D(9; 6; 4).
18. A(1; 1; 0), B(0; 1; 2), C(1; 0; 21), D(21; 2; 1).
19. A(21; 2; 21), B(1; 1; 2), C(0; 2; 1), D(2; 21; 22).
20. A(1; 8; 2), B(5; 2; 6), C(5; 7; 4), D(4; 10; 9).
21 – 30. Задачи по аналитической геометрии на плоскости.
21. Точка С(21; 3) – вершина прямого угла равнобедренного прямоугольного треугольника, гипотенуза которого задана уравнением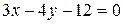 
. Найдите уравнения катетов этого треугольника.
22. Заданы уравнение стороны прямоугольника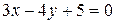 
и две его вершины А(1; 23) и С(1; 2). Найдите уравнения остальных сторон прямоугольника.
23. Заданы А(1; 3) 2 вершина треугольника АВС и уравнения двух медиан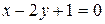 
и 
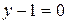. Найдите уравнения сторон треугольника.
24. Составьте уравнения прямых, проходящих через точку М(2; 23) и образующих угол 45° с прямой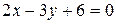 
.
25. Точки А(23; 22), В(4; 21), С(1; 3) – вершины трапеции ABCD (AD||BC). Диагонали трапеции взаимно перпендикулярны. Найдите координаты вершины D этой трапеции.
26. Точки А(3; 4), В(21; 2), С(2; 21) – вершины треугольника. Найдите уравнение медианы, проведенной из вершины А, и уравнение средней линии, параллельной стороне ВС.
27. Заданы уравнения двух сторон параллелограмма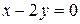 
, 
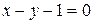и точка пересечения диагоналей А(3; 21). Найдите уравнения двух других сторон.
28. Найдите координаты центра и радиус окружности, проходящей через точки А(1; 5), B(24; 0), C(4; 24).
29. В треугольнике АВС заданы уравнения стороны АВ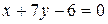 
и биссектрис AD 
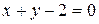и ВЕ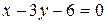 
. Найдите координаты вершин.
30. Найдите координаты точки А, симметричной точке В(23; 1) относительно прямой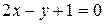 
.
31 – 40. Постройте кривые второго порядка:
31. а)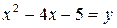 
,
32. а)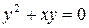 
,
33. а)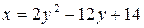 
,
34. а)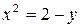 
,
35. а)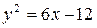 
,
36. а)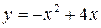 
,
б)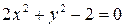 
.
б)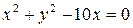 
.
б)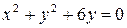 
.
б)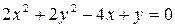 
.
б)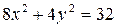 
.
б)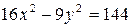 
.
37. а)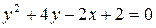 
,
38. а)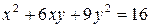 
,
39. а)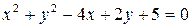 
,
40. а)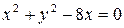 
,
б)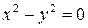 
.
б)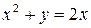 
.
б)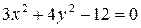 
.
б)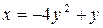 
.
41 – 50. Постройте линию по уравнению в полярных координатах, задавая угол φ от 0 до 2π с шагом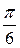 
. Запишите уравнение кривой в декартовой прямоугольной системе координат и определите вид кривой.
41. 
.
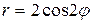43. 
.
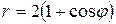45. 
.
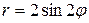47. 
.
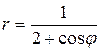49. 
.
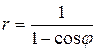42. 
.
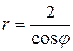44. 
.
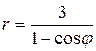46. 
.
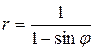48. 
.
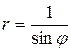50. 
.
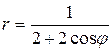51 – 60. Задано комплексное число z.
a) Запишите число z в алгебраической, тригонометрической и показательной формах.
б) Найдите все корни уравнения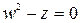 
.
51. 
.
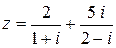53. 
.
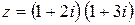55. 
.
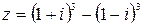57. 
.
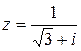59. 
.
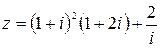52. 
.
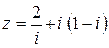54. 
.
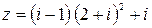56. 
.
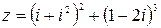58. 
.
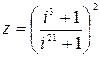60. 
.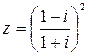