Простейшие задачи в декартовых координатах
Рассмотрим задачу нахождения проекции направленного отрезка на ось. Пусть в пространстве задан направленный отрезок 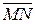 . Предположим, что на оси
. Предположим, что на оси 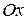 введены декартовы координаты. Проекцией направленного отрезка
введены декартовы координаты. Проекцией направленного отрезка 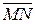 на ось
на ось 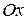 называется величина направленного отрезка
называется величина направленного отрезка 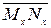 , началом которого служит проекция точки
, началом которого служит проекция точки  на ось
на ось 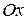 , а концом – проекция точки
, а концом – проекция точки  на эту ось. Указанная проекция обозначается:
на эту ось. Указанная проекция обозначается: 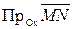 . Для нахождения этой проекции перенесем направленный отрезок
. Для нахождения этой проекции перенесем направленный отрезок 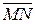 параллельно самому себе так, чтобы его начало попало на ось
параллельно самому себе так, чтобы его начало попало на ось 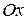 . Обозначим через
. Обозначим через 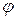 наименьший угол между полученным направленным отрезком и осью
наименьший угол между полученным направленным отрезком и осью 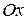 . Если
. Если 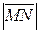 - длина рассматриваемого отрезка, то получаем:
- длина рассматриваемого отрезка, то получаем:
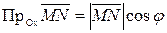 .
.
Рассмотрим теперь задачу нахождения расстояния между двумя точками по известным координатам этих точек. Эта задача уже решена нами на оси. Пусть в пространстве  заданы точки
заданы точки 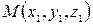 и
и 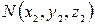 . Очевидно, что расстояние между этими точками равно длине диагонали параллелепипеда, грани которого параллельны координатным плоскостям и проходят через точки
. Очевидно, что расстояние между этими точками равно длине диагонали параллелепипеда, грани которого параллельны координатным плоскостям и проходят через точки  и
и 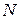 . Длина параллельного оси
. Длина параллельного оси 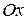 ребра этого параллелепипеда равна, очевидно, абсолютной величине проекции направленного отрезка
ребра этого параллелепипеда равна, очевидно, абсолютной величине проекции направленного отрезка 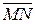 на ось
на ось 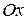 , т.е., согласно следствию теоремы пункта 1, равна
, т.е., согласно следствию теоремы пункта 1, равна 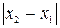 . По аналогичным соображениям длины ребер, параллельных осям
. По аналогичным соображениям длины ребер, параллельных осям 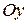 и
и 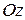 , равны соответственно
, равны соответственно 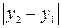 и
и 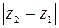 . Используя теорему Пифагора, получим следующую формулу:
. Используя теорему Пифагора, получим следующую формулу:
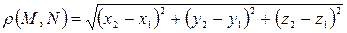 .
.
 Заметим, что на плоскости расстояние между точками
Заметим, что на плоскости расстояние между точками 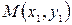 и
и 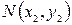 определяется равенством:
определяется равенством:
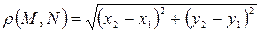 .
.
Рассмотрим задачу, связанную с делением отрезка в заданном отношении. Пусть на отрезке 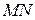 задана точка
задана точка 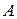 , отличная от границ этого отрезка. Говорят, что точка
, отличная от границ этого отрезка. Говорят, что точка 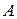 делит отрезок
делит отрезок 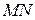 в отношении
в отношении 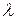 , если
, если
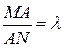 .
.
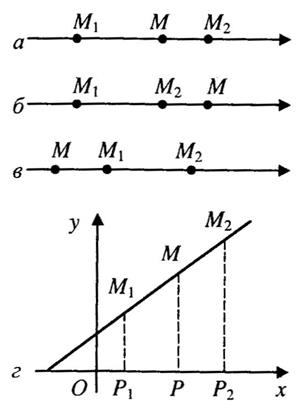
Пусть на плоскости 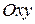 заданы точки
заданы точки 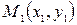 и
и 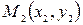 . Найдем координаты точки
. Найдем координаты точки 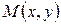 , про которую известно, что она делит отрезок
, про которую известно, что она делит отрезок 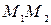 в отношении
в отношении 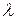 . Спроектируем точки
. Спроектируем точки 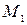 ,
, 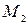 и
и  на ось абсцисс. Получим соответственно точки
на ось абсцисс. Получим соответственно точки 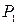 ,
, 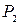 и
и 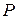 . Из подобия треугольников (см. рис.) очевидно, что
. Из подобия треугольников (см. рис.) очевидно, что
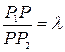 .
.
С другой стороны нам известно, что
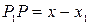 ,
,
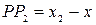 .
.
Отсюда следует равенство
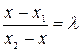
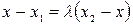
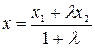 .
.
Аналогично спроектировав рассматриваемые точки на оси  , получим формулы для нахождения ординаты точки
, получим формулы для нахождения ординаты точки 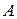 :
:
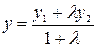 .
.
Отметим частный случай, когда 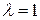 . В этом случае точка
. В этом случае точка 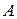 делит отрезок
делит отрезок 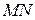 пополам, и мы получаем следующие равенства:
пополам, и мы получаем следующие равенства:
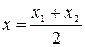 ,
,
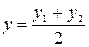 .
.
Заметим, что аналогичные формулы будут справедливы и при делении отрезка в заданном отношении в пространстве.
Пример.Даны точки 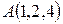 и
и 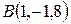 . Найти расстояние между этими точками и точку, которая делит отрезок
. Найти расстояние между этими точками и точку, которая делит отрезок 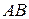 в отношении 2.
в отношении 2.
∆ Найдем расстояние между данными точками:
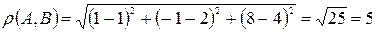 .
.
Пусть точка 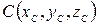 делит отрезок
делит отрезок 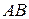 в отношении 2. Тогда получаем равенства:
в отношении 2. Тогда получаем равенства:
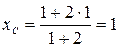 ,
,
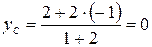 ,
,
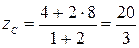 .
.
Таким образом, искомой точкой является точка 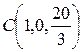 . ▲
. ▲
Геометрические векторы. Основные понятия. Линейные операции над векторами.
 Геометрическим вектором (или просто вектором) называется направленный отрезок.
Геометрическим вектором (или просто вектором) называется направленный отрезок.
В курсе линейной алгебры были рассмотрены «алгебраические» векторы, представляющие собой в 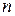 -мерном пространстве упорядоченные наборы
-мерном пространстве упорядоченные наборы 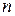 чисел. Там же отмечалось, что геометрические векторы (на плоскости или в трехмерном пространстве) являются частным случаем алгебраических векторов. Поэтому все результаты, известные из курса линейной алгебры для алгебраических векторов, переносятся и на случай геометрических векторов.
чисел. Там же отмечалось, что геометрические векторы (на плоскости или в трехмерном пространстве) являются частным случаем алгебраических векторов. Поэтому все результаты, известные из курса линейной алгебры для алгебраических векторов, переносятся и на случай геометрических векторов.
Будем обозначать вектор символом  , если известны начало – точка
, если известны начало – точка 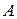 и конец – точка
и конец – точка 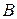 данного вектора. Если же начало и конец вектора неизвестны или не представляют интереса, то будем обозначать вектор символом
данного вектора. Если же начало и конец вектора неизвестны или не представляют интереса, то будем обозначать вектор символом 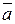 . На чертеже вектор будем изображать стрелкой. Длину вектора
. На чертеже вектор будем изображать стрелкой. Длину вектора 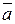 будем обозначать
будем обозначать 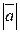 .
.
Начало вектора называется его точкой приложения.
Вектор называется нулевым, если его начало и конец совпадают. Нулевой вектор не имеет определенного направления и имеет длину, равную нулю.
Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых.
Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и одинаковое направление. Все нулевые векторы считаются равными. Из определения равенства векторов следует, что каковы бы ни были вектор 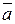 и точка
и точка 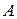 всегда можно найти такую точку
всегда можно найти такую точку 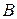 , что
, что 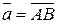 . Другими словами, любой вектор можно отложить из любой точки. В соответствии с этим геометрические векторы называют свободными (они определены с точностью до точки приложения).
. Другими словами, любой вектор можно отложить из любой точки. В соответствии с этим геометрические векторы называют свободными (они определены с точностью до точки приложения).
Два вектора называются противоположными, если они коллинеарны, имеют одинаковую длину и противоположные направления.
 В трехмерном пространстве векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
В трехмерном пространстве векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
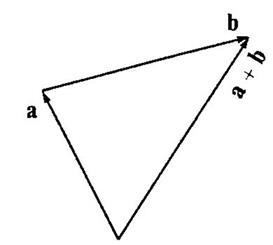
Введем линейные операции над векторами, т.е. операции сложения векторов и умножения вектора на действительное число.
Суммой 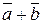 двух векторов
двух векторов 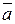 и
и  называется вектор, идущий из начала вектора
называется вектор, идущий из начала вектора 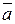 в конец вектора
в конец вектора  при условии, что вектор
при условии, что вектор  приложен к концу вектора
приложен к концу вектора 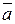 .
.
Произведением 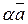 вектора
вектора 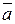 на действительное число
на действительное число 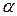 называется вектор, коллинеарный вектору
называется вектор, коллинеарный вектору 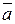 , имеющий длину
, имеющий длину 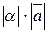 , и имеющий направление, совпадающее с направлением вектора
, и имеющий направление, совпадающее с направлением вектора  , если
, если 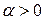 , и противоположное направлению вектора
, и противоположное направлению вектора 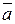 , если
, если 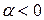 . Если
. Если 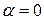 или
или 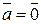 , то произведение
, то произведение 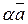 представляет собой нулевой вектор.
представляет собой нулевой вектор.
В курсе линейной алгебры были рассмотрены «алгебраические» векторы, представляющие собой в 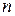 -мерном пространстве упорядоченные наборы
-мерном пространстве упорядоченные наборы 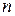 чисел и являющиеся элементами векторных пространств. Исходя из геометрических соображений, становится очевидным то, что введенные линейные операции над геометрическими векторами удовлетворяют всем аксиомам векторных пространств, а именно:
чисел и являющиеся элементами векторных пространств. Исходя из геометрических соображений, становится очевидным то, что введенные линейные операции над геометрическими векторами удовлетворяют всем аксиомам векторных пространств, а именно:
I) для любых векторов 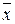 и
и 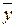 выполняется равенство:
выполняется равенство:
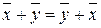 ;
;
II) для любых векторов 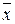 ,
, 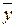 и
и 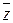 выполняется равенство:
выполняется равенство:
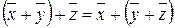 ;
;
III) существует нулевой вектор 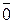 такой, что для любого вектора
такой, что для любого вектора 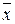 выполняется равенство:
выполняется равенство:
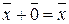 ;
;
IV) для любого вектора 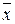 существует противоположный вектор
существует противоположный вектор 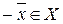 , удовлетворяющий равенству:
, удовлетворяющий равенству:
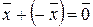 ;
;
V) для любого вектора 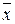 выполняется равенство:
выполняется равенство:
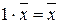 ;
;
VI) для любого вектора 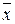 и любых чисел
и любых чисел 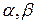 выполняется равенство:
выполняется равенство:
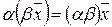 ;
;
VII) для любого вектора 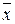 и любых чисел
и любых чисел 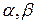 выполняется равенство:
выполняется равенство:
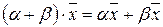 ;
;
VIII) для любых векторов 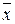 и
и 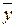 и любого числа
и любого числа 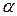 выполняется равенство:
выполняется равенство:
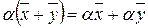 .
.
Таким образом, указанные аксиомы можно считать теперь свойствами геометрических векторов, и все результаты, известные из курса линейной алгебры для алгебраических векторов, переносятся и на случай геометрических векторов.
Справедливо следующее утверждение, являющееся критерием коллинеарности векторов.
Теорема.Ненулевые векторы 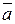 и
и  коллинеарны тогда и только тогда, когда существует действительное число
коллинеарны тогда и только тогда, когда существует действительное число 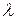 , такое что
, такое что 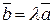 .
.
Доказательство. Достаточность этого утверждения сразу следует из определения произведения вектора на число.
Покажем, что из того, что 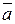 и
и  коллинеарны, следует, что существует действительное число
коллинеарны, следует, что существует действительное число 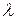 , такое что
, такое что 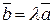 . Приложим векторы
. Приложим векторы 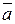 и
и  к общему началу
к общему началу 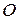 . Тогда эти векторы расположатся на одной прямой. Возможны два случая: 1) векторы
. Тогда эти векторы расположатся на одной прямой. Возможны два случая: 1) векторы 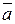 и
и  направлены в одну сторону; 2) указанные векторы противоположно направлены. Пусть
направлены в одну сторону; 2) указанные векторы противоположно направлены. Пусть 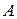 и
и 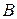 концы векторов
концы векторов 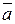 и
и  . Так как рассматриваемые векторы являются ненулевыми, то точки
. Так как рассматриваемые векторы являются ненулевыми, то точки 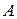 и
и 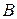 отличны от точки
отличны от точки 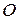 . Если точки
. Если точки 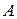 и
и 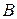 совпадают, то равны векторы
совпадают, то равны векторы 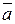 и
и  , и равенство
, и равенство 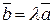 очевидно при
очевидно при 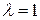 . Если же точки
. Если же точки 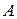 и
и 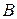 различны, то можно говорить о том, что точка
различны, то можно говорить о том, что точка 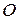 делит отрезок
делит отрезок 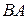 в некотором отношении, которое мы обозначим
в некотором отношении, которое мы обозначим 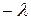 . Тогда справедливо равенство:
. Тогда справедливо равенство:
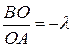 ,
,
Или, что то же самое,
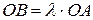 .
.
В случае, когда векторы 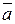 и
и  направлены в одну сторону, точка
направлены в одну сторону, точка 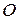 лежит вне отрезка
лежит вне отрезка 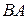 , и поэтому
, и поэтому 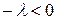 , т.е.
, т.е. 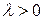 . Если же векторы
. Если же векторы 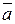 и
и  противоположно направлены, то точка
противоположно направлены, то точка 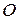 лежит внутри отрезка
лежит внутри отрезка 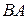 , и поэтому
, и поэтому 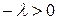 , т.е.
, т.е. 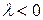 .
.
Покажем, что в обоих случаях 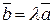 . Очевидно, что векторы
. Очевидно, что векторы  и
и 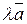 коллинеарны. Это следует из определения произведения вектора на число и коллинеарности векторов
коллинеарны. Это следует из определения произведения вектора на число и коллинеарности векторов 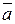 и
и  . Равенство длин векторов
. Равенство длин векторов  и
и 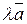 следует из соотношения
следует из соотношения 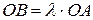 и определения произведения вектора на число. Векторы
и определения произведения вектора на число. Векторы  и
и 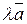 одинаково направлены, так как
одинаково направлены, так как 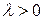 , если
, если 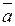 и
и  одинаково направлены, и
одинаково направлены, и 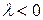 , если
, если 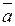 и
и  противоположно направлены. Таким образом,
противоположно направлены. Таким образом,
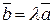 . ■
. ■
