Элементы линейной алгебры
Материалы установочной сессии по дисциплинам «Математика», «Высшая математика» для студентов сокращенной формы обучения 1-го курса всех специальностей на 2012-2013 уч. г.
СОДЕРЖАНИЕ:
- Краткий теоретический курс установочной сессии с примерами решения задач.
- Список литературы.
- Вопросы.
1. Элементы линейной алгебры.......................................................................
1.1. Понятие матрицы. Основные определения. Линейные действия над
матрицами. Умножение матриц..................................................................
1.2. Определители второго и третьего порядков.......................................
1.3. Свойства определителей.......................................................................
1.4. Сводная таблица основных методов решения определителей..........
1.5. Элементарные преобразования матрицы.............................................
1.6. Системы линейных алгебраических уравнений..................................
Решение систем линейных алгебраических уравнений
по формулам Крамера..........................................................................
Матричная запись СЛАУ и ее решение с помощью обратной матрицы.................................................................................................
Ранг матрицы и его свойства...............................................................
Исследование систем линейных уравнений.......................................
1.7. Сводная таблица для исследования систем линейных уравнений...
Примеры решения практических задач......................................................
Элементы линейной алгебры
1.1.Понятие матрицы. Основные определения
Определение. Прямоугольная таблица из m×n действительных чисел вида
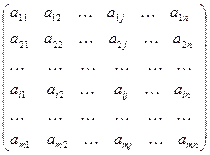
называется матрицей типа m×n. Числа аij, входящие в состав данной матрицы, называются ее элементами; первый индекс i – номер строки, второй индекс j –номер столбца, на пересечении которых находится данный элемент.
Обозначают матрицы большими буквами латинского алфавита А, В, С, … и ограничивают справа и слева либо круглыми скобками 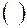 , либо двойными вертикальными чертами
, либо двойными вертикальными чертами  , либо квадратными скобками
, либо квадратными скобками 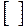 .
.
Употребляются и более краткие обозначения матрицы: 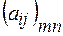 ,
, 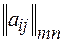 ,
, 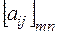 . Если необходимо указать только размеры матрицы А, то пишут
. Если необходимо указать только размеры матрицы А, то пишут 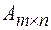 или
или 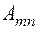 .
.
Определение. Матрица, у которой m ¹ n, называется прямоугольной.
Например, 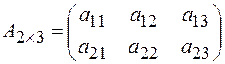 .
.
Определение.Матрица, у которой m = n, называется квадратной матрицей n – го порядка.
Например, матрицы (а1), 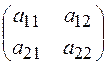 и т. д. являются квадратными матрицами соответственно первого, второго и т. д. порядков.
и т. д. являются квадратными матрицами соответственно первого, второго и т. д. порядков.
Определение. Матрица размера 1 ´ n называется матрицей – строкой. При записи матрицы – строки первый индекс не пишут:
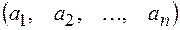 .
.
Определение. Матрица размера m ´ 1 называется матрицей - столбцом. При записи матрицы – столбца второй индекс не пишут:
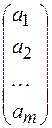 .
.
В случае квадратной матрицы вводятся понятия главной и побочной (дополнительной) диагоналей.
Определение. Элементы а11, а22, …, апп (i = j), стоящие на диагонали, идущей из левого верхнего угла в правый нижний угол, т. е. , образуют главную диагональ матрицы. Элементы а1п, а2п–1, …, ап1, стоящие на диагонали, идущей из правого верхнего угла в левый нижний угол , образуют побочную или дополнительную диагональ.
Определение. Если в матрице элементы по одну сторону от главной диагонали равны нулю, а по другую отличны от нуля, то матрица называется треугольной. Например,
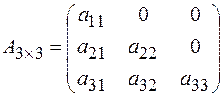 или
или 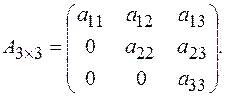
Определение. Если в квадратной матрице все элементы, кроме элементов главной диагонали, равны нулю, то матрица называется диагональной:
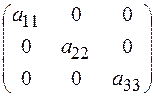 .
.
Определение 9. Если в диагональной матрице все элементы главной диагонали равны единице, то она называется единичной и обозначается Е.
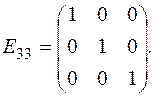
Определение. Матрица, все элементы которой равны нулю, называется нуль–матрицей.
Единичная матрица и нуль–матрица в линейной алгебре играют ту же роль, что 0 и 1 в арифметике.
Определение. Матрицы А и В называются равными, если они имеют одинаковую размерность и соответствующие элементы этих матриц равны, т. е. А = В, если А = (аij)m×n, В = (bij)m×n и aij = bij ( 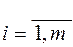 ;
; 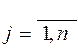 ).
).
Определение.Пусть А = (аij)m×n. Если заменить в матрице А строки соответственно столбцами, а столбцы строками, то полученная матрица АТ = (аji)n×m называется транспонированной к данной, а процесс ее получения транспонированием. Например:
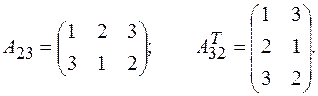
Определение.Линейными действиями над матрицами называются сложение и вычитание матриц, умножение матрицы на число.
Действия сложения и вычитания возможны только над матрицами одной и той же размерности.
Определение. Суммой (разностью) двух матриц А = (аij)mn и В = (bij)mn называется третья матрица С = (сij)mn, каждый элемент которой равен сумме (разности) соответствующих элементов матриц А и В, т. е.
С = А ± В = (аij ± bij)mn.
Операция сложения матриц обладает следующими свойствами:
1. А + В = В + А.
2. А + 0 = А.
3. (А + В) + С = А + (В + С).
4. А + (– А) = 0.
5. (А + В)Т = АТ + ВТ.
Определение. Чтобы умножить матрицу на число α ¹ 0, нужно умножить на это число каждый элемент матрицы А, т. е.
α∙А = (α∙аij)m×n.
Произведение матрицы на число обладает следующими свойствами:
1. α∙А = А∙α.
2. α∙(β∙А) = (α∙β)∙А.
3. (α + β) А = α∙А + β∙А.
4. α∙(А + В) = α∙А + α∙В.
Определение. Произведением матрицы А = (аij)mn на матрицу В = (bjk)np называется такая матрица С = (сik)mp, каждый элемент которой сik равен сумме произведений элементов i-той строки матрицы А на соответствующие элементы k–того столбца матрицы В, т. е.
сik = ai1∙b1k + ai2∙b2k + … + aij∙bjk + … + ain∙bnk.
Из определения следует, что матрица-произведение содержит строк столько, сколько их в матрице А, а столбцов – сколько в матрице В.
Умножение матрицы на матрицу не всегда выполнимо. Две матрицы можно перемножить только тогда, когда число столбцов первой матрицы равно числу строк второй матрицы. Схематически это можно записать так 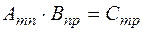 .
.
Произведение двух матриц А и В обозначаются символом А∙В,
например:
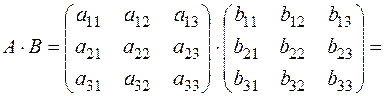
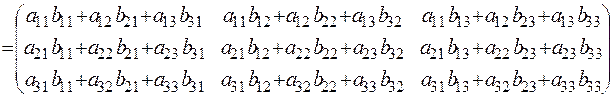
По отношению к произведению двух матриц переместительный закон, вообще говоря, не выполняется: А∙В ¹ В∙А.
Действие умножения матриц обладает следующими свойствами:
1. А∙В∙С = (А∙В)∙С = А∙(В∙С).
2. (А + В)∙С = А∙С + В∙С.
3. А∙Е = Е∙А = А.
4. (А∙В)Т = ВТ∙АТ.
Определение. Матрицы, для которых выполняется условие А∙В = В∙А, называются перестановочными (коммутативными).
