Производная обратной функции
Пусть y = f(x) – непрерывная и возрастающая на [a; b]. Значит, на этом промежутке она имеет обратную функцию 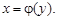
Теорема. Если функция y = f(x) определена, непрерывна и монотонна на [a; b] и в точке 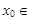 [a; b] имеет производную
[a; b] имеет производную 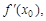 то обратная функция x = j(y) имеет производную в точке y0 = f(x0) которую можно найти по формуле
то обратная функция x = j(y) имеет производную в точке y0 = f(x0) которую можно найти по формуле 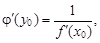 т. е. производная обратной функции равна обратной величине производной данной функции.
т. е. производная обратной функции равна обратной величине производной данной функции.
Пример 6. Пользуясь правилом дифференцирования обратной функции, найти производную 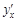 для функции
для функции 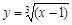 .
.
Решение
Находим обратную функцию. Так как 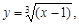 то y3 = x – 1. Значит,
то y3 = x – 1. Значит, 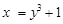 . Обратная функция
. Обратная функция 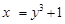 имеет производную
имеет производную 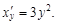 Следовательно,
Следовательно, 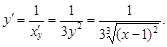
Логарифмическое дифференцирование
В ряде случаев для нахождения производной целесообразно заданную функцию сначала прологарифмировать, а затем результат продифференцировать. Такую операцию называют логарифмическим дифференцированием.
Пример 7. Найти производную функции 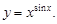
Решение
Логарифмируя данное равенство по основанию e, получаем 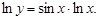 Дифференцируя полученное равенство, находим
Дифференцируя полученное равенство, находим
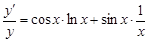 , откуда
, откуда 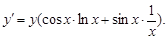
Подставляем 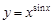 и получаем
и получаем 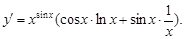
Дифференцирование неявных функций
Если функция задана уравнением y = f(x), разрешенным относительно y, то функция задана в явном виде.
Под неявным заданием функции понимают задание функции в виде уравнения F(x; y) = 0, неразрешенного относительно y. Например,
y + 2x + cos y – 1 = 0 или 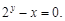
Для нахождения производной неявной функции необходимо продифференцировать это уравнение по x, рассматривая при этом y как функцию x, и затем полученное уравнение разрешить относительно 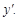
Пример 8. Найти производную функции y, заданную уравнением 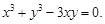
Решение
Функция у задана неявно. Дифференцируем по x равенство x3 + y3 –
– 3xy = 0
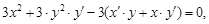
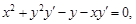
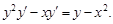
Из последнего соотношения следует, что 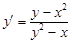 .
.
Производная высших порядков
Производная 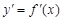 функции y = f(x) есть также функция x и называется производной первого порядка.
функции y = f(x) есть также функция x и называется производной первого порядка.
Если функция 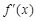 дифференцируема, то ее производная называется производной второго порядка и обозначается
дифференцируема, то ее производная называется производной второго порядка и обозначается 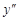 или
или 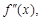
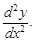
Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается 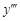 или
или 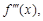
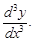
Производной n-го порядка (или n-й производной) называется производная от производной (n –1) порядка: 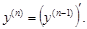
Производные порядка выше первого называются производными высших порядков.
Пример 9.Найти вторую производную функции 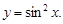
Решение
Находим первую производную функции
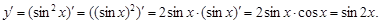
Дифференцируем еще раз
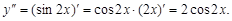
Тест 5.Производная третьего порядка функции 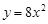 равна:
равна:
1) 16x;
2) (16х)3;
3) 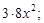
4) 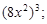
5) 0.
