Производная обратной функции

Билет 1

Производная. Определение, непрерывность функции, имеющей производную.

Определение: Производной от функции 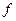в точке 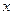называется предел, к которому стремится отношение ее приращения 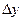в этой точке к соответствующему приращению 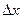аргумента, когда последнее стремится к нулю:

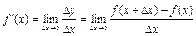
Т.е., если 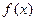определена в 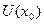, то

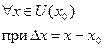
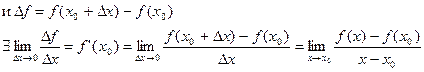
Теорема: (необходимое условие существования производной)

Если функция 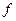имеет конечную 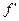в точке 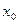, то 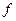непрерывна в точке .

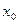Доказательство:

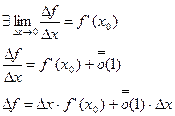
При ,

Следовательно 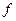- непрерывна в точке .

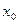Теорема доказана.

Замечание: обратное утверждение неверно, если функция 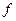непрерывна в точке 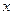, то отсюда не следует, что она имеет производную в этой точке.

Контрпример: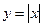

Утверждение: если функция имеет в точке правую и левую производную, то она непрерывна и справа и слева.

Контрпример:

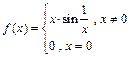
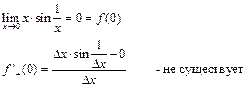
Билет 2

Геометрический смысл производной.

Теорема 1:

График функции имеет невертикальную касательную тогда и только тогда, когда существует конечное значение производной этой функции в данной точке.

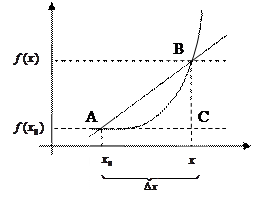
Доказательство:

Пусть существует значение f’( 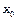)-конечное, тогда

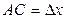
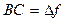
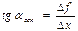
при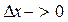

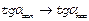
Секущая стремится к касательной.

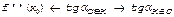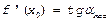=> ч.т.д.

Пусть существует невертикальная касательная => существует 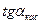- конечный.

Секущая стремится к касательной.

=>

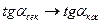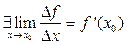
Теорема доказана.

Билет 3

Арифметические свойства производной.

Пусть f = f(x) и g = g(x) – функции, имеющие конечные производные в точке x₀, тогда справедливы равенства:

1.

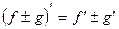
2.

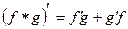
2.1. 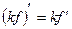где k – константа

3.

-----------------------------------------------------------------------------------------------------------------------------

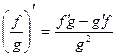
1.

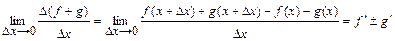
2.

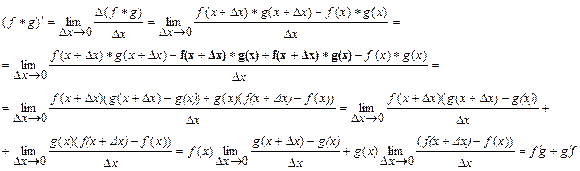
Заметим, что функция f , как имеющая производную, непрерывна, и потому при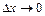

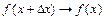
3.

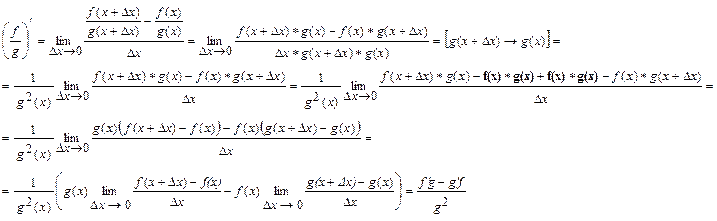
Билет 4

Производная обратной функции.

Определение: Пусть на интервале (a,b) задана непрерывная строго монотонная, т.е. строго возрастающая или строго убывающая, функция 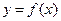. Пусть образ (a,b) есть интервал (A,B). тогда обратная к 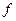функция 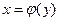есть однозначная непрерывная и строго монотонная на (A,B) функция.

Зафиксируем 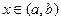и дадим ему приращение 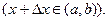Тогда 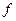получит соответствующее приращение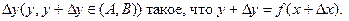

Наоборот,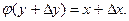

Вследствие непрерывности прямой и обратной функций для указанных 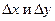имеет место утверждение: из 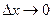следует 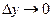, и обратно.

Пусть теперь функция 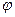в точке у имеет неравную нулю производную 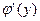. Покажем, что в таком случае функция 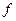также имеет в соответствующей точке х производную. В самом деле,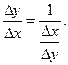

Так как из того, что 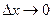следует, ч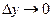то , то

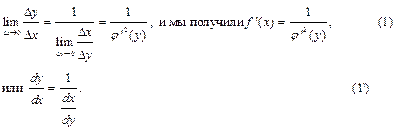
Этим доказано, что если 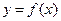есть строго монотонная непрерывная функция и 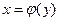обратная к ней функция, имеющая в точке у производную 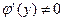, то функция 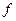имеет в соответствующей точке х производную, определяемую формулой (1).

Может случится, что в точке 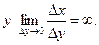В этом случае, очевидно, функция 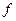имеет в соответствующей точке х производную .

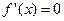Если же 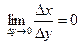, то для строго возрастающей функции при этом 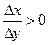, а для строго убывающей 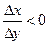. В первом случае 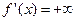, а во втором .

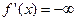Пример 1.

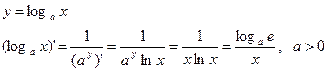
Если логарифм натуральный, то

.

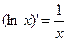Функция ln x как действительная функция определена только для положительных значений х.

Пример 2.

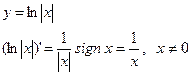
где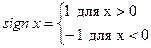

Пример 3.

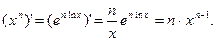
Пример 4.

Функция 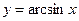строго возрастает на отрезке [-1,1] и отображает этот отрезок на 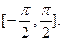Обратная к ней функция 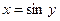имеет производную 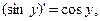положительную на интервале 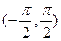. Поэтому

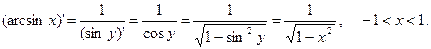
Пример 5.

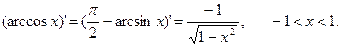
Пример 6.

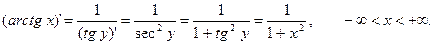
Билет 5