Численное решение алгебраических уравнений. Метод Ньютона

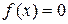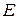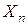Пусть требуется решить уравнение с точностью и - приближенное значение корня. Воспользуемся формулой:

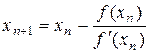. (1)

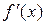Если и 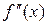сохраняют свой знак в окрестности корня уравнения (строго положительны или строго отрицательны), то 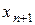расположено ближе к корню, чем .

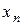Циклическое повторение вычислений по формуле (1) при использовании на каждом последующем этапе найденного приближенного значения корня позволит вычислить корень со сколь угодно высокой точностью. Вычисления прекращаются, когда разность между соседними приближениями станет меньше Е. Данный метод решения уравнений называется методом Ньютона.

Пример 2. Найти корень уравнения 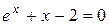с точностью до 0,01 методом Ньютона.

Используя графический метод (см. рис. 2), видим, что корень уравнения расположен на интервале (0;1)

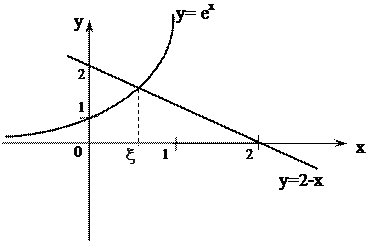Рис. 2

В заданном уравнении 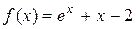, 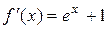. Формула (1) для него имеет вид

.

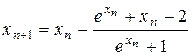Из предыдущего примера известно, что корень уравнения расположен на интервале (0,1). Примем за начальное приближение 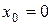. Повторяя процесс вычислений, получим следующие значения

,

,

.

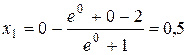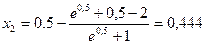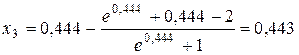Так как 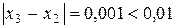, то процесс вычислений заканчиваем, и корень уравнения считаем равным 0,443.

Модифицированный метод Ньютона.

Точность в определении корня также может быть повышена следующим образом. Воспользуемся формулой:

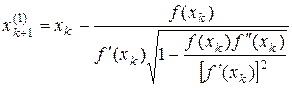. (2)

Вычисление корня итерационным методом с использованием формулы (2) называют модифицированным методом Ньютона.

В случае модифицированного метода Ньютона скорость сходимости на порядок выше, чем в методе Ньютона.

Если 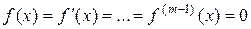, то говорят, что корень 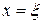имеет кратность т. Кратный корень уравнения может быть найден, если вместо исходного уравнения 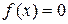метод Ньютона применить к уравнению 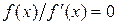, которое имеет тот же корень кратностью 1. После преобразований приходим к формуле

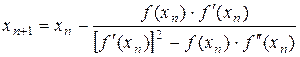. (3)

Формулу (3.11) рекомендуется применять при медленной сходимости метода Ньютона, когда есть подозрение на наличие кратного корня. В тех случаях, когда кратность корня заранее известна, он может быть найден по более простой итерационной формуле

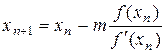, (4)

где т - кратность корня.

Формулы (1), (2), (3) и (4) могут быть использованы для вычисления как действительных, так и комплексных корней уравнений. В последнем случае начальное приближение корня является комплексным числом.

Выводы.

Сравнение методов численного решения уравнений, рассмотренных в вопрос е 2-3, с методом бисекций показывает гораздо более быструю сходимость метода Ньютона и его модификации. Это достигается за счёт использования свойств функции. Однако следует иметь в виду, что в методе Ньютона налагаются более жёсткие условия на функцию – требование дифференцируемости, сохранение знака f(x) и 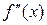в окрестности корня.