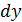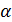Связь непрерывности и дифференцируемости
Мы познакомились с двумя свойствами функции в точке – непрерывность и дифференцируемость. Какое свойство сильнее?
Теорема. Если функция дифференцируема в точке, то она в ней и непрерывна.
Доказательство. Пусть функция 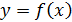 в точке
в точке 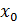 дифференцируема, т.е. существует конечное число
дифференцируема, т.е. существует конечное число 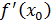 :
:
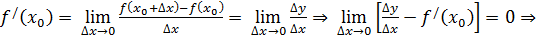
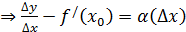 - б.м. при
- б.м. при 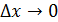 ,
, 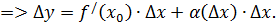 Если
Если 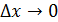 , то
, то 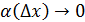 , тогда
, тогда 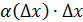 также стремится к нулю, причём
также стремится к нулю, причём
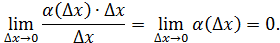
В таком случае говорят, что 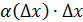 является бесконечно малой более высокого порядка малости по сравнению с
является бесконечно малой более высокого порядка малости по сравнению с 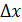 и этот факт обозначается так:
и этот факт обозначается так: 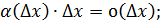 читается:
читается: 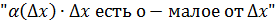 . Итак
. Итак
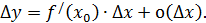 (1)
(1)
Эта формула показывает структуру приращения функции.Отсюда следует, что если 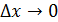 , то
, то 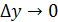 - бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, а это есть третья формулировка определения непрерывности функции в точке (см. п.8,3,формула (4)). Итак, свойство дифференцируемости сильнее – непрерывность из него следует автоматически (по теореме). А наоборот? Оказывается, что если функция непрерывна в точке, то она не обязательно дифференцируема.
- бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, а это есть третья формулировка определения непрерывности функции в точке (см. п.8,3,формула (4)). Итак, свойство дифференцируемости сильнее – непрерывность из него следует автоматически (по теореме). А наоборот? Оказывается, что если функция непрерывна в точке, то она не обязательно дифференцируема.
Пример 6. Рассмотрим функцию 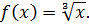
Производная этой функции 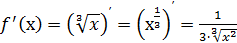 . Она равна
. Она равна 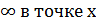 =0, т.к. tg
=0, т.к. tg  =
= 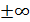 , то касательная вэтой точке перпендикулярна оси ох. Для функции у=
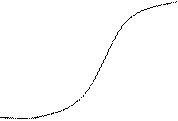
, то касательная вэтой точке перпендикулярна оси ох. Для функции у= 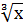 в начале координат касательной является ось oу (см.рис.3). Производная в начале координат не существует -функция не дифференцируемая в этой точке, но непрерывна.
в начале координат касательной является ось oу (см.рис.3). Производная в начале координат не существует -функция не дифференцируемая в этой точке, но непрерывна.


 1
1
 |
-1 1
 -1
-1
Рис. 3
Дифференциал функции.
Вернёмся к рассуждениям, приводимых при определении производной. Пусть имеется функция 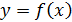 . Воспользуемся формулой (1), показывающей структуру приращения функции:
. Воспользуемся формулой (1), показывающей структуру приращения функции: 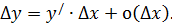 Эта формула показывает, что приращение функции состоит из двух частей. Первая часть,
Эта формула показывает, что приращение функции состоит из двух частей. Первая часть, 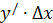 , линейна относительно приращения аргумента
, линейна относительно приращения аргумента 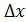 . Вторая часть,
. Вторая часть, 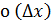 – о – малое от
– о – малое от 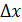 , является бесконечно малой более высокого порядка малости по сравнению с
, является бесконечно малой более высокого порядка малости по сравнению с 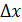 . Отсюда следует, что основной «вес» приращения функции приходится на первое слагаемое. По этой причине оно называется главной частью приращения функции.
. Отсюда следует, что основной «вес» приращения функции приходится на первое слагаемое. По этой причине оно называется главной частью приращения функции.
Определение. Главная часть приращения функции, линейная относительно приращения аргумента 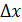 , называется дифференциалом функции и обозначается
, называется дифференциалом функции и обозначается 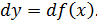 Итак, по определению
Итак, по определению
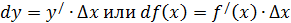 (2)
(2)
Пример 7. 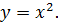 Тогда
Тогда 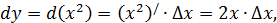
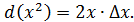
Пример 8. 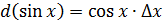 .
.
Пример 9. 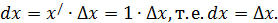
Таким образом, дифференциал независимого аргумента равен его приращению. С учётом этого равенства формула для дифференциала функции принимает «симметричный» вид: 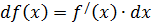 или
или
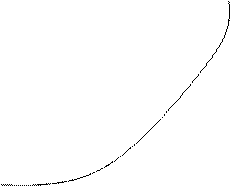
 Отсюда, в частности, следует, что
Отсюда, в частности, следует, что 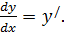 Таким образом, становится понятным введённое ранее для
Таким образом, становится понятным введённое ранее для 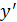 обозначение
обозначение 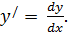 Также ясно, что нахождение дифференциала функции сводится к нахождению её производной, которую надо формально умножить на
Также ясно, что нахождение дифференциала функции сводится к нахождению её производной, которую надо формально умножить на 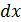 .
.
 Обратимся теперь к геометрическому смыслу дифференциала функции в точке
Обратимся теперь к геометрическому смыслу дифференциала функции в точке
.
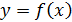













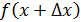
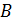
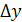
|










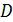













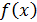 A
A 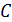
|
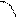





 0
0 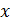
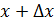
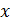
Рис. 4
Возьмём произвольную точку 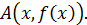 Дадим приращение
Дадим приращение 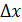 , получим новую точку
, получим новую точку 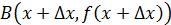 и приращение функции
и приращение функции
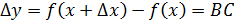 (рис. 4). По определению
(рис. 4). По определению 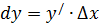 или
или
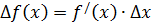 . Исходя из геометрического смысла производной она равна тангенсу угла наклона касательной к кривой в точке
. Исходя из геометрического смысла производной она равна тангенсу угла наклона касательной к кривой в точке 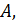 т.е.
т.е. 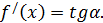 Тогда из
Тогда из 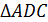 следует, что
следует, что 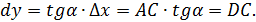
Из рис. 4 видно, что если, получив приращение 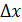 , двигаться по кривой, то придём в точку
, двигаться по кривой, то придём в точку 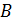 и получим приращение
и получим приращение 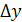 . Если же, получив приращение
. Если же, получив приращение 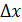 , двигаться по касательной к кривой в точке
, двигаться по касательной к кривой в точке 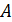 , то придём в точку
, то придём в точку 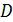 и получим приращение
и получим приращение 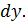 В этом и состоит геометрический смысл: дифференциал функции в точке представляет собой приращение ординаты касательной к кривой в этой точке.
В этом и состоит геометрический смысл: дифференциал функции в точке представляет собой приращение ординаты касательной к кривой в этой точке.