Основные теоремы дифференциального исчисления
Знание производной некоторой функции позволяет делать заключение о поведении самой функции. В основе различных приложений понятия производной лежат несколько теорем, называемых основными теоремами дифференциального исчисления.
Теорема(теорема Ферма*).
Пусть функция 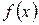 определена на интервале
определена на интервале 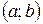 и в некоторой точке
и в некоторой точке 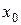 этого интервала имеет наибольшее или наименьшее значение. Тогда, если в точке
этого интервала имеет наибольшее или наименьшее значение. Тогда, если в точке 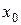 существует производная, то она равна нулю, т.е.
существует производная, то она равна нулю, т.е. 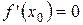 .
.
 |
Рис. 4.2
Геометрически это означает, что в точке с абсциссой 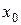 (
( 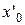 ) касательная к графику функции
) касательная к графику функции 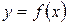 параллельна оси Ох (рис. 4.2).
параллельна оси Ох (рис. 4.2).
Теорема(теорема Ролля*).
Если функция 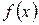
1) определена и непрерывна на отрезке 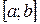 ;
;
2) имеет производную на интервале 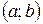 ;
;
3) на концах отрезка 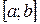 принимает равные значения, т.е.
принимает равные значения, т.е. 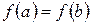 ,
,
то в интервале 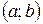 существует, по крайней мере, одна точка с, в которой производная данной функции равна нулю, т.е.
существует, по крайней мере, одна точка с, в которой производная данной функции равна нулю, т.е. 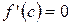 .
.
Геометрический смысл теоремы состоит в том, что на графике функции 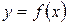 найдется точка, в которой касательная к графику параллельна оси Ох (рис.4.3).
найдется точка, в которой касательная к графику параллельна оси Ох (рис.4.3).
 |
Рис. 4.3
Теорема(теорема Лагранжа*).
Если функция 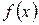
1) непрерывна на отрезке 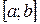 ;
;
2) имеет производную 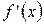 на интервале
на интервале 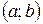 ,
,
то в интервале 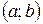 существует, по крайней мере, одна точка с такая, что справедлива формула
существует, по крайней мере, одна точка с такая, что справедлива формула
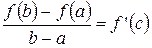
или
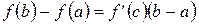 .
.
Последнее равенство читается так: приращение функции на интервале равно произведению производной в некоторой внутренней точке интервала на приращение независимой переменной.
Эту формулу называют формулой конечных приращений.
Теорема(теорема Коши*).
Если функции 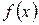 и
и 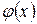
1) непрерывны на отрезке 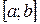 ;
;
2) имеют производные 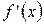 и
и 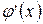 на интервале
на интервале 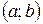 ;
;
3) производная 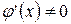 на интервале
на интервале 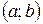 ,
,
то в интервале 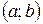 существует, по крайней мере, одна точка с такая, что справедлива формула
существует, по крайней мере, одна точка с такая, что справедлива формула
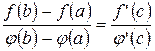 .
.
Теорема Коши устанавливает связь между приращениями функций на некотором отрезке и значениями их производных в некоторой точке, лежащей внутри этого отрезка.
4.18. Правило Лопиталя*для раскрытия неопределенностей
Рассмотрим способ раскрытия неопределенностей при помощи производных. Этот способ обычно называют «Правилом Лопиталя».
Напомним, что под неопределенностями понимают неопределенные выражения вида: 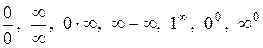 , встречающиеся при вычислении пределов функций. Некоторые элементарные приемы раскрытия неопределенностей были даны (п.2.13).
, встречающиеся при вычислении пределов функций. Некоторые элементарные приемы раскрытия неопределенностей были даны (п.2.13).
Теперь, опираясь на теорему Коши, введем правило Лопиталя для раскрытия неопределенностей типа 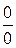 и
и 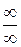 , которые являются основными видами неопределенностей.
, которые являются основными видами неопределенностей.
Неопределенность вида 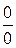
Теорема(правило Лопиталя).
Пусть функции 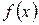 и
и 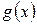 определены и дифференцируемы в некоторой окрестности точки
определены и дифференцируемы в некоторой окрестности точки 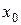 , за исключением, быть может, самой точки
, за исключением, быть может, самой точки 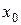 . Пусть
. Пусть 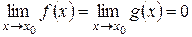 и
и 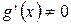 в указанной окрестности точки
в указанной окрестности точки 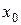 . Тогда, если существует (конечный или бесконечный) предел
. Тогда, если существует (конечный или бесконечный) предел
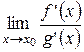 ,
,
то существует и предел 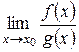 , причем справедлива формула
, причем справедлива формула
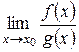 =
= 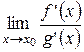 .
.
Теорема дает правило, сводящее вычисление предела отношения двух функций к вычислению предела отношения их производных.
Замечания.
1. Если производные 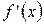 и
и  удовлетворяют тем же требованиям, что и сами функции
удовлетворяют тем же требованиям, что и сами функции 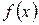 и
и 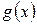 , то правило Лопиталя можно применять повторно.
, то правило Лопиталя можно применять повторно.
Получим при этом
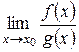 =
= 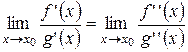 .
.
2. При вычислении предела отношения производных допустимы различные упрощения полученных выражений, сокращение общих множителей, использование уже известных пределов.
3. Теорема справедлива и в случае, когда 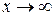 (
( 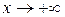
или 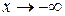 ).
).
Пусть требуется найти 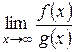 , если
, если 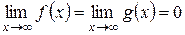 .
.
Сделаем подстановку 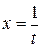 . Тогда, если
. Тогда, если 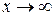 , то
, то 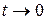 . Имеем
. Имеем
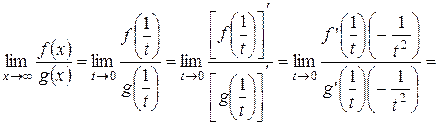
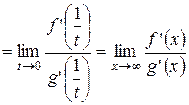 .
.
Примеры
Найти пределы функций:
1. 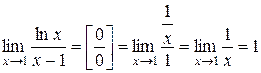 .
.
2. 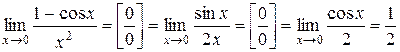 .
.
3. 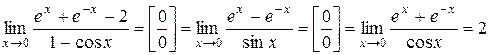 .
.
4. 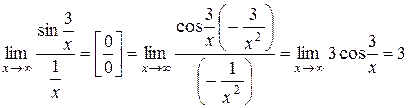 .
.
Неопределенность вида 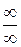
Теорема(правило Лопиталя).
Пусть функции 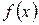 и
и 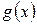 определены и дифференцируемы в некоторой окрестности точки
определены и дифференцируемы в некоторой окрестности точки 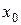 ,кроме, быть может, самой точки
,кроме, быть может, самой точки 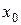 . Пусть
. Пусть 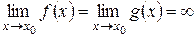 и
и 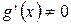 в указанной окрестности точки
в указанной окрестности точки 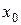 . Тогда, если существует (конечный или бесконечный) предел
. Тогда, если существует (конечный или бесконечный) предел
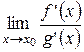 ,
,
то существует и предел 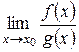 , причем справедлива формула
, причем справедлива формула
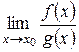 =
= 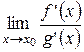 .
.
Замечания, сделанные для первой теоремы справедливы и для второй теоремы.
Примеры
Найти пределы функций:
1. 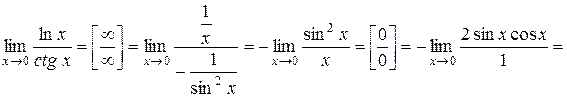
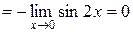 .
.
2. 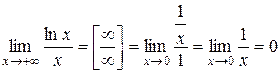 .
.
3. 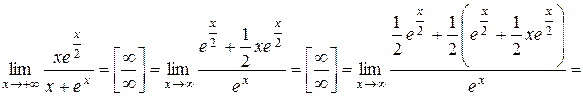
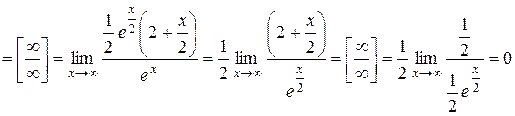 .
.
Чтобы раскрыть неопределенности видов 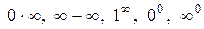 , их путем алгебраических преобразований сводят к неопределенностям типа
, их путем алгебраических преобразований сводят к неопределенностям типа 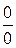 или
или 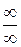 , после чего применяют правило Лопиталя.
, после чего применяют правило Лопиталя.
Неопределенность вида 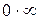
Пусть 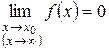 и
и 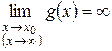 . Требуется найти
. Требуется найти 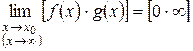 .
.
Перепишем искомое выражение в виде
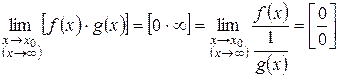
или
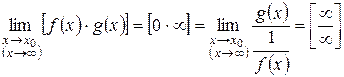
и применим правило Лопиталя.
Примеры
Найти пределы функций:
1. 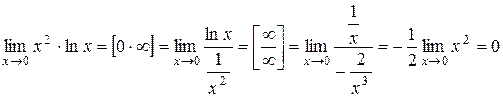 .
.
2. 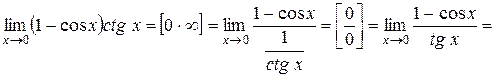
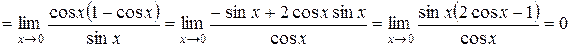 .
.
Неопределенность вида 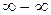
Пусть 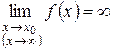 ,
, 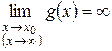 .
.
Тогда 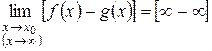 .
.
Сводим данное выражение к неопределенности 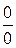 :
:
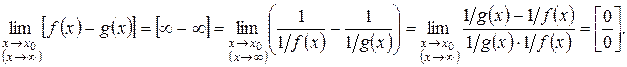
Примеры
Найти пределы функций:
1. 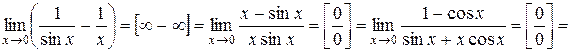
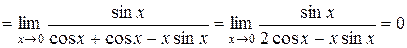 .
.
2. 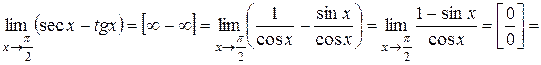
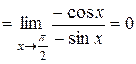 .
.
Неопределенности видов 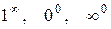
Такие неопределенные выражения возникают при вычислении пределов показательно-степенной функции
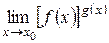
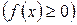 ,
,
когда имеет место один из трех случаев:
а) 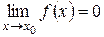 ,
, 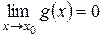 ;
;
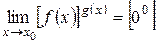 ;
;
б) 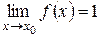 ,
, 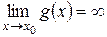 ;
;
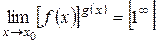 ;
;
в) 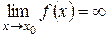 ,
, 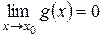 ;
;
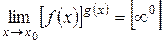 .
.
В этих случаях поступают следующим образом:
1) логарифмируют функцию, стоящую под знаком предела,
т.е., если
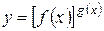 ,
,
то
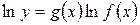 ;
;
2) вычисляют предел 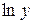
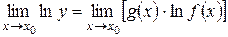 .
.
Предел 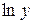 представляет собой неопределенность уже изученного типа
представляет собой неопределенность уже изученного типа 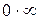 . Ее раскрываем сведением к неопределенностям вида
. Ее раскрываем сведением к неопределенностям вида 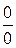 или
или 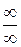 и применяем правило Лопиталя.
и применяем правило Лопиталя.
Следует заметить, что вычисляется предел не от заданной функции, а от ее логарифма.
3) Находят предел функции у.
Пусть 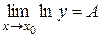 или
или 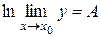 (в силу непрерывности логарифмической функции).
(в силу непрерывности логарифмической функции).
Тогда
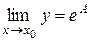 ,
,
т.е.
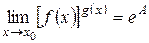 .
.
Примеры
Найти пределы функций:
1. 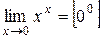
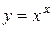 ;
; 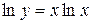 ;
;
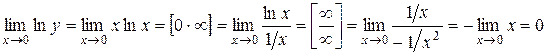 .
.
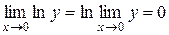 ;
;
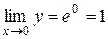 ;
; 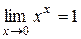 .
.
2. 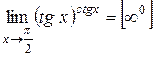 .
.
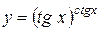 ;
; 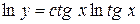 ;
;
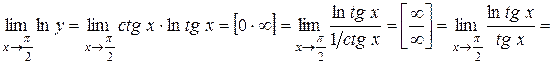
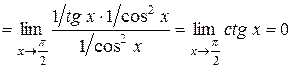 ;
;
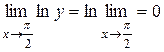 ;
;
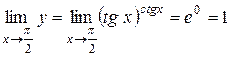 .
.
3. 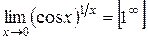 .
.
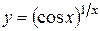 ;
; 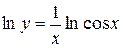 ;
;
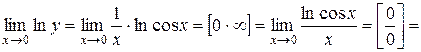
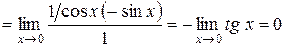 ;
;
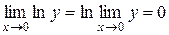 ;
;
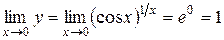 .
.
Упражнения
Пользуясь основными правилами дифференцирования, найти производные функций:
| 1. | 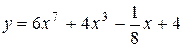 ; ; | 2. | 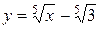 ; ; |
| 3. | 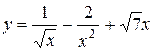 ; ; | 4. | 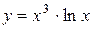 ; ; |
| 5. | 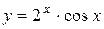 ; ; | 6. | 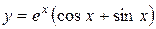 ; ; |
| 7. | 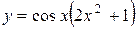 ; ; | 8. | 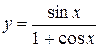 ; ; |
| 9. | 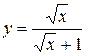 ; ; | 10. | 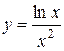 ; ; |
| 11. | 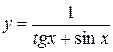 | 12. | 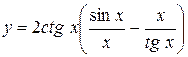 . . |
Применив правило дифференцирования сложной функции, найти производные функций:
| 13. | 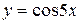 ; ; | 14. | 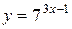 ; ; |
| 15. | 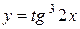 ; ; | 16. | 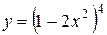 ; ; |
| 17. | 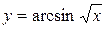 ; ; | 18. | 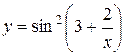 ; ; |
| 19. | 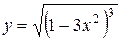 ; ; | 20. | 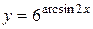 ; ; |
| 21. | 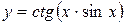 ; ; | 22. | 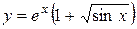 ; ; |
| 23. | 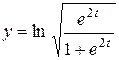 ; ; | 24. | 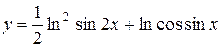 . . |
Найти производные для функций, заданных параметрически:
| 25. | 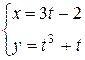 ; ; | 26. | 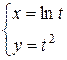 ; ; |
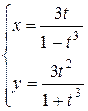 ; ; | 28. | 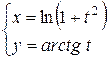 . . |
Найти производные указанных порядков для функций:
| 29. | 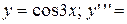 ? ? | 30. | 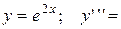 ? ? |
| 31. | 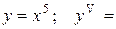 ? ? | 32. | 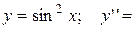 ? ? |
Найти дифференциалы функций:
| 33. | 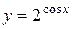 ; ; | 34. | 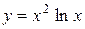 ; ; |
| 35. | 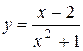 ; ; | 36. | 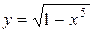 . . |
Найти пределы функций, используя правило Лопиталя:
| 37. | 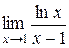 ; ; | Ответ: 1; |
| 38. | 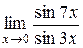 ; ; | Ответ: 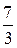 ; ; |
| 39. | 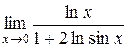 ; ; | Ответ: 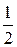 ; ; |
| 40. | 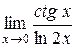 ; ; | Ответ: 0; |
| 41. | 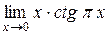 ; ; | Ответ: 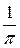 ; ; |
| 42. | 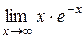 ; ; | Ответ: 0; |
| 43. | 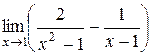 ; ; | Ответ: 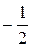 ; ; |
| 44. | 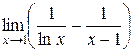 ; ; | Ответ: 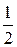 ; ; |
| 45. | 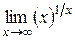 ; ; | Ответ: 1; |
| 46. | 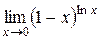 ; ; | Ответ: 1; |
| 47. | 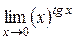 ; ; | Ответ: 1. |
* П.Ферма (1601−1665) – французский математик.
* М.Ролль (1652−1719) – французский математик.
* Ж.Лагранж (1736−1813) – французский математик.
* О.Коши (1789−1859) – французский математик.
* Г.Лопиталь (1661−1704) – французский математик.
