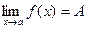Матрицы линейных преобразований

Пусть в n- мерном линейном пространстве с базисом , ,…, задано линейное преобразование А. Тогда векторы А ,А ,…,А - также векторы этого пространства и их можно представить в виде линейной комбинации векторов базиса:

A = a₁₁ + a₂₁ +…+ a_n1

A = a₁₂ + a₂₂ +…+ a_n2

……………………………….

A = a_n1 + a_n2 +…+ a_nn

Тогда матрица А = 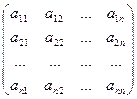называется матрицей линейного преобразования А.

Если в пространстве L взять вектор = x₁ + x₂ +…+ x_n , то A Î L.

, где

……………………………..

Эти равенства можно назвать линейным преобразованием в базисе , ,…, .

В матричном виде:

, А× ,

Пример. Найти матрицу линейного преобразования, заданного в виде:

x¢ = x + y

y¢ = y + z

z¢ = z + x

x¢ = 1×x + 1×y + 0×z

y¢ = 0×x + 1×y + 1×z

z¢ = 1×x + 0×y + 1×z

A =

На практике действия над линейными преобразованиями сводятся к действиям над их матрицами.

Определение: Если вектор переводится в вектор линейным преобразованием с матрицей А, а вектор в вектор линейным преобразованием с матрицей В, то последовательное применение этих преобразований равносильно линейному преобразованию, переводящему вектор в вектор (оно называется произведением составляющих преобразований).

С = В×А

Пример. Задано линейное преобразование А, переводящее вектор в вектор и линейное преобразование В, переводящее вектор в вектор . Найти матрицу линейного преобразования, переводящего вектор в вектор .

С = В×А

Т.е.

Примечание: Если ïАï= 0, то преобразование вырожденное, т.е., например, плоскость преобразуется не в целую плоскость, а в прямую.

Собственные значения и собственные векторы

Линейного преобразования

Определение: Пусть L – заданное n- мерное линейное пространство. Ненулевой вектор L называется собственным вектором линейного преобразования А, если существует такое число l, что выполняется равенство:

A .

При этом число l называется собственным значением (характеристическим числом) линейного преобразования А, соответствующего вектору .

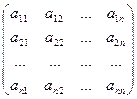Определение: Если линейное преобразование А в некотором базисе , ,…, имеет матрицу А = , то собственные значения линейного преобразования А можно найти как корни l₁, l₂, … ,l_n уравнения:

Это уравнение называется характеристическим уравнением, а его левая часть- характеристическим многочленом линейного преобразования А.

Пример. Найти характеристические числа и собственные векторы линейного преобразования с матрицей А = .

Запишем линейное преобразование в виде:

Составим характеристическое уравнение:

l² - 8l + 7 = 0;

Корни характеристического уравнения: l₁ = 7; l₂ = 1;

Для корня l₁ = 7:

Из системы получается зависимость: x₁ – 2x₂ = 0. Собственные векторы для первого корня характеристического уравнения имеют координаты: (t; 0,5t) где t- параметр.

Для корня l₂ = 1:

Из системы получается зависимость: x₁ + x₂ = 0. Собственные векторы для второго корня характеристического уравнения имеют координаты: (t; -t) где t- параметр.

Полученные собственные векторы можно записать в виде:

Пример. Найти характеристические числа и собственные векторы линейного преобразования А, матрица линейного преобразования А = .

Составим характеристическое уравнение:

(1 - l)((5 - l)(1 - l) - 1) - (1 - l - 3) + 3(1 - 15 + 3l) = 0

(1 - l)(5 - 5l - l + l² - 1) + 2 + l - 42 + 9l = 0

(1 - l)(4 - 6l + l²) + 10l - 40 = 0

4 - 6l + l² - 4l + 6l² - l³ + 10l - 40 = 0

-l³ + 7l² – 36 = 0

-l³ + 9l² - 2l² – 36 = 0

-l²(l + 2) + 9(l² – 4) = 0

(l + 2)(-l² + 9l - 18) = 0

Собственные значения: l₁ = -2; l₂ = 3; l₃ = 6;

1) Для l₁ = -2:

Если принять х₁ = 1, то Þ х₂ = 0; x₃ = -1;

Собственные векторы:

2) Для l₂ = 3:

Если принять х₁ = 1, то Þ х₂ = -1; x₃ = 1;

Собственные векторы:

3) Для l₃ = 6:

Если принять х₁ = 1, то Þ х₂ = 2; x₃ = 1;

Собственные векторы:

Введение в математический анализ

Предел функции в точке

y f(x)

A + e

A

A - e

0 a - D a a + D x

Пусть функция f(x) определена в некоторой окрестности точки х = а (т.е. в самой точке х = а функция может быть и не определена)

Определение. Число А называется пределом функции f(x) при х®а, если для любого e>0 существует такое число D>0, что для всех х таких, что

0 < ïx - aï < D

верно неравенство ïf(x) - Aï< e.

То же определение может быть записано в другом виде:

Если а - D < x < a + D, x ¹ a, то верно неравенство А - e < f(x) < A + e.

Запись предела функции в точке: