Гидростатическое давление и его свойства
Напомним, что в разделе гидростатики исследуется жидкость, находящаяся в состоянии равновесия (или относительного покоя), скорости движения и угловые скорости сдвига равны нулю. В этом случае сопротивляемость жидкости сдвигающим и растягивающим усилиям отсутствует.
Введем понятие гидростатического давления.
Рассмотрим произвольный объем жидкости, находящийся в равновесии (рис. 2.1). Мысленно рассечем его плоскостью BC на две части I и II, первую мысленно отбросим. Для сохранения равновесия второй части суммарное воздействие на нее отсеченной части заменим силой P.

 I ΔP
I ΔP

 B Δω A C
B Δω A C
II
Рис. 2.1
Пусть площадь всей плоскости разреза равна ω. Тогда среднее гидростатическое давление на площади BC
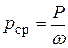 .
.
Для того, чтобы определить давление в точке A, выделим вокруг нее малую площадку Δω, сила, приходящаяся на эту площадку – ΔP.
Гидростатическим давлением в точке A называется предел
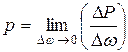 .
.
Из определения текучести среды следует, что в состоянии покоя в жидкости касательные напряжения равны нулю, и в каждой точке произвольно ориентированной в пространстве площадки действуют только нормальные напряжения. Отсюда вытекает первое свойство гидростатического давления: гидростатическое давление всегда совпадает с направлением внутренней нормали к рассматриваемой площадке.
Предположим обратное – что сила гидростатического давления направлена не по нормали к поверхности выделенного объема. Тогда ее можно разложить на нормальную и касательную составляющие. Но касательная составляющая вызвала бы скольжение жидкости вдоль поверхности. А мы рассматриваем случай покоящейся жидкости, т. е. неподвижной и находящейся в равновесии. Значит, на поверхности существуют только нормальные составляющие давления. Более того, они направлены внутрь рассматриваемого объема (иначе на поверхности возникли бы растягивающие напряжения, а их жидкости не воспринимают), следовательно, являются сжимающими.
Второе свойство гидростатического давления состоит в следующем: величина гидростатического давления в данной точке не зависит от направления той площадки, на которую оно действует.
 |  |












 p1
p1
 | |||||
 | |||||
 | |||||


 p2
p2
 |
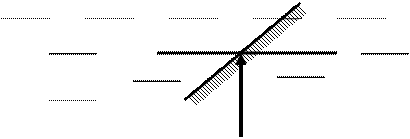
Рис. 2.2
Направление площадки будем характеризовать направлением нормали к ней. Второе свойство давления означает, что если через одну точку внутри жидкости провести две по-разному ориентированные площадки (рис. 2.2), то гидростатические давления p1и p2, действующие на этих площадках, по величине будут одинаковы, т. е. 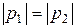 .
.
Для доказательства второго свойства давления выделим в неподвижной жидкой среде элементарный объем в форме тетраэдра (рис. 2.3) с ребрами, параллельными координатным осям и соответственно равными dx, dy, dz.
 | |||
 |
z
 py+εy
py+εy
 |

 dzpn+εn
dzpn+εn
 px+εx
px+εx
dx


 x
x
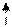 dy
dy
 |
 pz+εz
pz+εz
y
Рис. 2.3
Рассмотрим условия равновесия этого объема жидкости. В общем случае на тетраэдр действуют следующие силы:
· объемные силы, проекции на оси которых, приходящиеся на единицу массы, будут X, Y, Z;
· поверхностные силы со стороны отброшенной части жидкости.
Составим уравнение равновесия в проекции, например, на ось x.
Проекция объемных сил, действующих на весь тетраэдр, будет:
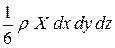 .
.
Обозначим давление в центре координат – p, проекции его – px, py, pz.
Тогда давление в центре тяжести грани dydz можем записать как (px + εx), где εx – малая величина. Аналогично, давление в центре тяжести грани dxdy будет (pz + εz), в центре тяжести грани dxdz – (py + εy), в центре тяжести скошенной грани – (pn + εn). Силы, действующие на грани, получаем, умножая эти давления на площади соответствующих граней.
Поскольку давления на грани dxdy и dxdz перпендикулярны оси x, их проекции на эту ось будут нулевыми и уравнение равновесия в проекции на ось x будет:
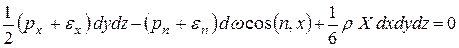 .
.
Здесь dω – площадь скошенной грани тетраэдра, (n,x) – угол между осью x и нормалью к скошенной грани n.
Последним членом уравнения, как бесконечно малой величиной высшего порядка по отношению к другим членам уравнения, можно пренебречь.
Произведение dω cos (n,x) – это проекция скошенной грани на плоскость yz. Тогда
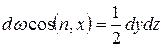 .
.
С учетом этого из уравнения получаем
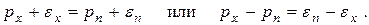
Так как размеры тетраэдра выбраны произвольно, то, уменьшая их (стягивая тетраэдр в точку), будем иметь: 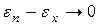 . Из этого следует, что
. Из этого следует, что 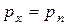 . Рассуждая аналогично для проекций уравнения равновесия на другие оси, в результате получим:
. Рассуждая аналогично для проекций уравнения равновесия на другие оси, в результате получим:
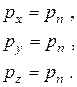
Следовательно,
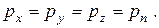
Направление n также выбрано произвольно, следовательно, гидростатическое давление не зависит от наклона площадки, на которую оно действует. При этом давление не будет одинаковым в разных точках пространства, занятого жидкостью, гидростатическое давление в точке зависит от ее координат в пространстве:
p = f (x, y, z).
Законы распределения давления в покоящейся жидкости и рассматриваются в гидростатике.
Заметим, что касательные напряжения в покоящейся жидкости равны нулю независимо от вязкости жидкости, а не только в идеальной жидкости.
Для сохранения сплошности жидкости давление в ней не должно быть меньше некоторого минимума, равного давлению насыщенных паров при данной температуре, т. е.
p > pmin = pн.п.
Если это условие не соблюдается, то при понижении давления ниже минимального происходит разрыв сплошности жидкости. Жидкость закипает, т. е. при понижении давления в жидкости начинается образование пузырьков пара. Если жидкость движется, то возникает явление кавитации.
