Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых

Уравнение прямой в пространстве Параметрические и канонические уравнения прямой

Положение прямой l однозначно определяется точкой M₀ на прямой и вектором 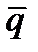,коллинеарным ей. Вектор 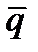называется направляющим вектором прямой.

Пусть 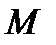-текущая точка на прямой l, т.е. точка, пробегающая всю прямую, и пусть Oxyz - прямоугольная декартова система.

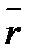M0

z

y

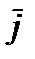M

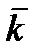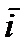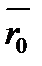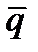Рис. 1

x

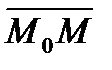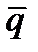Векторы и коллинеарны (рис. 1).

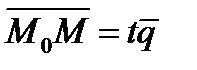,где 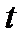-число

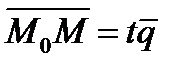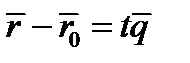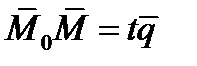, или (1)

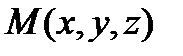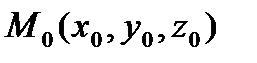Уравнение (1) носит название векторного параметрического уравнения прямой. Скалярные уравнения прямой в пространстве получим с помощью координат векторов и точек. Обозначим координаты точек через и , координаты направляющего вектора обозначим 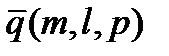. Тогда получим параметрические уравнения прямой:

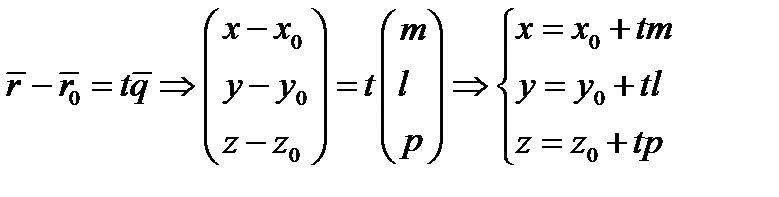(2)

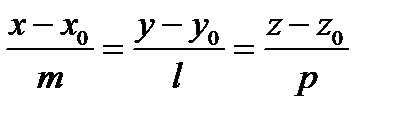(3)

Уравнения (3) называетсяканоническимиуравнениями прямой.

Одну и ту же прямую можно определить разными по форме уравнениями.

Общие уравнения прямой

Прямую в пространстве можно рассматривать как линию пересечения двух плоскостей:

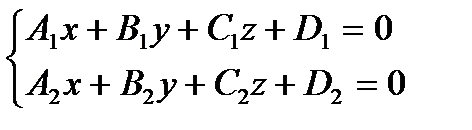(4)

Уравнения (2) умножим на 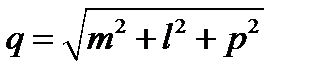и запишем их в таком виде:

,

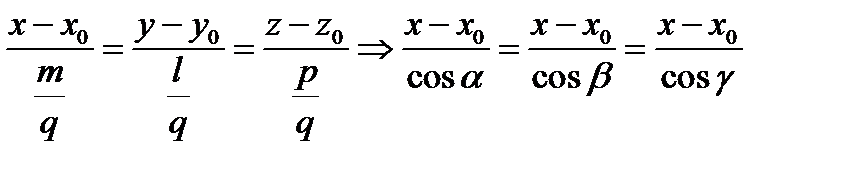где a,b,g - углы, образованные прямой с осями координат Ox, Oy, Oz. Величины cosa, cosb, cosg называются направляющими косинусами прямой и вычисляются с помощью формул:

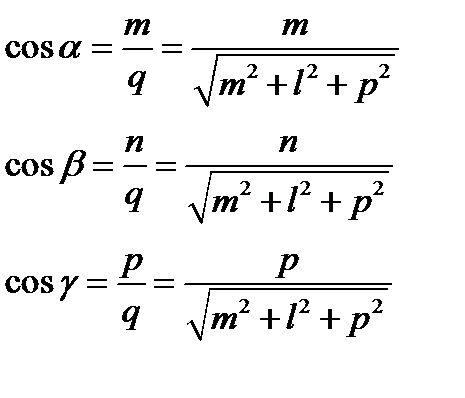(5)

Уравнения прямой, проходящей через две заданные точки

Пусть прямая проходит через две данные точки М₁(x₁,y₁,z₁) и М₂(x₂,y₂,z₂). В этом случае можно считать, что направляющий вектор прямой 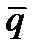= =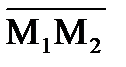(x₂ - x₁, y₂ - y₁, z₂ - z₁).

Подставив в уравнения (3) m = x₂-x₁, l = y₂ - y₁, p = z₂ - z_1, x₀ = x₁, y₀ = y₁, z₀ = z₁, получим .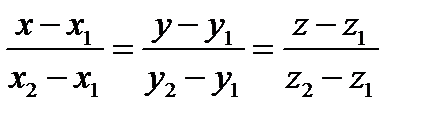

Это уравнение прямой, проходящей через две данные точки.

Замечание.1. Три точки М₁ ,М₂ ,М₃ лежат на одной прямой, если выполняется условие (x₃ - x₁)/(x₂ - x₁) = (y₃ - y₁)/(y₂ - y₁) = (z₃ - z₁)/(z₂ - z₁)

От общих уравнений прямой (4) можно перейти к каноническим уравнениям (3) и наоборот.

Так как предполагается, что плоскости в (4) не параллельны и, тем более, не совпадают, то хотя бы одно из соотношений должно быть выполнено:

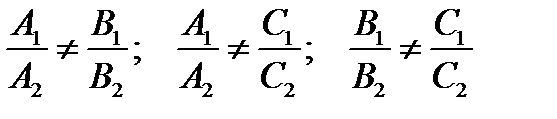. Пусть, например, 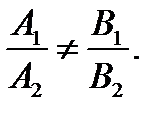Положим 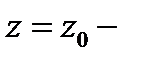любое число.

Тогда получим систему уравнений 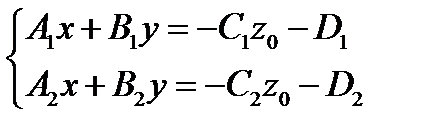, определитель которой не равен нулю.

Пусть 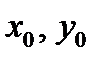-решение этой системы, тогда мы нашли точку на прямой 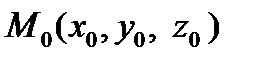. В качестве нормали можем взять вектор 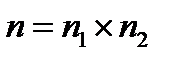, где .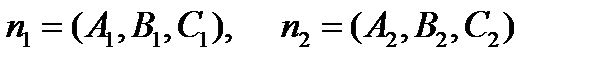

Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых

Пусть даны прямые l₁ и l₂:

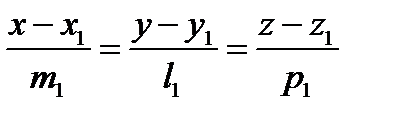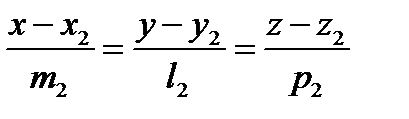и (6)

(7)

Определение. Углом между двумя прямыми l₁ и l₂ называется угол между их направляющими векторами 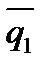(m₁,l₁,p₁) и 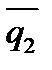(m₂,l₂,p₂) (рис.2).

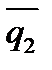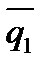j1

l2

l1

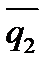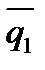j1

l2

l1

Рис.2

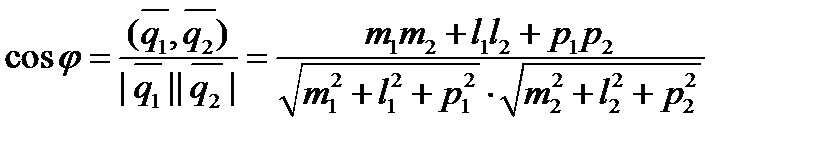(7)

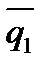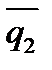Если прямые (6) параллельны, то и коллинеарны. Отсюда получаем условие параллельности прямых:

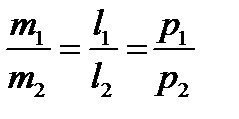(8)

Если прямые (6) взаимно перпендикулярны, то 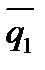и 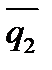также перпендикулярны и их скалярное произведение равно нулю, т.е. (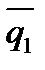 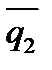) = 0 Þ

m₁m₂ + l₁l₂ + p₁p₂ = 0. Этоусловие перпендикулярностидвух прямых (9)

Угол между прямой и плоскостью.
Условия параллельности и перпендикулярности
прямой и плоскости

Пусть даны прямые: 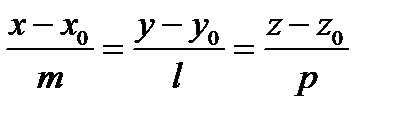(10)

и плоскость Ax + By + Cz + D = 0 (11)

Углом между прямой l и плоскостью pназывается угол j, образованный прямой с её проекцией на плоскость (рис.6.6.)

p

j

p/2-j

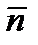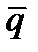l’ - проекция l на плоскость p

Рис. 3.

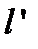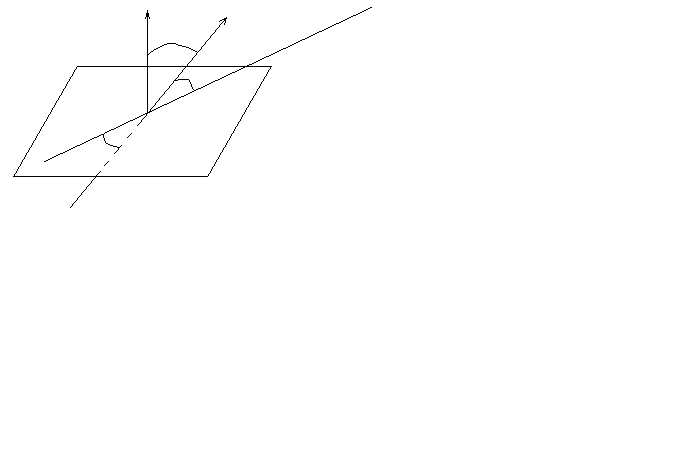
Из рис. 3 видно, что угол между 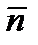(A,B,C) плоскости p и 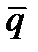(m,l,p) - направляющим вектором прямой равен p/2 - j, поэтому

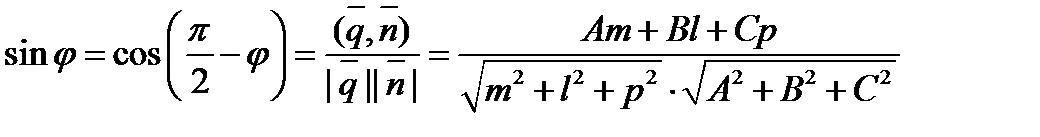(12)

Условие перпендикулярностипрямой (10) и плоскости (11) совпадает с условием коллинеарности векторов 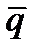и 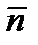, поэтому это условие запишется в виде:

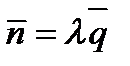или A/m = B/l = C/p (13)

Условие же параллельностипрямой (10) и плоскости (11) совпадает с условием перпендикулярности векторов 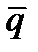и 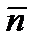; следовательно, получим:

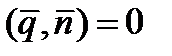или Am + Bl + Cp = 0 (14)