Математические модели аналоговых линий и каналов связи.

При передаче по каналам сигнал претерпевает целый ряд преобразований как преднамеренных, в передатчике и приемнике, так и непреднамеренных, вызванных изменением параметров канальной аппаратуры. Большинство преобразователей - четырехполюсники. Четырехполюсник называется линейным, если оператор, связывающий вход с выходом линейный: .

Основное прикладное свойство линейных операторов состоит в том, что реакция на сумму входных воздействий равна сумме реакций на каждое из воздействий

Именно это свойство дает простой способ анализа прохождения сигнала через цепь. По этой причине, как правило, реальный канал (нелинейный) в первом приближении полагают линейным.

Наиболее общий вид линейного оператора - линейное дифференциальное уравнение. Простейшие примеры:

· Дифференцирование

· Интегрирование

· Интегрирование с заданным весом

Чтобы иметь компактную форму записи преобразования, задаваемого дифференциальным уравнением (*), вводят обозначение для дифференцирования.

Тогда

и , где y - выход, x- вход,

Наиболее простой вариант для анализа, когда a(p,t) и b(p,t) - от t не зависят.

Имеем первый вариант задания такой линейной цепи и известный способ анализа прохождения сигнала по каналу. Надо решить линейное дифференциальное уравнение с постоянными коэффициентами:

,

где первая часть есть общее решение однородного уравнения, а вторая часть B(t) – частное решение неоднородного, p_n – корни характеристического уравнения .

Интерес представляют устойчивые четырехполюсники, для них вещественные части корней отрицательны, корни различны. Если 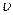_вх(t) имеет преобразование Фурье, начальные условия нулевые, то можно использовать операционное исчисление для решения дифференциального уравнения.

Возьмем преобразование Фурье от правой и левой частей уравнения (*)

.

Обозначим , это комплексный коэффициент передачи канала

Можно использовать показательную форму , где

- АЧХ канала

- ФЧХ канала

или

Приходим к заключению, что четырехполюсник задается своим комплексным коэффициентом передачи k(w).

Зная входной сигнал, легко вычисляется выходной:

1. находим спектр входного сигнала (по таблице прямого преобразования Фурье)

2. вычисляем спектр выходного, как произведение k(w) и входного спектра

3. находим выходной сигнал, как функцию времени (по таблицам обратного преобразования Фурье)

Обсудим, что представляет собой АЧХ и ФЧХ «физически».

Утверждается, что только гармонический сигнал остается таковым же при прохождении через линейный фильтр. Изменится лишь амплитуда и фаза. АЧХ - это «коэффициент» усиления гармоник, ФЧХ - отражает задержку гармоник.

Метод анализа становится стандартным: переход от временного представления сигнала к спектральному ® нахождение спектра выходного сигнала ® обратный переход к временному представлению сигнала.

Линейный четырехполюсник может быть задан и еще одним способом - заданием импульсной переходной функции

Импульсная переходная функция, есть не что иное, как реакция четырехполюсника на входное воздействие в виде 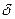- функции (единичную энергию, сосредоточенную в очень малом промежутке времени).

Выходной сигнал через h(t) находится как:

т.к. h(t)=0, t<0 при , t<0

Принцип причинности и выбор начала отсчета дает возможность далее всегда писать:

Каков должен быть комплексный коэффициент передачи канала, чтобы любой сигнал проходил по нему без искажения?

Для неискаженной передачи сигнала необходимо, чтобы отклик линейной системы был точной копией входного сигнала. Допускается различие только в амплитуде, так как важна форма, а не величина отклика. Кроме того, выходной сигнал может запаздывать по времени относительно входного сигнала. Отсюда очевидно, что коэффициент передачи системы должен быть постоянным на всех частотах, а фазовый сдвиг удовлетворять определенному соотношению.

Действительно, если сигнал передается без искажения, то

.

По теореме запаздывания (свойство 4 преобразования Фурье) мы можем утверждать, что

.

Следовательно, неискажающая система должна иметь коэффициент передачи

.

Изобразим эту функцию в виде двух характеристик: амплитудно-частотной и фазочастотной.

Для неискаженной передачи сигналов необходимо, чтобы амплитудно-частотная характеристика была постоянна на всех частотах, а фазочастотная – линейна. Коэффициент линейности в силу принципа причинности должен быть отрицательным и иметь размерность времени.

Тот факт, что фазовый сдвиг оказался пропорциональным частоте означает просто постоянную задержку на всех частотных составляющих. Поскольку добавление фазового сдвига может привести лишь к изменению знака сигнала, более строго можно записать

Степень постоянства величины реальной системы обычно характеризуют ее полосой пропускания. Полоса пропускания – это интервал частот, в пределах которого не становится меньше своего значения на средней частоте.

=( ) – полоса пропускания.

Реальную систему с бесконечной полосой пропускания из-за физических ограничений сделать невозможно. Удовлетворительную неискаженную передачу можно обеспечить при достаточно большой, но конечной полосе пропускания. Это связано с тем, что энергия реальных сигналов убывает с увеличением частоты. Ослабление высокочастотных составляющих в этом случае приведет к незначительным искажениям сигнала, поскольку частотные составляющие, содержащие наибольшую часть энергии сигнала, передается без ослабления.

Часто используются для задания реальных фильтров модели идеальных фильтров: идеальный фильтр нижних частот, идеальный фильтр верхних частот, идеальный полосовой фильтр. АЧХ и ФЧХ таких фильтров приведены ниже.

Искажения сигналов, вызванные ограниченностью АЧХ