Статистические методы распознавания. Метод Бейеса.

Основное преимущество статических методов распознавания состоит в возможности одновременного учета признаков различной физической природы, т.к. они характеризуются безразмерными величинами - вероятностями их появления при различных состояниях системы.

Метод Байесса.

Среди методов ТД, метод основанный на обобщенной формуле Б. который занимает особое место благодаря простоте и эффективности.

Основные недостатки: большой объем предварительной информации, угнетение редко встречающихся диагнозов и др.

Основы метода.

Метод основан на простой формуле Байесса. Если имеется диагноз 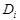и простой признак 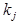, встречающийся при этом диагнозе, то вероятность совместного появления событий:

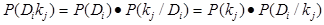. (1)

Из этого равенства формула Байесса:

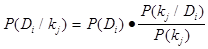, (2)

где 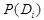- вероятность диагноза 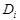, определяемая по статистическим данным (априорная вероятность диагноза). Так если предварительно обследовано 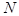объектов и у 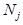имелось состояние 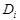, то

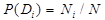. (3)

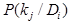-вероятность появления признака у объектов с состоянием 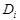. Если среди 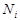объектов, имеющих диагноз 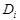, у 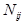появился признак 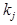, то

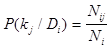. (4)

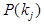-вероятность появления признака 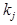во всех объектах независимо от состояния объекта. Пусть из общего числа 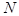объектов признак 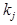был обнаружен у 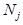объектов, тогда:

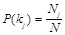. (5)

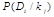-вероятность диагноза 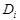после того как стало известно наличие у рассматриваемого объекта признак .

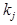Обобщенная формула Байесса.

Эта формула относится к случаю когда обследование проводится по комплексу признаков 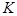, включающему признаки 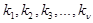. Каждый из признаков 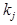имеет 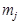разрядов 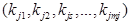. В результате обследования становится известной реализация признака

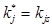, (6)

и всего комплекса 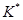(*-означает конкретное значение признака).

Формула Байесса для комплекса признаков:

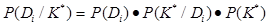, (7)

где 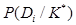-вероятность диагноза 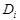, после того как стали известны результаты обследования по комплексу признаков .

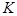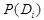-предварительная вероятность диагноза 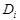(по предшествующей статистике). Здесь предполагается, что система находится только в одном из состояний и

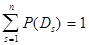. (8)

Если комплекс признаков состоит из 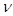признаков, то

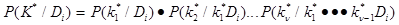. (9)

Для диагностически независимых признаков:

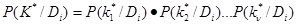. (10)

Вероятность появления комплекса признаков :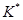

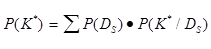. (11)

Обобщенная формула Байесса может быть записана в виде:

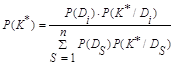(12)

где 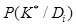определяется по (9) или (10). Из соотношения вытекает:

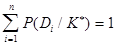. (13)

Следует отметить, что знаменатель формулы Байесса одинаков для всех диагнозов. Это позволяет определить сначала вероятность совместного появления i-го диапазона и данной реализации:

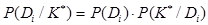, (14)

и затем апостериорную вероятность диагноза:

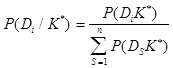. (15)

Если реализация некоторого комплекса признаков 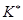является детерминирующей для диагноза 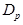, то этот комплекс не встречается при других диагнозах:

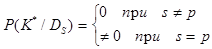
Тогда

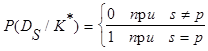(15)

Для определения вероятности диагнозов по методу Байесса необходимо составить диагностическую матрицу, которая формируется на основе предварительного статистического материала:

Диагноз	Признак kj
Di	k1	k2	k3	P(Di)
	P(k11/Dj)	P(k12/Dj)	P(k13/Dj)	P(k21/Dj)	P(k22/Dj)	P(k23/Dj)	P(k24/Dj)	P(k31/Dj)	P(k32/Dj)
D1	0,8	0,2		0,1	0,1	0,6	0,2	0,2	0,8	0,3
D2	0,1	0,7	0,2			0,3	0,7	0,1	0,9	0,1
…

В диагностическую матрицу включены априорные вероятности диагнозов. Процесс обучения в методе Байесса состоит в формировании диагностической матрицы. Важно предусмотреть возможность уточнения таблицы в процессе диагностики. Для этого в памяти ЭВМ следует хранить не только значения 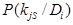, но и следующие величины: 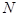-общее число объектов, использованных при составлении матрицы; 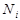-число объектов с диагнозом 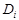; 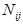-число объектов с диагнозом 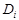, обследованных по признаку 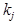. Если поступает новый объект с диагнозом 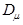, то производится корректировка прежних априорных вероятностей диагнозов:

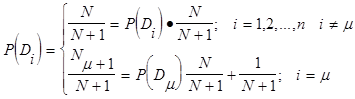(17)

Далее вводятся поправка к вероятностням признаков

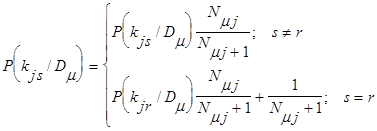, (18)

где 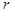- разряд признака .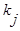

Пример 1.

Пусть при наблюдении за газотурбинным двигателем проверяются два признака: 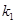-повышение температуры газа за турбиной более чем на 50⁰ С и

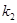- увеличение времени выхода на максимальную частоту вращения более чем на

5 с. Предположим, что для данного типа двигателей появление этих признаков связано либо с неисправностью топливного регулятора(состояние 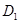), либо с увеличение радиального зазора в турбине(состояние ).

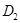При нормальном состоянии двигателя (состояние 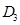) признак 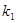не наблюдается, а признак 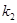наблюдается в 5% случаев. На основании статистических данных известно, что 80% двигателей вырабатывают ресурс в нормальном состоянии, 5% двигателей имеют состояние 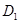и 15% - состояние 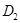. Известно также, что признак 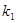встречается при состоянии 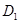в 20%. а при состоянии 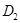в 40%случаев; признак 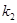при состоянии 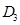встречается в 30%, а при состоянии 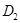-в 50% случаев. Сведем эти данные в диагностическую таблицу(таблица 2).

Найдем сначала вероятности состояний двигателя, когда обнаружены оба признака 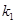и 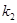. Для этого, считая признаки независимыми, применим формулу (12).

Вероятность состояния

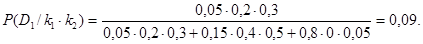
Аналогично получим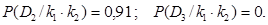

Определим вероятность состояний двигателя, если обследование показало, что повышение температуры не наблюдается(признак 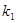отсутствует), но увеличивается время выхода на максимальную частоту вращения(признак 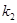наблюдается). Отсутствие признака 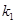есть признак наличия 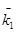, причем 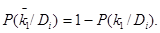Для расчета применяют также формулу (12), но значение 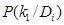в диагностической таблице заменяют на 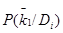. В этом случае

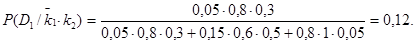
и аналогично 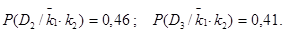Вычислим вероятности состояний в том случае, когда оба признака отсутствуют. Аналогично предыдущему получим

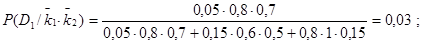
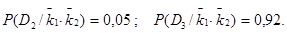
Отметим. что вероятности состояни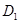й и 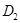отличны от нуля, так как рассматриваемые признаки не являются для них детерминирующими. Из проведенных расчетов можно установить, что при наличии признаков 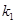и 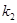в двигателе с вероятностью 0,91 имеется состояние 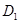, т.е. увеличение радиального зазора. При отсутствии обоих наиболее вероятно нормальное состояние(вероятность 0,92). При отсутствии признака 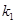и наличии признака 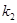вероятности состояни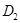й и 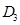примерно одинаковы(0,46 и 0,41) и для уточнения состояния двигателя требуется проведение дополнительных обследований.

Таблица 2.

Вероятности признаков и априорные вероятности состояний.

Di	P(k1/Di)	P(k2/Di)	P(Di)
D1 D2 D3	0,2 0,4 0,0	0,3 0,5 0,05	0,05 0,15 0,80

Решающее правило.

Правило, в соответствии с которым принимается решение о диагнозе. В методе Байесса объект с комплексом признаков 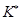относится к диагнозу с наибольшей(апостериорной) вероятностью:

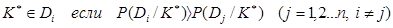. (19)

Пороговое значение для вероятности диагноза: 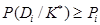, (20)

где 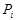-заранее выбранный уровень распознавания для диагноза .

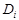При: 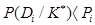(21)

- решение о диагнозе не принимается (отказ от распознавания) и требует поступления новой информации.

При практических расчетах целесообразно провести диагностику и для случая равновероятностных диагнозов, положив

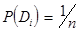. (22)

Тогда наибольшим значением апостериорной вероятности будет обладать 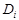, для которого 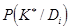максимальна.

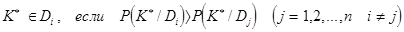(23)

Такое решающее правило соответствует методу максимального правдоподобия.

Пороговое значение для (23):

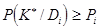(24)