Задача 2. Расчёт статически определимого ступенчатого бруса при растяжение (сжатие)

Для статически определимого ступенчатого бруса с жёстко защемлённым концом (см. схемы к задаче 2), нагруженного продольными усилиями Р₁ ,Р₂ , q₁ и q₂ (см. таб. 1.2), необходимо:

1. Построить эпюры продольных сил N, нормальных напряжений s и перемещений .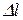

2. Подобрать величину площади поперечных сечений для всех участков бруса из условия прочности по допускаемым нормальным напряжениям при растяжении и сжатии.

Таблица 1.2

№	Р1, кН	Р2, кН	q1, кН/м	q2, кН/м
	10	80	10	70
	20	70	15	80
	30	60	20	90
	40	50	25	60
	50	40	30	50
	60	30	35	40
	70	10	40	30
	80	20	45	20
	10	50	55	50
	20	70	65	20

Принять для всех вариантов следующие соотношения: 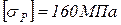, , 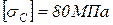Е=10⁵МПа, а=1м.

Схемы к задаче 2

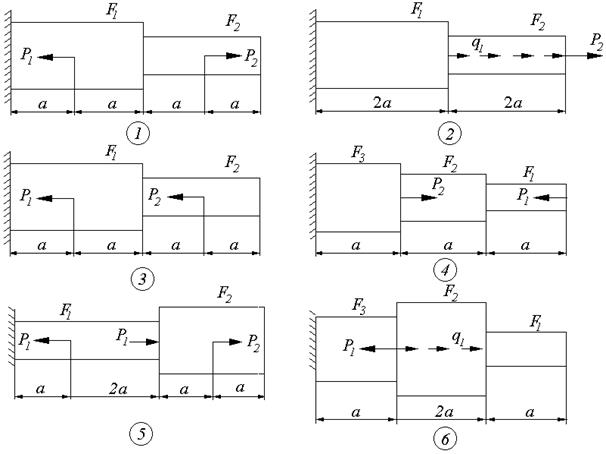
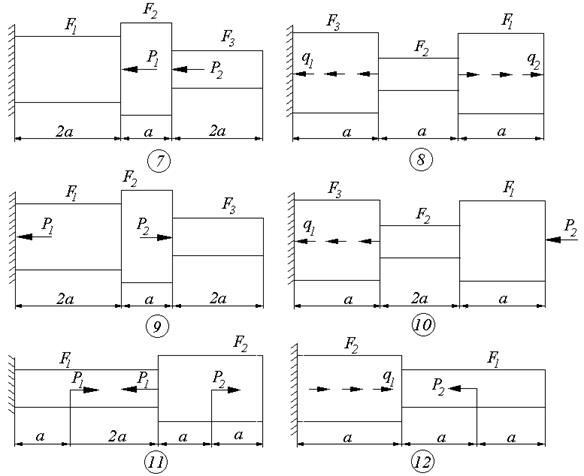
Схемы к задаче 2

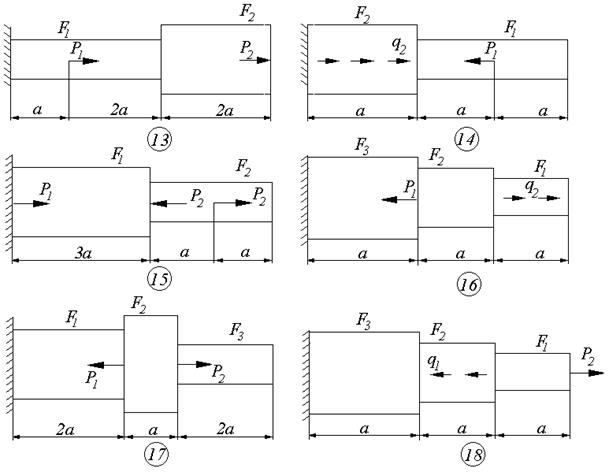
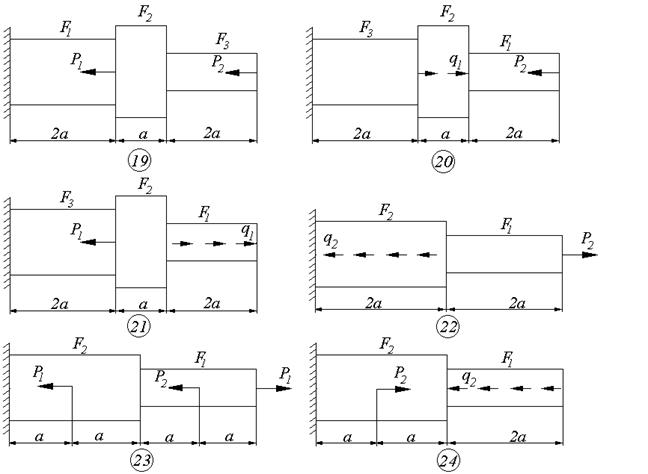
Схемы к задаче 2

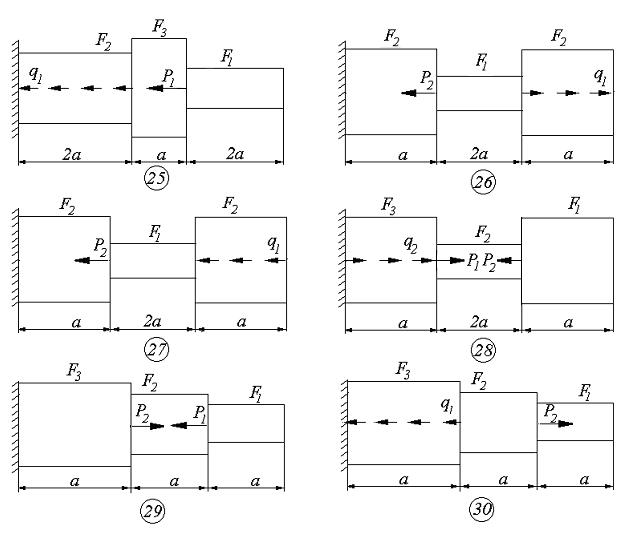
Пример решения задачи 2

Для ступенчатого бруса (см. рис.1.4,а) с жёстко защемлённым концом необходимо:

1. Построить эпюры продольных сил N, нормальных напряжений s и перемещений .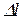

2. Подобрать величину площади поперечных сечений всех участков бруса из условия прочности по нормальным напряжениям, используя следующие числовые значения:

Р₁=30кН; Р₂=20кН; q₂=20кН/м; а=1м; 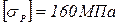; ; 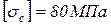Е=1,8×10⁵МПа; F₁=F; F₂=2F; F₃=3F.

Решение

1. Брус состоит из трёх участков. Границами участков являются сечения, к которым приложены внешние силы, или сечения, где изменяются размеры поперечных сечений.

Величину внутренних продольных усилий определим, используя метод сечений. При этом рассматриваем всё время правую отсечённую часть бруса.

Продольную силу N считаем положительной, если нагрузка, её создающая, вызывает растяжение рассматриваемого участка, т.е. направлена от рассматриваемого сечения. Нагрузка, вызывающая сжатие рассматриваемой части бруса, т.е. направленная к сечению, создаёт отрицательную продольную силу. В соответствии с расчётной схемой (рис. 1.4) аналитические зависимости для внутреннего продольного усилия N будут иметь следующий вид:

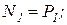
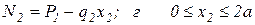
тогда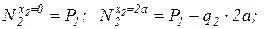

.

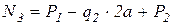После подстановки численных значений, получим:

.

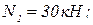
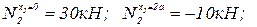
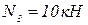На основании полученных значений строим эпюру продольных сил N.

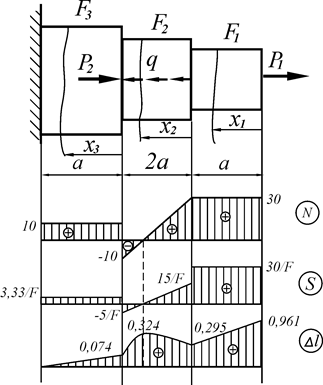
Рис. 1.4 Схема нагружения и эпюры N, σ и Δl для ступенчатого

статически определимого бруса

2. Эпюру нормальных напряжений s получим, разделив значения продольной силы N на соответствующие площади поперечных сечений бруса. Знак продольной силы N определяет и знак соответствующего нормального напряжения s.

,

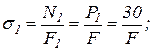
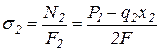подставляя 2 крайних значения х₂ будем иметь:

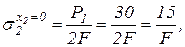
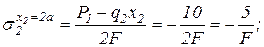
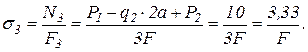
3. Из условия прочности по нормальным наибольшим напряжениям растяжения и сжатия определим параметр F, а затем площади поперечных сечений каждого участка бруса.

Из условия прочности по растягивающим нормальным напряжениям находим:

,

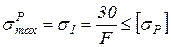отсюда .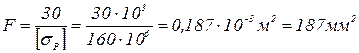

Из условия прочности по сжимающим нормальным напряжениям находим:

,

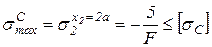тогда .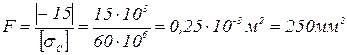

Из двух полученных значений выбираем наибольшее значение параметра F=250мм².

Определим площади поперечных сечений каждого участка:

F₁=F=250мм², F₂=2F=500мм², F₃=3F=750мм².

3. Зная площади поперечных сечений можно построить эпюру перемещений 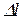. Проще расчёт перемещений вести от заделки, т.е. за точку отсчёта брать сечение, перемещение которого равно 0.

.

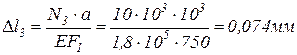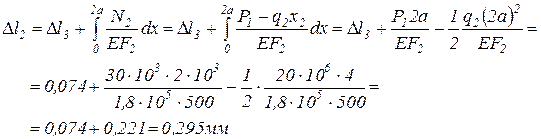
Т.к. уравнение для перемещения на втором участке содержит квадратичную функцию, то графиком функции перемещения на втором участке будет являться парабола, причём в сечении, где 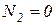парабола будет иметь экстремум. Приравняв уравнение для продольной силы 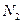к 0, получим расстояние х₀ до этого сечения.

,

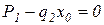где 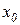- расстояние до сечения, в котором .

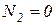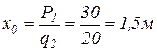
Подставляя, полученное значение для 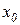, получим значение экстремума на параболе:

.

.

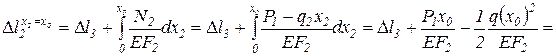
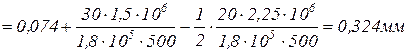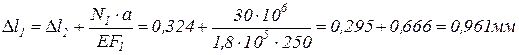По найденным значениям 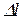строим эпюру перемещений.