Функции нескольких переменных. Основные понятия
Основные понятия
1.1. Для определения функции нескольких переменных необходимы некоторые понятия, связанные с геометрией на плоскости и в пространстве.
Точки на плоскости 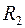 обозначаются
обозначаются 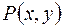 или просто
или просто 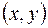 , где x и y называются координатами точки P. Расстояние между точками
, где x и y называются координатами точки P. Расстояние между точками 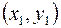 и
и 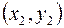 определяется формулой
определяется формулой
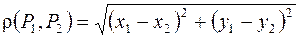 .
.
Для удобства перехода к n-мерному пространству 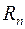 точки на плоскости
точки на плоскости 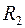 можно обозначить
можно обозначить 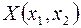 , где x1 и x2 будут называться координатами точки X, а расстояние между точками
, где x1 и x2 будут называться координатами точки X, а расстояние между точками 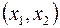 и
и 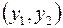 будет определяться формулой
будет определяться формулой
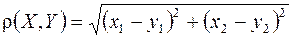 .
.
В n-мерном евклидовом пространстве 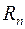 расстояние между точками
расстояние между точками 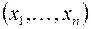 и
и 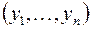 вычисляется аналогично:
вычисляется аналогично:
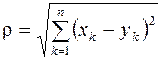 .
.
Принадлежность точки пространству или плоскости обозначается 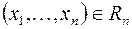 .
.
1.2. Множество точек 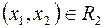 , координаты которых удовлетворяют неравенству
, координаты которых удовлетворяют неравенству
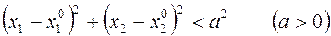 ,
,
называется открытым кругом радиуса a с центром в точке 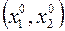 .
.
Множество же точек 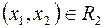 , координаты которых удовлетворяют неравенствам
, координаты которых удовлетворяют неравенствам
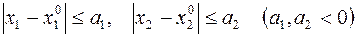 ,
,
называется открытым прямоугольником.
1.3. Любой открытый круг радиуса 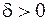 или открытый квадрат со стороной длины
или открытый квадрат со стороной длины 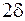 с центром в точке
с центром в точке 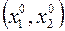 называется δ-окрестностью этой точки.
называется δ-окрестностью этой точки.
Окрестностью точки “ 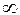 ” ( обозначается
” ( обозначается 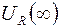 ) называется множество всех точек
) называется множество всех точек 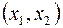 таких, что
таких, что
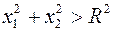 .
.
Это обозначается так: 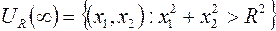 .
.
1.4. Аналогично, множество точек 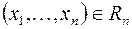 , для которых выполняется неравенство
, для которых выполняется неравенство
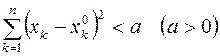 ,
,
называется n-мерным открытым шаром радиуса a с центром в точке 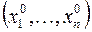 .
.
Множество же точек 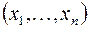 , координаты которых удовлетворяют неравенствам
, координаты которых удовлетворяют неравенствам
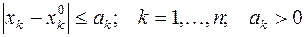 .
.
называется n-мерным открытым параллелепипедом.
1.5. Любой открытый n-мерный шар радиуса δ или куб с центром в точке 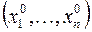 и длиной ребра 2δ называется n-мерной δ-окрестностью этой точки.
и длиной ребра 2δ называется n-мерной δ-окрестностью этой точки.
1.6. Мы рассматривали открытые шары и кубы, но это же верно и для замкнутых шаров и кубов. Только все неравенства, с помощью которых они определялись, будут нестрогими. При этом шары и кубы также являются множествами.
Пусть D- некоторое множество точек пространства 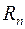 . Точка
. Точка 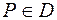 называется внутренней точкой множества D, если существует δ-окрестность
называется внутренней точкой множества D, если существует δ-окрестность 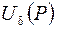 точки P такая, что она полностью включается в множество D
точки P такая, что она полностью включается в множество D
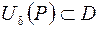 .
.
Точка P называется граничной точкой множества D, если в любой ее δ-окрестности содержатся как точки из множества D, так и точки, не принадлежащие множеству D. Совокупность граничных точек называется границей и обозначается 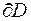 или
или 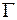 , т.е.
, т.е. 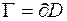 .
.
Множество D называется замкнутым, если 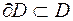 , т.е. любая граничная точка включается в множество D.
, т.е. любая граничная точка включается в множество D.
Множество D называется открытым, если все его точки внутренние.
Множество D называется связным, если любые его две точки можно соединить непрерывной кривой, принадлежащей D.
Связное открытое множество называется областью.
Множество D называется ограниченным, если существует такая δ-окрестность начала координат  , что все точки множества D принадлежат ей.
, что все точки множества D принадлежат ей.
Функции нескольких переменных
2.1. Функция от двух переменных определяется следующим образом. Рассматривается некоторое множество точек  из плоскости
из плоскости 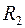 , и если каждой точке
, и если каждой точке 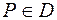 , имеющей координаты
, имеющей координаты 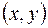 , в силу некоторого закона
, в силу некоторого закона 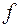 приведено в соответствии число
приведено в соответствии число 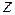 , то говорят, что на множестве
, то говорят, что на множестве  задана функция двух переменных
задана функция двух переменных 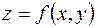 . Множество
. Множество  называется областью определения функции
называется областью определения функции 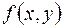 .
.
Функцию 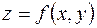 от двух переменных можно изобразить в трехмерном пространстве, где задана прямоугольная система координат
от двух переменных можно изобразить в трехмерном пространстве, где задана прямоугольная система координат 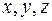 в виде геометрического места точек
в виде геометрического места точек 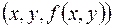 , а область определения – на плоскости
, а область определения – на плоскости 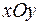 .
.
Пример. Геометрическим местом точек для функции 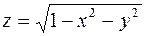 является верхняя половина шаровой поверхности (рис.1). Область определения находится, исходя из условия неотрицательности подкоренного выражения (рис.2):
является верхняя половина шаровой поверхности (рис.1). Область определения находится, исходя из условия неотрицательности подкоренного выражения (рис.2):
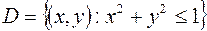
(если граница области не включается, то изображается штриховой линией).
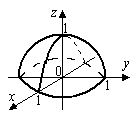 Рисунок 1 Рисунок 1 | 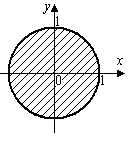 Рисунок 2 Рисунок 2 |
2.2. Не всегда удается изобразить график функции. Построение графиков упрощается с помощью линий уровня.
Линией уровня называется множество точек 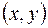 , в которых функция
, в которых функция 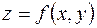 принимает одинаковое значения.
принимает одинаковое значения.
Пример. Построить линии уровня функции 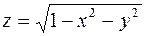 .
.
Согласно определению линии уровня: 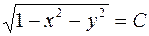 при при 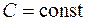 , откуда , откуда 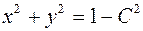 . Это уравнение определяет окружности радиуса . Это уравнение определяет окружности радиуса 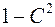 с центром в начале координат (рис.3). При с центром в начале координат (рис.3). При 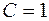 линия уровня выражается в точку линия уровня выражается в точку 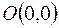 . . 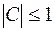 . . | 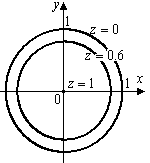 Рисунок 3 Рисунок 3 |
2.3. Функция нескольких переменных, которую можно записать в виде
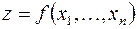 ,
,
определяется аналогично.
При 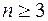 это определение лишено наглядности изображения. При
это определение лишено наглядности изображения. При 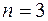 область определения функции можно представить в пространстве. В этом случае вместо линий уровня вводится понятие поверхностей уровня. Они точно так же могут вырождаться в какую-либо кривую или точку.
область определения функции можно представить в пространстве. В этом случае вместо линий уровня вводится понятие поверхностей уровня. Они точно так же могут вырождаться в какую-либо кривую или точку.
Предел функции
3.1. Пусть функция 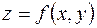 определена в некоторой
определена в некоторой  -окрестности точки
-окрестности точки 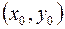 за исключением, быть может, самой этой точки.
за исключением, быть может, самой этой точки.
Число  называется пределом функции
называется пределом функции 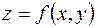 при стремлении точки
при стремлении точки 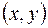 к точке
к точке 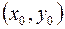 , если для любого
, если для любого 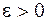 существует такое
существует такое 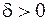 , что из условия
, что из условия
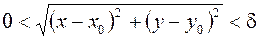
следует
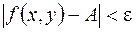 .
.
Предел функции обозначается так:
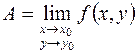 .
.
Пример. Покажем на основе этого определения, что предел функции 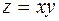 в точке
в точке 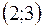 равен 6. Это значит, что для произвольного
равен 6. Это значит, что для произвольного 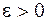 необходимо найти такую точку
необходимо найти такую точку  - окрестности точки
- окрестности точки 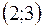 , что из условия
, что из условия 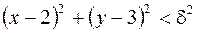 следует равенство
следует равенство 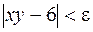 .
.
Рассмотрим квадрат со стороной 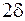 с центром в точке
с центром в точке 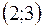 . Если точка
. Если точка 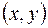 принадлежит этому квадрату, то
принадлежит этому квадрату, то

и для таких точек квадрата
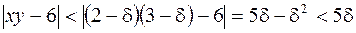
для  . Если положить, что
. Если положить, что 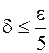 , то получается необходимое неравенство для всех точек квадрата. А для точек круга радиуса
, то получается необходимое неравенство для всех точек квадрата. А для точек круга радиуса  с центром в точке
с центром в точке  тем более выполняется это неравенство. Таким образом, указана
тем более выполняется это неравенство. Таким образом, указана  - окрестность
- окрестность  , для всех точек которой выполняется это неравенство
, для всех точек которой выполняется это неравенство 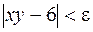 .
.
Пример. Докажем, что функция
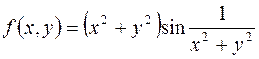
имеет предел, равный нулю, в начале координат 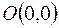 .
.
Функция не определена в точке 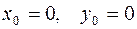 , но имеет предел в этой точке.
, но имеет предел в этой точке.
Зададим произвольное 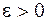 . Тогда если
. Тогда если 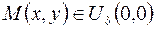 , то по определению
, то по определению  .
.
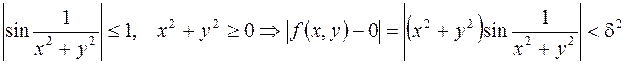 .
.
Положив 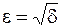 , получаем необходимое неравенство.
, получаем необходимое неравенство.
Пример. Вычислим 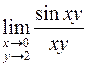 , используя замечательный предел.
, используя замечательный предел.
Функция не определена на оси абсцисс, но в точке 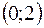 имеет предел. В самом деле, сделав замену
имеет предел. В самом деле, сделав замену 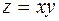 , имеем
, имеем
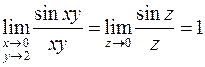 .
.
Пример. Рассмотрим функцию 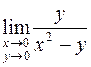 . Пусть точка
. Пусть точка 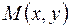 стремится к
стремится к 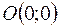 по параболе
по параболе 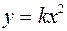 , где
, где 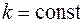 . Тогда
. Тогда
 ,
,
т.е. подходя к точке 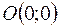 по различным параболам
по различным параболам 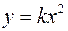 (для различных
(для различных 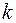 ), получаем различные пределы. А это означает отсутствие предела.
), получаем различные пределы. А это означает отсутствие предела.
3.2. Пусть функция 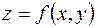 определена в окрестности
определена в окрестности 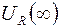 . Число
. Число  называется пределом функции
называется пределом функции 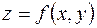 при
при 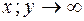 , если для любого
, если для любого 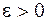 существует такое
существует такое 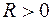 , что из условия
, что из условия
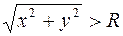
следует, что 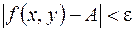 .
.
Пример. Покажем, что
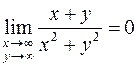 .
.
Зададимся  произвольными
произвольными  . Если
. Если  , то
, то 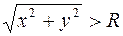 или
или 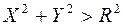 и
и 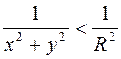 ; далее, очевидно, что
; далее, очевидно, что 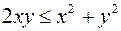 или
или 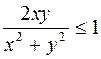 , поэтому
, поэтому 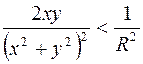 , следовательно
, следовательно 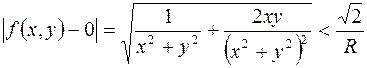 . Положив
. Положив 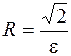 , получим необходимые неравенства.
, получим необходимые неравенства.
Пример. Вычислим 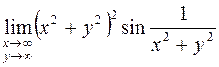 . Для этого введем полярные координаты
. Для этого введем полярные координаты 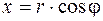 ,
, 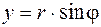 , тогда
, тогда 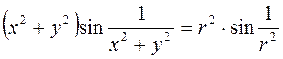 . Из условия
. Из условия 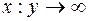 , вытекает, что
, вытекает, что 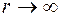 и
и 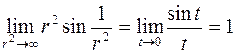 . Здесь произвели замену переменной
. Здесь произвели замену переменной 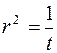 , откуда если
, откуда если 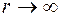 , то
, то 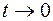 .
.
Непрерывность функции
4.1. Пусть функция 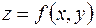 определена в некоторой δ – окрестности точки
определена в некоторой δ – окрестности точки 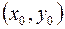 , в том числе в самой точке
, в том числе в самой точке 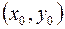 . Функция
. Функция 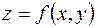 называется непрерывной в точке
называется непрерывной в точке 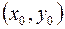 , если предел функции
, если предел функции 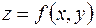 в точке
в точке 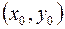 существует и равен значению функции в этой точке, т.е.
существует и равен значению функции в этой точке, т.е. 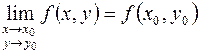 .
.
Функцию 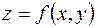 называют непрерывной на множестве D, если она непрерывна в каждой точке этого множества.
называют непрерывной на множестве D, если она непрерывна в каждой точке этого множества.
Условие непрерывности 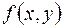 в точке
в точке 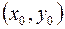 можно записать в эквивалентной форме:
можно записать в эквивалентной форме:
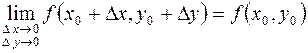 .
.
Можно ввести приращение 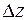 функции
функции 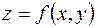 :
:
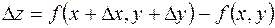 .
.
Это означает, что условие непрерывности функции в точке 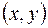 эквивалентно выполнению равенства
эквивалентно выполнению равенства
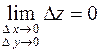 .
.
Понятие предела и непрерывности для функции нескольких переменных аналогичны соответствующим понятиям для функции одной переменной, поэтому основные теоремы для непрерывных функций одной переменной остаются справедливыми и для функции нескольких переменных, при этом роль отрезка играет замкнутое множество.
4.2. Точка множества, в которой функция не является непрерывной, называется точкой разрыва функции. Точки разрыва могут быть изолированными, образовывать линии разрыва, поверхности разрыва ( для 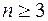 ) и т.д.
) и т.д.
Пример. Функция 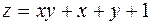 непрерывна при любых значениях x и y, т.е. в любой точке плоскости
непрерывна при любых значениях x и y, т.е. в любой точке плоскости 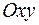 . Действительно, преобразовав функцию
. Действительно, преобразовав функцию
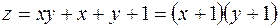 ,
,
найдем приращение функции

следовательно,
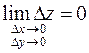 .
.
Пример. Найти точки разрыва функции
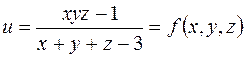 .
.
Функция определена в точках, в которых знаменатель обращается в ноль. Поэтому она имеет поверхность разрыва- плоскость 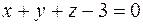 .
.
Заметим, что разрыв в точке 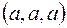 , где
, где 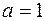 , можно устранить, положив
, можно устранить, положив
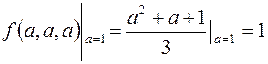 ,
,
т.е. точка 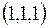 является точкой устранимого разрыва.
является точкой устранимого разрыва.
Пример. Найти точки разрыва функции
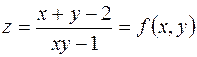 .
.
Заметим, что разрыв в точке 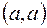 , где
, где 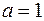 можно устранить, положив
можно устранить, положив
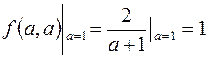 ,
,
т.е. точка 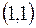 - точа устранимого разрыва.
- точа устранимого разрыва.
Пример. Найти точки разрыва функции
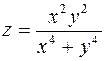 .
.
Функция определена всюду, кроме точки 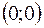 . Рассмотрим значение z вдоль прямой
. Рассмотрим значение z вдоль прямой 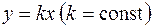 :
:
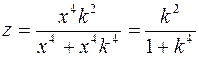 .
.
Подходя к точке 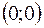 по различным прямым, мы будем получать различные предельные значения, зависящие от k. Это значит, что функция не имеет предела в точке
по различным прямым, мы будем получать различные предельные значения, зависящие от k. Это значит, что функция не имеет предела в точке  . Функцию нельзя доопределить в этой точке так, чтобы она стала непрерывной. Следовательно, эта точка является точкой неустранимого разрыва.
. Функцию нельзя доопределить в этой точке так, чтобы она стала непрерывной. Следовательно, эта точка является точкой неустранимого разрыва.
Частные производные
5.1. Пусть функция 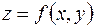 определена в некоторой
определена в некоторой 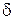 – окрестности точки
– окрестности точки 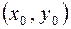 . Если дать независимой переменной
. Если дать независимой переменной 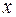 приращение
приращение 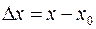 , то функция
, то функция 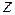 получит приращение, которое называют частным приращением функции
получит приращение, которое называют частным приращением функции 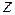 по аргументу
по аргументу 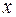 и обозначают символом
и обозначают символом 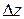 , так что
, так что
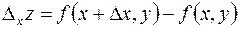 .
.
Аналогично определяется частное приращение 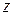 по
по 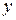 :
:
 .
.
Наконец, сообщив аргументу 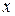 приращение
приращение 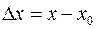 , а аргументу
, а аргументу 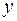 – приращение
– приращение 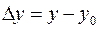 , можно получить для
, можно получить для 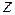 новое приращение
новое приращение 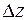 , которое называется полным приращением функции
, которое называется полным приращением функции 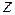 , определяемое формулой
, определяемое формулой
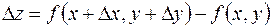 .
.
Надо заметить, что, вообще говоря, полное приращение не равно сумме частных приращений, т.е.
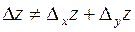 .
.
Пример. 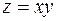 .
.
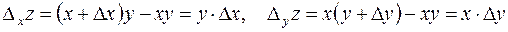

Аналогичным образом определяются частные и полное приращения функции любого числа переменных.
5.2. Частной производной по 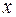 (по
(по 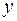 ) от функции
) от функции 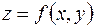 называется предел отношения частного приращения
называется предел отношения частного приращения 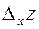 по
по 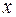 (
( 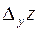 по
по 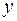 ) к приращению
) к приращению 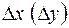 при стремлении
при стремлении 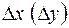 к нулю и обозначается одним из символов
к нулю и обозначается одним из символов
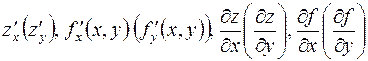 .
.
Таким образом, по определению,
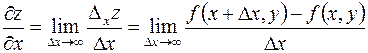 .
.
или
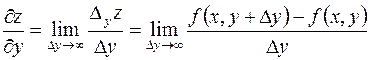 .
.
Как это видно, правила вычисления частных производных совпадают с правилами, указанными для функций одной переменной, и только требуется помнить, по какой переменной ищется производная.
Частные производные функции любого числа переменных определяются аналогично.
Пример. 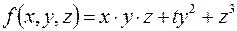 .
.
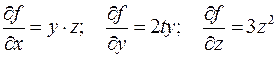 .
.
Частные производные 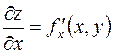 и
и 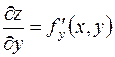 , вообще говоря, являются функциями переменных
, вообще говоря, являются функциями переменных 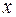 и
и 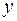 .
.
5.3. Если у функции 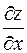 (у функции
(у функции 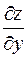 ) существует частная производная по переменной
) существует частная производная по переменной 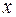 (по переменной
(по переменной 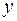 ), то ее называют частной производной второго порядка от функции
), то ее называют частной производной второго порядка от функции 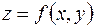 по переменной
по переменной 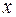 (по переменной
(по переменной 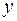 ) и обозначают
) и обозначают  (и
(и 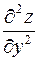 ) или
) или 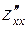 (и
(и 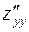 ).
).
Таким образом, по определению:
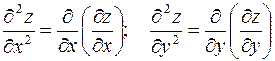 .
.
Если существует частная производная от функции 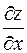 (от функции
(от функции 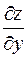 ) по переменной
) по переменной 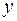 (по переменной
(по переменной 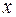 ), то эту производную называют смешанной частной производной второго порядка от функции
), то эту производную называют смешанной частной производной второго порядка от функции 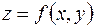 и обозначают символом
и обозначают символом
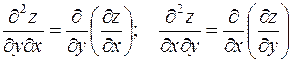 .
.
Как это видно для функции от двух переменных  , можно рассматривать четыре производных второго порядка.
, можно рассматривать четыре производных второго порядка.
Производные второго порядка можно снова дифференцировать как по 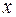 , так и по
, так и по 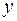 . Получим частные производные третьего порядка. Их будет уже восемь:
. Получим частные производные третьего порядка. Их будет уже восемь:
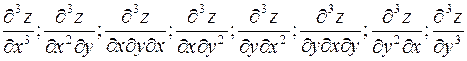 .
.
Вообще, частная производная 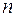 – го порядка есть первая производная от производной
– го порядка есть первая производная от производной 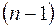 –го порядка. Например,
–го порядка. Например,
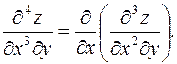
Естественно возникает вопрос, будут ли равны между собой частные производные, если они взяты по одним и тем же переменным одно и то же число раз, но в разном порядке. Например, равны ли
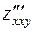 и
и 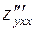 и
и 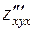 ?
?
В общем случае скажем: если нарушается непрерывность в точке 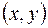 у этих производных, то ответ на этот вопрос отрицательный.
у этих производных, то ответ на этот вопрос отрицательный.
Пример.
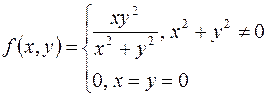 .
.
Вычислим частные производные этой функции:
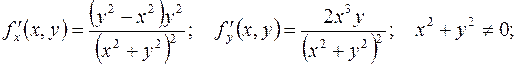
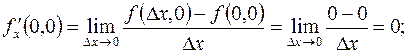
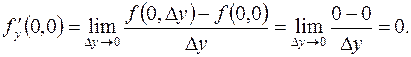
Аналогично вычисляются смешанные производные:
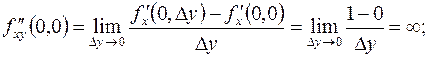

Таким образом, 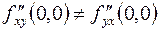 .
.
5.4 Теорема (о смешанных производных)
Пусть функция 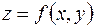 определена вместе со своими частными производными
определена вместе со своими частными производными 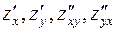 в некоторой
в некоторой  – окрестности точки
– окрестности точки 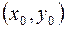 , причем
, причем 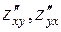 непрерывны в этой точке, тогда результат дифференцирования не зависит от порядка дифференцирования.
непрерывны в этой точке, тогда результат дифференцирования не зависит от порядка дифференцирования.
Пример. 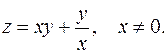
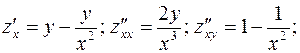
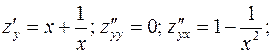
как видно, 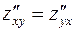 .
.
