Уравнение прямой с угловым коэффициентом. Угол между прямыми на плоскости
Обратимся к общему уравнению прямой
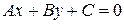 .
.
Если 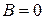 , то, как уже отмечалось, получаем уравнение прямой, параллельной оси ординат:
, то, как уже отмечалось, получаем уравнение прямой, параллельной оси ординат: 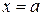 . Предположим, что данная прямая не параллельна оси ординат. Угол
. Предположим, что данная прямая не параллельна оси ординат. Угол 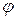 , отсчитываемый в положительном направлении (против часовой стрелки) от положительного направления оси абсцисс до данной прямой, называется углом наклона этой прямой. Число
, отсчитываемый в положительном направлении (против часовой стрелки) от положительного направления оси абсцисс до данной прямой, называется углом наклона этой прямой. Число
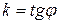
называется угловым коэффициентом прямой. Предположим, что угол наклона данной прямой – острый. Пусть 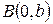 - точка пересечения прямой с осью ординат. Из прямоугольного треугольника видно, что точка
- точка пересечения прямой с осью ординат. Из прямоугольного треугольника видно, что точка 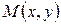 лежит на данной прямой тогда и только тогда, когда
лежит на данной прямой тогда и только тогда, когда
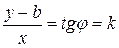 ,
,
если угол наклона прямой – острый, и тогда и только тогда, когда
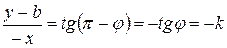 .
.
Таким образом, и в первом, и во втором случае получаем уравнение прямой
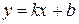 .
.
Такое уравнение называется уравнением данной прямой с угловым коэффициентом 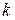 .
.
Рассмотрим задачу нахождения уравнения прямой с заданным угловым коэффициентом и проходящей через данную точку 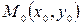 . Уравнение с угловым коэффициентом будет иметь вид
. Уравнение с угловым коэффициентом будет иметь вид 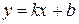 , где неизвестным остался коэффициент
, где неизвестным остался коэффициент 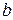 . Воспользуемся тем, что координаты точки
. Воспользуемся тем, что координаты точки 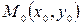 должны удовлетворять уравнению прямой:
должны удовлетворять уравнению прямой:
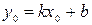
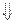
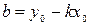 .
.
Таким образом, получаем следующее уравнение прямой:
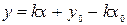
или
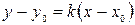 .
.
Рассмотрим вопрос о нахождении угла между прямыми. Если две прямые заданы своими общими уравнениями:
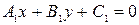 ,
,
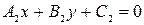 ,
,
то известны их векторы нормали: 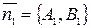 и
и 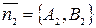 . Угол между прямыми равен углу между этими векторами, т.е. может быть найден по формуле:
. Угол между прямыми равен углу между этими векторами, т.е. может быть найден по формуле:
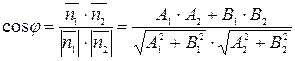 .
.
В частности, указанные прямые будут параллельны, если векторы нормали будут коллинеарны, т.е. когда координаты этих векторов будут пропорциональны:
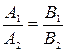 .
.
Рассматриваемые прямые будут перпендикулярны, если векторы нормали будут ортогональны, т.е. когда
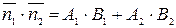 =0.
=0.
Если прямые заданы каноническими уравнениями, то по аналогии с предыдущим случаем угол между ними может быть найден как угол между их направляющими векторами.
Рассмотрим теперь случай, когда известны угловые коэффициенты 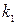 и
и 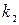 прямых. Очевидно, что угол
прямых. Очевидно, что угол 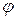 между этими прямыми равен разности
между этими прямыми равен разности 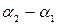 , где
, где 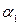 ,
, 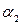 - углы наклона данных прямых. Тогда
- углы наклона данных прямых. Тогда
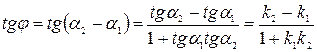 .
.
Эта формула и позволяет находить угол 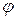 с помощью угловых коэффициентов. В частности, условие параллельности имеет вид:
с помощью угловых коэффициентов. В частности, условие параллельности имеет вид:
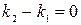
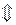
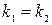 .
.
Перпендикулярность прямых равносильна равенству:
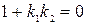
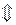
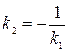 .
.
Пример.Найти угол между прямыми
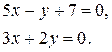
∆ Воспользуемся формулой для нахождения угла через коэффициенты общего уравнения:
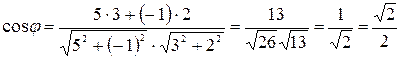 .
.
Следовательно, угол между прямыми равен 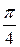 . ▲
. ▲
Пример.Найти прямую перпендикулярную к прямой
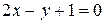 ,
,
и проходящую через точку 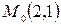 .
.
∆ Приведем уравнение данной прямой к уравнению с угловым коэффициентом:
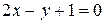
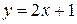 .
.
Следовательно, ее угловой коэффициент равен 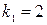 , а уравнение искомой прямой, перпендикулярной данной прямой равен
, а уравнение искомой прямой, перпендикулярной данной прямой равен
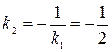 .
.
Теперь осталось воспользоваться уравнением прямой с заданным угловым коэффициентом, и проходящей через данную точку:
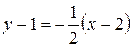 ,
,
Откуда получаем уравнение искомой прямой:
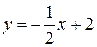 .
.
