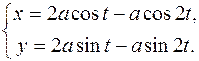Применение двойных интегралов

Найти двойным интегрированием объемы тел, ограниченных данными поверхностями:

1020. Плоскостями координат, плоскостями x = 4 и y = 4 и параболоидом вращения z = x² + y² + 1.

1021. Координатными плоскостями, плоскостью 2x + 3y – 12 = 0 и цилиндром .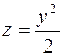

1022. Цилиндром z = 4 – x², координатными плоскостями и плоскостью 2x + y = 4 (x ³ 0).

1023. Цилиндром x² + y² = 2ax, параболоидом 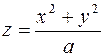и плоскостью z = 0 (a > 0).

1024. Параболоидом вращения z = x² + y² и плоскостями z = 0, y = 1, y = 2x и y = 6 – x.

1025. Цилиндрами 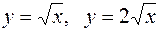и плоскостями z = 0 и x + z = 0.

1026. Цилиндром z = 9 – y², координатными плоскостями и плоскостью 3x + 4y = 12 (y ³ 0).

1027. Цилиндром x² + y² = R², параболоидом Rz = 2R² + x² + y² и плоскостью z = 0.

Тройные интегралы

1028. Перейти к цилиндрическим координатам в тройном интеграле 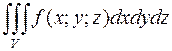и расставить пределы интегрирования, где V – область, ограниченная цилиндром x² + y² = 2x, плоскостью z = 0 и параболоидом z = x² + y².

В следующих примерах вычислить интегралы с помощью перехода к цилиндрическим или к сферическим координатам.

1029. 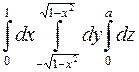; 1030. ;

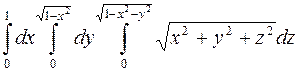1031. 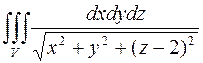, где v – цилиндр x² + y² £ 1, –1 £ z £ 1.

1032. Перейти к цилиндрическим координатам в тройном интеграле 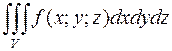и расставить пределы интегрирования, где V – область, находящаяся в первом октанте и ограниченная цилиндром x² + y² = R ² и плоскостями z = 0, z = 1, y = x, .

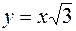В следующих примерах вычислить интегралы с помощью перехода к цилиндрическим или к сферическим координатам.

1033. 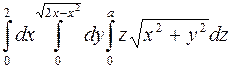; 1034. ;

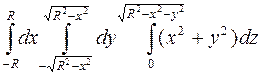1035. 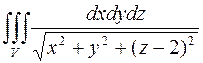, где v – шар x² + y² + z² £ 1.

Применение тройных интегралов. Площадь поверхности

Вычислить тройным интегрированием объемы тел, ограниченных поверхностями:

1036. Параболоидами z = x² + y² и z = x² + 2y² и плоскостями y = x, y = 2x и x = 1.

1037. Сферой x² + y² + z² = 4 и параболоидом x² + y² = 3z.

1038. Найти площадь части конуса z² = x² + y², лежащую над плоскостью Oxy и отсеченную плоскостью .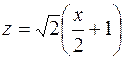

1039. Найти площадь части сферы x² + y² + z² = a², вырезанной цилиндром x² + y² = R² (R £ a).

Вычислить тройным интегрированием объемы тел, ограниченных поверхностями:

1040. Параболоидами z = x² + y² и z = 2x² + 2y², цилиндром y = x² и плоскостью y = x.

1041. Сферой x² + y² + z² = R² и параболоидом x² + y² = R(R – 2z) (z ³ 0).

1042. Найти площадь части конуса z² = x² + y², вырезанной цилиндром z² = 2py.

1043. Найти площадь части сферы x² + y² + z² = a², вырезанной цилиндром x² + y² = Rx.

Формула Грина

1044. Криволинейный интеграл 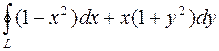по замкнутому контуру L, взятый в положительном направлении, преобразовать в двойной интеграл по области, ограниченной этим контуром.

1045. С помощью формулы Грина вычислить разность I₂ – I₁ между интегралам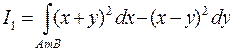и и 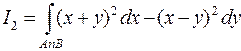, где AmB – отрезок прямой, соединяющей точки A(0; 0) и B(1; 1), а AnB – дуга параболы y = x².

1046. Вычислить криволинейный интеграл 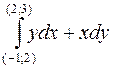от полного дифференциала.

Найти функции по данным полным дифференциалам:

1047. 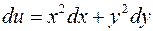. 1048. .

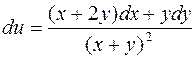1049. При помощи криволинейного интеграла вычислить площадь фигуры, ограниченной астроидой .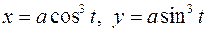

1050. Криволинейный интеграл 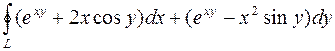по замкнутому контуру L, взятый в положительном направлении, преобразовать в двойной интеграл по области, ограниченной этим контуром.

1051. Вычислить 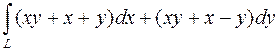, где L: 1) эллипс 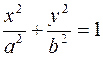; 2) окружность 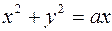. Интегрирование ведется в положительном направлении. (Вычисление провести двумя способами: 1) непосредственно, 2) с помощью формулы Грина.)

1052. Вычислить криволинейный интеграл 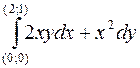от полного дифференциала.

Найти функции по данным полным дифференциалам:

1053. 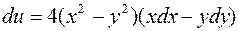. 1054. .

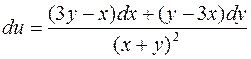1055. При помощи криволинейного интеграла вычислить площадь фигуры, ограниченной кардиоидой