Теорема о структуре общего решения линейного однородного диф. Уравнения n-го порядка. Характеристическое уравнение
Линейным однородным уравнением n-го порядка называют уравнение вида
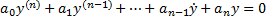 a – заданные непрерывные функции относительно x, так же коэффициенты уравнения.
a – заданные непрерывные функции относительно x, так же коэффициенты уравнения.
Частные решения y1=y1(x) , y2=y2(x), …, yn=yn(x) уравнения образуют фундаментальную систему некотором интервале , если всюду в этом интервале отличен от нуля определитель Вронского
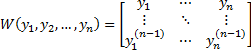 .
.
Ø С постоянными коэффициентамит.е. 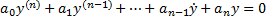
a – заданные действительные числа
Общее решение будет y=C1y1(x)+C2y2(x)+…+Cnyn(x)=0 y1(x) ,y2(x),…, yn(x) - частные решения уравнения, образующие фундаментальную систему в рассматриваемом интервале т.е. всюду отличен от нуля определитель Вронского. Частные решения будем искать в виде y=ekx
Подставив в уравнение и преобразовав получим характеристическое уравнение
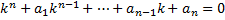
Уравнение имеет n решений. Эти корни будут действительными (простыми или кратными) или комплексными (простыми или кратными). Если комплексное число α+iβ является корнем, то сопряжённое число α -iβ тоже является корнем, так как уравнение имеет действительные коэффициенты.
· Каждому простому действительному корню k характеристического уравнения соответствует одно решение ekx исходного уравнения .
· Каждому действительному корню k кратности r характеристического уравнения отвечают r решений исходного уравнения вида ekx, xekx, x2ekx, …, xr-1ekx исходного уравнения
· Каждой паре комплексно сопряжённых корней k1= α+iβ и k2= α-iβ характеристического уравнения соответствует одна пара частных решений исходного уравнения
eαxcosβx и ieαxsinβx
· Каждой паре комплексно сопряжённых корней кратности μ k1= α+iβ и k2= α-iβ характеристического уравнения отвечают μ пар решений исходного уравнения
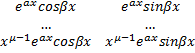
11. Теорема о структуре общего решения линейного неоднородного диф. Уравнения второго порядка.
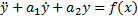
Общее решение данного уравнения представляется в виде суммы какого-либо частного решения y*=y*(x) этого уравнения и и общего решения 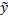 соответствующего однородного уравнения т.е.
соответствующего однородного уравнения т.е.
y= y*+ 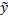 или y= y*(x) +C1y1(x)+C2y2(x)
или y= y*(x) +C1y1(x)+C2y2(x)
Для доказательства нужно два факта:
1) Сумма y*+ 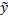 удовлетворяет исходному уравнению при любых значениях входящих в него постоянных С1 и С2.
удовлетворяет исходному уравнению при любых значениях входящих в него постоянных С1 и С2.
Подставляя данную сумму в исходное уравнение получим
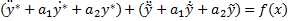 но
но 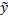 - общее решение соответствующего однородного уравнения следовательно вторая скобка обращается нуль, а первая скобка равна f(x). Таким образом получаем тождество, что означает данная сумма удовлетворяет исходному уравнению.
- общее решение соответствующего однородного уравнения следовательно вторая скобка обращается нуль, а первая скобка равна f(x). Таким образом получаем тождество, что означает данная сумма удовлетворяет исходному уравнению.
2) Для любых начальных условий можно подобрать такие значения постоянных С1 и С2 , при которых функция y= y*(x) +C1y1(x)+C2y2(x) будет удовлетворять этим начальным условиям.
Через определитель Вронского начальных условий
12. Метод вариации произвольных постоянных для нахождения частного решения линейного неоднородного уравнения второго порядка.
y*= C1(x)y1 +C2(x)y2 , где C1(x) и C2(x) – новые искомые функции. Одну из них можно выбрать произвольно или наложить на неё дополнительные требования, а вторую выбрать так чтобы функция y*= C1(x)y1 +C2(x)y2 была решением неоднородного уравнения.
Возьмём производную и получим 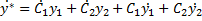 возьмём что
возьмём что 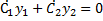
Тогда 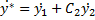 . Возьмём ещё раз производную и представим представим что y* решение неоднородного уравнения т.е.
. Возьмём ещё раз производную и представим представим что y* решение неоднородного уравнения т.е. 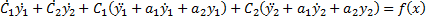
Но поскольку y1 и y2 – решения однородного уравнения суммы в скобках обращаются нуль получаем
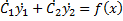 запишем вместе с
запишем вместе с 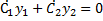 и получим систему двух линейных алгебраических уравнений для нахождения неизвестных
и получим систему двух линейных алгебраических уравнений для нахождения неизвестных 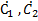 :
:
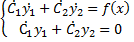 Решив систему найдём
Решив систему найдём 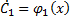 ,
, 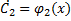 . Интегрируя получим:
. Интегрируя получим:
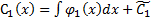 ,
, 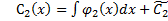 ,где
,где 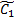 и
и 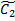 - произвольные постоянные, которые примем равные нулю. Подставляя найденное в y*= C1(x)y1 +C2(x)y2 получим искомое частное решение неоднородного уравнения y*=
- произвольные постоянные, которые примем равные нулю. Подставляя найденное в y*= C1(x)y1 +C2(x)y2 получим искомое частное решение неоднородного уравнения y*= 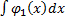 y1 +
y1 + 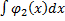 y2
y2
