Уравнение в полных дифференциалах

Интегрирующий множитель.

Определение 1.12. Уравнением в полных дифференциалах называется уравнение вида

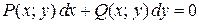, (1.6)

если его левая часть является полным дифференциалом некоторой функции 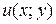, т.е.

.

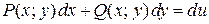В этом случае ДУ (1.6) можно записать в виде 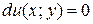, тогда его общий интеграл будет .

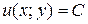Сформулируем условие в виде теоремы (без доказательства), по которому можно судить о том, что уравнение (1.6) является ДУ в полных дифференциалах.

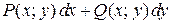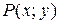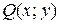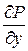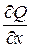Теорема 1.2. Для того, чтобы выражение было полным дифференциалом, где функции и и их частные производные и непрерывны в некоторой области 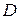плоскости 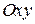, необходимо и достаточно выполнение условия

.

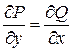При решении ДУ вида (1.6) сначала проверяется выполнение условия 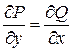. Далее функция 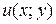может быть найдена из системы уравнений

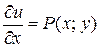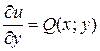, . (1.7)

Интегрируя первое из равенств (1.7) при фиксированном 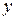и, учитывая, что произвольная постоянная может зависеть от 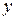, имеем

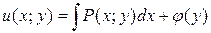. (1.8)

Затем из равенства

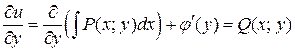
находим 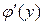, потом 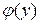. Подставляем 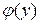в формулу (1.8), получаем общий интеграл уравнения .

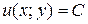Уравнение в полных дифференциалах не имеет особых решений.

Пример 1.9. Найти общий интеграл уравнения

.

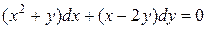Решение. Здесь 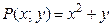, , 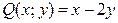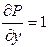и 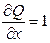. Следовательно, левая часть уравнения есть полный дифференциал некоторой функции 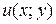, т.е.

,

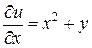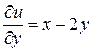
Проинтегрируем 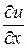по :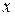

.

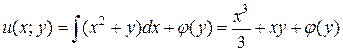Продифференцируем последнее выражение по 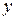: 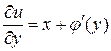. Получаем уравнение

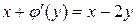Þ .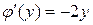

Откуда находим .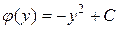

Таким образом,

.

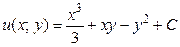Окончательно имеем: 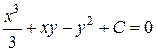-общий интеграл исходного уравнения.

,

Если уравнение (1.6) не является уравнением в полных дифференциалах 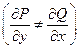, но существует функция 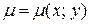, такая, что после умножения на нее обеих частей уравнения получается уравнение в полных дифференциалах, т.е.

,

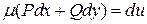то функция 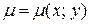называется интегрирующим множителем.

Если найден интегрирующий множитель 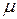, то интегрирование данного уравнения сводится к умножению обеих его частей на 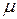, и отысканию общего интеграла полученного уравнения в полных дифференциалах.

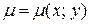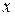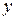Если - непрерывно-дифференцируемая функция от и , то

.

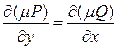Отсюда следует, что интегрирующий множитель 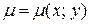удовлетворяет уравнению с частными производными первого порядка:

.

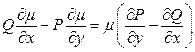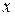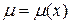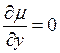Если интегрирующий множитель зависит только от , т.е. , то и в этом случае

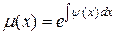, где .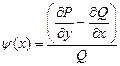

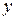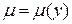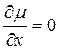Если интегрирующий множитель зависит только от , т.е. , то и в этом случае

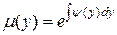, где .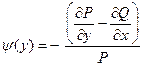

2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

ВЫСШИХ ПОРЯДКОВ

Основные понятия ДУ высших порядков

Как уже отмечалось выше, ДУ 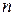-го порядка символически можно записать в виде

.

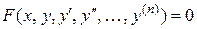Если ДУ 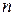-го порядка можно разрешить относительно 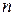-й производной, то ДУ будет иметь вид

.

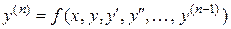В частности, ДУ второго порядка в общем случае записывается в виде 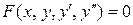, или, если это возможно, в виде, разрешенном относительно старшей производной, т.е. .

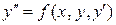Будем рассматривать только такие ДУ высших порядков, которые можно разрешить относительно высшей производной. Для этих уравнений имеет место теорема о существовании и единственности решения, аналогичная соответствующей теореме о решении ДУ первого порядка. Теорему примем без доказательства.

Теорема 2.1.Если в уравнении

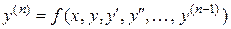
функция 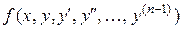и ее частная производные по аргументам 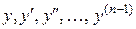непрерывны в некоторой области, содержащей значения

, , , …, ,

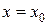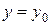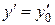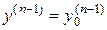то существует единственное решение 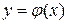уравнения, удовлетворяющее условиям

, , …, ,

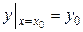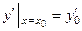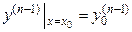которые называются начальными условиями.

Определение 2.1. Общим решением ДУ 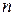-го порядка называется функция 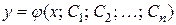, зависящая от 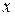и 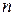произвольных постоянных .

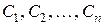Функция вида 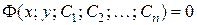, неявно определяющая общее решение, называется общим интегралом ДУ 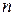-го порядка.

Определение 2.2. Всякая функция, получающаяся из общего решения при конкретных значениях постоянных 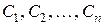, которые находятся из начальных условий, называется частным решением.

Решить (проинтегрировать) ДУ 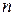-го порядка – значит:

1) найти его общее решение (если начальные условия не заданы);

2) найти то частное решение уравнения, которое удовлетворяет заданным начальным условиям.

ДУ высших порядков,