Пример решения и оформления задачи

Задача

Невесомая нерастяжимая нить перекинута через вращающийся около горизонтальной оси неподвижный блок. К концам нити привязаны грузы m₁ и m₂. При движении грузов сила давления блока на ось равна F, ускорение грузов а.

Массой блока и трением в оси можно пренебречь. Определить неизвестную величину в табл.2.

Таблица 2

m1, г	m2, г	F, Н	а, м/с2
		?	–

Решение

Движение грузов поступательное, поэтому их можно считать материальными точками. На каждый из рассматриваемых грузов действует сила тяжести ( 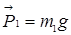и ) и 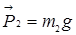сила натяжения нит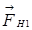и ( и 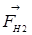), как показано на рисунке 1.

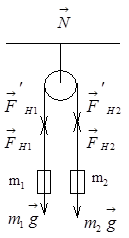
Схема приложения сил.

Второй закон Ньютона для каждого из грузов может быть записан следующим образом:

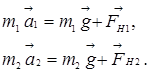
Невесомость нити (возможность пренебречь ее массой) позволяет считать силу натяжения вдоль всей нити постоянной. Неизменяемость силы натяжения при переходе через блок следует из того, что массой блока, следовательно, его моментом инерции, и трением в оси можно пренебречь, а потому разность моментов сил натяжения, действующих на блок с противоположных сторон, должна равняться нулю. Отсюда вытекает, что силы натяжения нити, действующие как на оба груза, так и на блок, можно считать равными между собой: .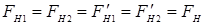

Не растяжимость нити позволяет найти связь между ускорениями грузов. Движение грузов происходит только в одном вертикальном направлении, поэтому достаточно рассматривать только одну координату у – будем отсчитывать ее вниз от оси блока (см. рисунок). Длина нити постоянна, поэтому: у₁+у₂=const.

Дифференцируя, получаем: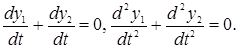

Здесь 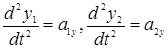. Ускорения грузов равны по абсолютной величине и противоположны по направлению. Обозначив ускорение груза m₁ через а, имеем: а_1у=–а_2у=а.

В уравнениях второго закона Ньютона перейдем от векторных соотношений к скалярным, взяв проекции всех векторов на ось у. Учитывая уже полученные соотношения между величинами, входящими в уравнения, имеем:

m₁a=m₁g–F_H ,

–m₂a=m₂g–F_H .

Отсюда можно найти а и F_H.

По условию задачи требуется найти силу давления блока на ось. На блок действуют две силы натяжения нити F¢_H1=F¢_H2 и сила реакции оси 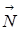(см. рисунок). Центр масс блока неподвижен, следовательно, сумма действующих на блок сил равна нулю:

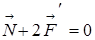; 2F_H–N=0 .

Отсюда N=2F_H. Согласно третьему закону Ньютона сила реакции оси равна по величине искомой силе давления F блока на ось. Решая уравнения, получаем:

; .

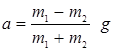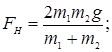
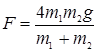Выразим данные задачи в системе СИ и проведем вычисления.

СИ m1= 0,65 кг, m2= 0,35 кг, g = 9,8 м/с2 ____________ F – ?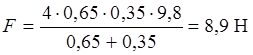

В соответствии с правилами приближенных вычислений результат округляем до двух значащих цифр. В ответ заносим значение силы F в ньютонах – число +8,900.

Проверка размерностей: .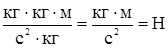

Анализ полученных результатов показывает, что значение силы натяжения нити F_H лежит между m₁g и m₂g. Сила давления блока на ось F при движении грузов меньше суммы сил тяжести, действующих на грузы. Равнодействующая сил, действующих на груз большей массы, направлена вниз, а сил, действующих на груз меньшей массы, – вверх. Поэтому ускорение груза большей массы направлено вниз, а ускорение груза меньшей массы – вверх.

Если массы грузов одинаковы (m₁=m₂), то сила натяжения нити равна силе тяжести, действующей на каждый груз, и ускорения грузов равны нулю. В этом случае грузы находятся в покое или движется равномерно, и сила давления блока на ось F равна 2mg – равномерное движение грузов не меняет величину силы давления блока на ось.

ГЛАВА 1

МЕХАНИКА

Задача 1.01

Тело брошено со скоростью v₀ с высоты h вверх под углом a к горизонту и упало на землю через промежуток времени t на расстояние l (по горизонтали) от места падения. Определить неизвестную величину в табл.3.

Таблица 3

Шифр	v0, м/с	a, град	h, м	t, с	l, м
	–		?	3,2
	?		2,4	–
		?	7,5	4,1	–
				–	?
	–			?

Задача 1.02

Тело брошено с башни высотой h вверх под углом к горизонту с начальной скоростью v₀. Дальность бросания (по горизонтали) равна l, скорость в момент падения на землю v. Определить неизвестную величину в табл.4.

Таблица 4

Шифр	h, м	a, град	v0, м/с	l, м	v, м/с
		?			–
			?		–
				?	–
	?				–
			–		?

Задача 1.03

С вершины холма, склон которого составляет с горизонтом угол b, брошен с начальной скоростью v₀ камень вверх под углом a к горизонту. Точка падения камня находится от вершины на расстоянии l (считая вдоль склона холма). Определить неизвестную величину в табл.5.

Таблица 5

Шифр	v0,м/с	a,град	b,град	l,м
				?
	?
				?
	?
				?

Задача 1.04

Волчок вращается вокруг своей оси симметрии с угловой скоростью w₁. Ось волчка с угловой скоростью w₂ описывает конус, образуя с вертикалью угол a. Полная угловая скорость волчка, равная по абсолютной величине w, составляет с вертикалью угол b. Определить неизвестную величину в табл.6.

Таблица 6

Шифр	w1, рад/с	w2, рад/с	a, град	w, рад/с	b, град
		4,5		–	?
		5,4	?		–
	–	3,7	7,5	?
	?	4,1		–	4,2
				?	–

Задача 1.05

Спутник движется по круговой орбите со скоростью v на расстоянии h от поверхности планеты. Масса планеты равна m=k∙m₃, где m₃– масса Земли. Радиус планеты равен R. Определить неизвестную величину в табл.7.

Таблица 7

Шифр	R, Мм	h, Мм	k=m/m3	v, км/с
		1,45	0,81	?
	1,74	?	0,012	1,5
	6,4	7,2		?
		?
	3,4		0,11	?

Задача 1.06

Через неподвижный блок, перекинута нить, к одному концу которой прикреплен груз m₁, а к другому – второй блок. Через второй блок также перекинута нить с грузами m₂ и m₃ на концах. Ускорения грузов равны соответственно a₁, a₂, a₃. Массами блоков и трением в них можно пренебречь. Ускорения считаются положительными, если они направлены вниз. Определить неизвестную величину в табл.8.

Таблица 8

Шифр	m1,кг	m2, кг	m3, кг	a1,м/с2	a2, м/с2	a3, м/с2
	7,2	–	?	–	0,9	–4,1
	–	?	5,1	1,2	0,6	–
	1,4	3,5	1,2	–	?	–
	?	1,2	2,1	0,8	–	–
	3,0			?	–	–

Задача 1.07

На верхнем конце наклонной плоскости укреплен легкий блок, через который перекинута нить с грузами m₁ и m₂ на концах. Груз m₁ скользит вниз по наклонной плоскости, поднимая висящий на другом конце груз m₂. Угол наклонной плоскости с горизонтом a, коэффициент трения между грузом m₁ и плоскостью равен k, ускорение a. Определить неизвестную величину в табл.9.

Таблица 9

Шифр	m1,кг	m2,кг	a, град	k	a, м/с2
	6,7	?		0,2	0,4
	?	2,3		0,1	0,45
	1,7	0,7		?	2,1
	7,4	3,8	?	0,3	0,84
	5,1	2,5		0,1	?

Задача 1.08

На разных склонах наклонной плоскости, образующих с горизонтом углы a₁ и a₂, находятся грузы m₁ и m₂. Нить, связывающая грузы, перекинута через легкий блок, укрепленный на вершине наклонной плоскости. Коэффициент трения между грузами и плоскостью равен k, ускорение груза a. Определить неизвестную величину в табл.10.

Таблица 10

Шифр	a1, град	a2, град	m1, кг	m2, кг	k	a, м/с2
			2,2	4,3	0,17	?
			?	7,9	0,2	1,3
			1,6	1,5	?	0,24
			4,8	5,6	0,15	?
			3,3	?	0,1	–2

Задача 1.09

На гладком горизонтальном столе лежат один на другом два бруска массами m₁ и m_2. Коэффициент трения между брусками равен k. К нижнему бруску, масса которого m₁, приложена постоянная горизонтальная сила F. Ускорения брусков равны соответственно a₁ и a₂. Определить неизвестную величину в табл.11.

Таблица 11

Шифр	m1, кг	m2, кг	k	F, Н	a1, м/с2	a2, м/с2
	5,6	?	–	2,9	0,4	0,3
	?	3,7	0,1		0,2	–
	2,6	?	0,15	4,3	–	1,1
	0,62	0,27	0,25	2,8	–	?
	3,2	2,1	0,1	2,1	?	–

Задача 1.10

По наклонной плоскости с углом a соскальзывает доска массой m₁, на которой находится брусок массой m₂. Коэффициент трения между наклонной плоскостью и доской равен k₁, а между доской и бруском k₂. Ускорение доски равно a₁, ускорение бруска a₂. Определить неизвестную величину в табл.12.

Таблица 12

Шифр	a, град	m1, кг	m2, кг	k1	k2	a1, м/с2	a2, м/с2
		4,8	4,5	0,15	–	?	3,6
		–	–	0,11	0,15	–	?
		4,7	3,4	?	0,05		–
		5,2	?	0,2	–	4,7	5,4
		2,6	1,1	0,4	0,1	?	–

Задача 1.11

Шарик массой m падает на горизонтальную поверхность стола с высоты h₁ и, отскочив, поднимается на высоту h₂. Время соударения равно t, средняя сила взаимодействия шарика со столом F. Определить неизвестную величину в табл.13.

Таблица 13

Шифр	m, г	h1, м	h2, м	t, мс	F, Н
		?	0,35	0,045
		1,7	1,4	?
	?	1,9	1,5	0,18
		2,4	?	0,49
		1,35	0,75	0,6	?

Задача 1.12

Человек массой m₁, стоящий на одном конце первоначально покоящейся тележки m₂ и длиной l, прыгает со скоростью v относительно земли под углом a к горизонту и попадает на другой конец тележки. Массу колес, а также силы сопротивления движению тележки не учитывать. Определить неизвестную величину в табл.14.

Таблица 14

Шифр	m1, кг	m2, кг	l, м	v, м/с	a, град
		?	2,6
	?		5,2	6,5
			?
			3,1	5,5	?
				?

Задача 1.13

Шайба соскальзывает с высоты h₁ по наклонной плоскости с углом a₁ к горизонту, затем поднимается на другую наклонную плоскость с углом a₂ до высоты h₂. Коэффициент трения шайбы о плоскость равен k. Определить неизвестную величину в табл.15.

Таблица 15

Шифр	h1, м	a1, град	h2, м	a2, град	k
	?		12,6		0,15
					?
			?		0,05
	8,5		4,6	?	0,2
	15,2	?	9,4		0,1

Задача 1.14

Две лодки массами m₁ и m₂ идут параллельными курсами со скоростями v₁ и v₂. Когда лодки оказываются рядом, из каждой лодки в другую перекладывается мешок массой m, после чего лодки продолжаются двигаться параллельными курсами, но со скоростями U₁ и U₂. Определить неизвестную величину в табл.16.

Таблица 16

Шифр	m1, кг	m2, кг	v1, м/с	v2, м/с	m, кг	U1, м/с	U2, м/с
			–	?		–1,42	1,5
			?	–		–2,7	2,8
			1,31	–	?	1,16	–2,5
			–	–2		2,3	?
			1,6	–		?	4,6

Задача 1.15

Копром забивают сваю массой m₁ в грунт на глубину S при каждом ударе. Средняя сила сопротивления грунта F. Подъемная часть копра – груз массой m₂, свободно падающей на сваю с высоты h. Сразу после удара груз и свая имеют скорость U. Масса копра больше массы сваи. Определить неизвестную величину в табл.17.

Таблица 17

Шифр	m1, кг	S, см	F, кН	m2, кг	h, м	U, м/с
			?		2,3	–
	?				1,9	–
		?			–	1,1
					?	–
					–	?

Задача 1.16

Два шарика массами m₁ и m₂, подвешенные на нитях одинаковой длины l, касаются друг друга. Первый шарик отклоняют на высоту h и отпускают, после чего происходит упругий центральный удар. Углы отклонения нитей после удара a₁ и a₂. Угол a₁ отрицателен, если шарик после удара отклоняется назад. Определить неизвестную величину в табл.18.

Таблица 18

Шифр	m1, кг	m2, кг	l, см	h, см	a1, град	a2, град
	0,17	0,32	?		–
	?	0,18			–2,1	–
	0,43	0,12			–	?
	0,058	?			–	4,3
	0,12	0,75			?	–

Задача 1.17

Снаряд, летящий со скоростью v, разрывается на два осколка массами m₁ и m₂, разлетающихся под углом a со скоростями U₁ и U₂. Определить неизвестную величину в табл.19.

Таблица 19

Шифр	v, м/с	m1, кг	m2, кг	a, град	U1, м/с	U2, м/с
			–			?
		–			?
	?			–
		?			–
		–		?

Задача 1.18

Частица массы, летящая со скоростью v₁, испытывает упругое нецентральное столкновение с покоящейся частицы массы m₂. После столкновения частицы разлетаются под углом a со скоростями U₁ и U₂. Определить неизвестную величину в табл.20.

Таблица 20

Шифр	m2/m1	v1, км/с	a, град	U1, км/с	U2, км/с
	–			?
			–		?
		–	?
	?	–
				?	–

Задача 1.19

Шкив с моментом инерции I имеет две цилиндрические ступени радиусами R₁ и R₂. На цилиндры намотаны в противоположных направлениях нити с грузами m₁ и m₂ на концах. Угловое ускорение шкива равно b, причем b>0, если груз m₁ опускается. Определить неизвестную величину в табл.21.

Таблица 21

Шифр	I, кг∙м2	R1, см	R2, см	m1, кг	m2, кг	b, рад/с2
	1,4			1,7	?	–1,5
	7,2			?	2,1	0,7
	0,4			0,63	0,48	?
	0,015	7,3	12,1	0,26	0,18	?
	?			0,5	0,75	–1,2

Задача 1.20

Человек массы m₁ находится на первоначально покоящейся горизонтальной платформе, представляющей собой однородный диск массы m₂ и радиуса R₂. Когда человек идет по окружности радиуса R₁ со скоростью v относительно платформы, сама платформа вращается вокруг вертикальной оси (без трения) с частотой оборотов n. Определить неизвестную величину в табл.22.

Таблица 22

Шифр	m1, кг	R1, м	m2, кг	R2, м	v, м/с	n, мин–1
		1,9		?	2,1	1,8
		1,9		2,8	?	3,1
		2,4	?	3,9	1,3	0,85
	?	2,7		3,5	2,3	2,5
		2,3		4,5	1,1	?

Задача 1.21

Шарик скатывается без проскальзывания с высоты h по одной наклонной плоскости и поднимается на другую. Углы плоскостей с горизонтом a₁ и a₂, скорость шарика в нижней точке равна v, время движения шарика до наивысшей точки падения t. Определить неизвестную величину в табл.23.

Таблица 23

Шифр	h, см	a1, град	a2, град	v, см/с	t, с
	–			?
	–		?
		?		–	3,2
	–			2,6	?
	?			–

Задача 1.22

Маленькие шарики массами m₁ и m_­2 (m₁>m₂) находятся на концах стержня длины l и массы m, который может вращаться вокруг горизонтальной оси, проходящей через середину стержня перпендикулярно к нему. Стержень приводят в горизонтальное положение и отпускают. Угловая скорость стержня при прохождении через вертикальное положение равна w. Определить неизвестную величину в табл.24.

Таблица 24

Шифр	m1, г	m2, г	m, г	l, см	w, рад/с
	?				3,2
				?	1,5
		?			2,3
			?		5,1
					?

Задача 1.23

Пуля массы m₁ летит со скоростью v, пробивает нижний конец доски массы m₂ и длины l и вылетает со скоростью U. Доска после попадания пули отклоняется от вертикали на угол a. Определить неизвестную величину в табл.25.

Таблица 25

Шифр	m1, г	v, м/с	U, м/с	m2, кг	l, см	a, град
	?			4,6		5,1
	5,6		?	2,8		6,3
	9,4			?		3,5
	8,2			17,5		?
	4,5	?		1,1

Задача 1.24

Тонкая квадратная пластинка со стороной a и массой m₁ может вращаться вокруг вертикальной оси, совпадающей с одной из ее сторон. В центр пластинки перпендикулярно к ней упруго ударяется шарик массой m_2, летящий со скоростью v. После удара скорость шарика U, угловая скорость пластинки w. U<0, если шарик после удара движется назад. Определить неизвестную величину в табл.26.

Таблица 26

Шифр	a, см	m1, кг	m2, г	v, м/с	U, м/с	w, рад/с
	–	1,2	?	4,1	–2,7	–
		?		–	–1,3	2,9
		1,9		7,8	–	?
		1,25		?	–
	–	0,48		3,5	?	–

ГЛАВА 2

МОЛЕКУЛЯРНАЯ ФИЗИКА. ТЕРМОДИНАМИКА

Задача 2.01

При температуре t давление газа равно P, средняя длина свободного пробега молекул l. Эффективное сечение молекулы газа равно s. Определить неизвестную величину в табл.27.

Таблица 27

Шифр	t, 0С	P, кПа	l, мкм	s∙1020, м2
		?	0,5
	?		0,04
	–13		?
		?
			?

Задача 2.02

При температуре t и давлении P молекула газа испытывает в единицу времени z соударений с другими молекулами. Масса киломоля газа m, эффективный диаметр молекулы d, средняя длина свободного пробега l. Определить неизвестную величину в табл.28.

Таблица 28

Шифр	t, 0С	P, мм.рт.ст.	z×10–9, с–1	m, кг/кмоль	d, нм	l, нм
			?		0,28	–
	–106		–	–	0,22	?
		?			0,36	–
	–45		?		0,38	–
	?		–	–	0,29

Задача 2.03

В баллоне объемом V находится смесь кислорода и гелия. Число молекул кислорода равно N₁, число молекул гелия N₂. Температура смеси равна T, давление P. Среднее значение молярной массы смеси равно m. Определить неизвестную величину в табл.29.

Таблица 29

Шифр	V, м3	N1×10–21	N2×10–21	T,К	P, Па	m, г/моль
	0,45	–	8,4			?
	0,15	5,1	–	?
	0,31	?	–
	?	–	0,6
	0,25	6,6	0,9		?	–

Задача 2.04

В сосуде объемом V находится смесь двух газов: газ с молекулярной массой m₁, в количестве m₁ и газ с молекулярной массой m₂ в количестве m₂. При температуре t давление в сосуде P. Определить неизвестную величину в табл.30.

Таблица 30

Шифр	V, л	m1, г/моль	m1,г	m2, г/моль	m2, г	t, 0С	P, МПа
	4,1						?
	0,75		0,15		0,14	–15	?
	?		1,1		2,9		0,4
	4,5		4,2		?		0,17
	4,6					?	1,2

Задача 2.05

Смесь содержит m₁ двухатомного газа с молекулярной массой m₁ и m₂ трехатомного газа с молекулярной массой m₂. Удельные теплоемкости смеси при постоянном объеме и постоянном давлении равны C_v и C_p. Определить неизвестную величину в табл.31.

Таблица 31

Шифр	m1, г	m1, г/моль	m2, г	m2, г/моль	Cv, Дж/(кг×К)	Cp, Дж/(кг×К)
	?					–
			?		–
					–	?
					?	–
					–	?

Задача 2.06

Для смеси, содержащей m₁ двухатомного газа с молекулярной массой m₁ и m₂ одноатомного газа с молекулярной массой m₂, отношение теплоемкостей при постоянном давлении и постоянном объеме равно g. Определить неизвестную величину в табл.32.

Таблица 32

Шифр	m1, г	m1, г/моль	m2, г	m2, г/моль	g
		–			1,6
					?
				?	1,49
	–				1,55
			–		1,45

Задача 2.07

В цилиндре под невесомым поршнем находился воздух в объеме V₁ при температуре t₁ и атмосферном давлении P₁. После погружения цилиндра в воду с температурой t₂ на глубину h объем воздуха уменьшится до V₂. Определить неизвестную величину в табл.33.

Таблица 33

Шифр	V1, л	P1, мм.рт.ст.	t1, 0С	V2, л	h, м	t2, 0С
	9,3		–3	?	4,5
	?			2,5	8,5
	0,39		?	0,34	1,5
	6,1			3,7		?
	2,4			1,9	?

Задача 2.08

Два сосуда соединены трубкой с краном. В одном находится кислород массой m₁ под давлением P₁,а в другом – углекислый газ массой m₂ под давлением P₂. После открывания крана и перемешивания газов давление смеси стало равным P. Температура газов до и после перемешивания одинакова. Определить неизвестную величину в табл.34.

Таблица 34

Шифр	m1, кг	P1, кПа	m2, кг	P2, кПа	P, кПа
	4,7		2,9	?
			?
	?		2,5
	2,3	?	3,9
	1,8		4,3		?

Задача 2.09

Из баллона объемом V, содержащего сжатый воздух при давлении P₁ и температуре t₁ , постепенно выпускают некоторую массу воздуха m. После закрытия крана давление воздуха в баллоне равно P₂, температура t₂. Определить неизвестную величину в табл.35.

Таблица 35

Шифр	V, л	P1, МПа	t1, 0С	m, кг	P2, МПа	t2, 0С
		1,6		0,13	1,15	?
		0,42		?	0,18
		?	–60	2,1	4,3	–49
		3,9		0,48	?	–40
		8,3	?	2,6	3,5	–25

Задача 2.10

Из баллона объемом V, содержащего азот при температуре t₁ выпускают часть газа столь быстро, что теплообмен газа в баллоне с атмосферой за время выпуска не успевает произойти. Сразу после закрытия крана температура газа в баллоне равна t₂, давление P₂. Масса выпускаемого азота равна m. Определить неизвестную величину в табл.36.

Таблица 36

Шифр	V, л	t1, 0С	P2, МПа	t2, 0С	m, кг
			?		0,28
		?	3,7	–15	2,24
	?		0,6	–11	0,17
			?		0,35
			8,6		?

Задача 2.11

Два теплоизолированных сосуда одинакового объема соединены трубкой с краном. В одном сосуде находится кислород при давлении P₁ и температуре t₁, во втором – гелий при давлении P₂ и температуре t₂. Когда кран открыли и газы перемешались, давление смеси установилось равным P, а температура t. Определить неизвестную величину в табл.37.

Таблица 37

Шифр	P1, МПа	t1, 0С	P2, МПа	t2, 0С	P, МПа	t, 0С
	?	–19	0,4		–
	2,2		?	–42	–	–17
	3,9	–12	4,7		?	–
	?	–15	0,3		–
	0,35	–140	0,79		–	?

Задача 2.12

Идеальный газ с удельными теплоемкостями при постоянном давлении C_p и постоянном объеме C_v. (отношение теплоемкостей C_p/C_v=g) совершает политропный процесс с показателем политропы n. Удельная теплоемкость газа в этом процессе равна c. Определить неизвестную величину в табл.38.

Таблица 38

Шифр	Cp, кДж/(кг×К)	Cv, кДж/(кг×К)	g=Cp/Cv	n	с, кДж/(кг×К)
	–	?	1,67	1,3	–0,55
	1,95	–	1,1	?	2,6
	–	10,4	1,1	?	–7,5
	5,2	3,1	–	1,2	?
	0,91	0,5	–	2,3	?

Задача 2.13

Некоторая масса газа с двухатомными молекулами при давлении P₁ имела объем V₁, а при давлении P₂ – объем V₂. Переход от первого состояния ко второму был сделан в два этапа: сначала по изобаре, а затем по адиабате. При этом количество поглощенного газом тепла равнялась Q, приращение внутренний энергии DU, работа газа A. Определить неизвестную величину в табл.39.

Таблица 39

Шифр	P1, кПа	V1, м3	P2, кПа	V2, м3	Q, кДж	DU, кДж	A, кДж
	?	0,12		0,48	–		–
		1,3		1,47	–	–	?
		0,95		0,44	–	?	–
		0,8		0,82	?	–	–
		0,84	?	0,59	–960	–	–

Задача 2.14

Двухатомный газ при давлении P₁ имел объем V₁, а при давлении P₂ – объем V₂. Переход из первого состояния во второе был сделан в два этапа: сначала по изотерме, затем по изохоре. Количество поглощенного газом тепла равна Q, приращение внутренней энергии DU, работа газа A. Определить неизвестную величину в табл.40.

Таблица 40