Методы решения иррациональных уравнений

I) Метод возведения в четные степени (неравносильный переход нужна проверка) и нечетные степени (равносильный переход).

II) Уравнения вида 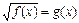решаются следующим образом.

Уравнению вида

соответствует равносильная система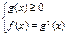

III) Уравнения вида 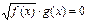решаются следующим образом.

Так как произведение равно нулю тогда и только тогда, когда один из множителей равен нулю, а остальные при этом имеют смысл, то данное уравнение равносильно следующей совокупности.

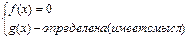или

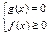
IV) Уравнения вида 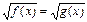решаются следующим образом.

Уравнению вида 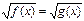соответствует равносильная система.

Способ №1 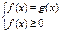Способ №2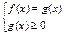

V) Уравнения вида 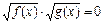решаются следующим образом.

Уравнению вида 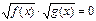соответствует равносильная система.

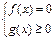или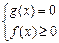

VI) Уравнения вида 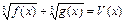решаются следующим образом.

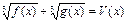
Возведем обе части уравнения в куб.

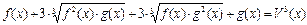
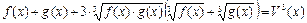(1)

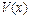
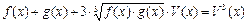(2)

При переходе из 1 в 2 происходит не равносильный переход, значит, необходима обязательная проверка.

VII) Уравнения вида 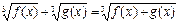решаются следующим образом.

Уравнению вида 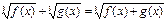соответствует равносильная совокупность систем.

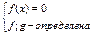
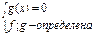
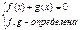
VIII) Уравнения вида 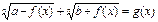решаются следующим образом.

Уравнению вида 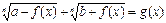решаются с помощью введения переменных.

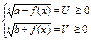
Сводятся к решению системы алгебраических уравнений.

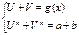
IX) Уравнения вида 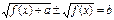решаются следующим образом.

Обе части исходного уравнения умножаются на выражение, сопряженное с левой частью уравнения и сложением затем исходного и полученного уравнений, что приводит к решению простейшего иррационального уравнения. (Нужна проверка)

X) Уравнения вида 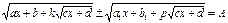решаются следующим образом.

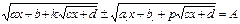
Удобно произвести замену.

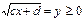
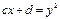
Исходное уравнение примет вид.

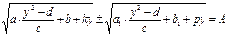
Обычно под знаком одного из радикалов, после такой замены, появляется полный квадрат двух члена.

XI) Уравнения вида 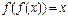решаются следующим образом.

Теорема. Если 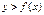- возрастающая функция, то уравнение 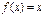и 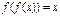-равносильны.

Например.

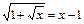
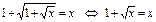
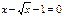
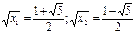
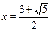решений нет

XII) Решение некоторых иррациональных уравнений можно свести к однородным уравнениям.

Например.

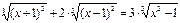
Пусть 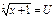, , 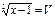тогда

Методы решения логарифмических неравенств.

1) Неравенства вида 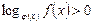решаются следующим образом.

Неравенству 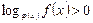соответствует равносильная систем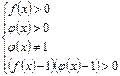а

2) Неравенства вида 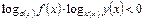решаются следующим образом.

Неравенству

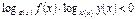
соответствует равносильная

система

3) Неравенства вида 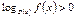решаются следующим образом.

Неравенству 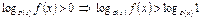соответствует два случая

I сл. 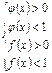II сл.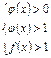

Методы решения показательно-степенных уравнений.

1) Уравнения вида 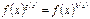решаются следующим образом.

Уравнению 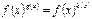соответствует пять случаев:

I.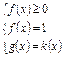

II. 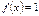– обязательно проверка.

III. 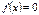– обязательно проверка.

IV. 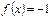– обязательно проверка.

V. 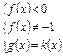– обязательно проверка.