Задачи на нахождение неизвестного слагаемого, уменьшаемого и вычитаемого

Решение этих задач выполняется на основе конкретного смысла дей­ствий сложения и вычитания и сводится к решению задач известных ви­дов - на нахождение суммы и остатка.

Подготовкой к введению этих задач является усвоение конкретного смысла действий сложения и вычитания, а также умение решать задачи на нахождение суммы и остатка.

При ознакомлении с каждой из задач на нахождения неизвестного компонента действий сложения и вычитания сначала выполняются соответствующие операции над множествами, которые связываются с действиями сложения и вычитания. При этом ученики под руководство» учителя объясняют выбор арифметического действия.

При решении задач на нахождение неизвестного слагаемого мы учим детей вести рассуждения примерно так:

Задача. Миша и Саша поймали 10 жуков. Миша поймал 6 жуков. Сколько жуков поймал Саша?

10 жуков - это те, что поймали Миша и Саша вместе. Всех жуков 10. Из этих 10 жуков 6 поймал Миша, а остальные Саша. Чтобы узнать, сколько жуков поймал Саша, надо из всех жуков отбросить те, что поймал Миша, то есть из 10 вычесть 6. Получится 4. Значит, Саша поймал 4 жука.

Проверим решение:

Если Миша поймал 6 жуков, а Саша -4, то вместе они поймали 6 + 4 = 10 (жуков). Значит, задача решена верно.

При решении задач на нахождение неизвестного уменьшаемого и вычитаемого целесообразно учить детей выделять главные опорные слова. Эти слова обычно показывают, что происходит с теми объектами, которые описываются в задаче.

Пример. В гараже стояло несколько машин. После того, как 3 маши, выехало из гаража, осталось 7 машин. Сколько машин было в гараже?

Было -?

Выехало – З м.

Осталось -7м.

В ходе беседы дети подводятся к пониманию того, что "были" - это те машины, которые выехали и остались. Поэтому для ответа на вопрос задачи необходимо действие сложения.

Подобные рассуждения сопровождаются наглядными демонстрациями, практическими действиями с дидактическим материалом. (Хорошо использовать прием, описанный в статье Рудницкой В.Н. Прием, облегчающий решение задач //НШ. - 1981. - №9. - С.31).

Вначале тексты задач этого вида составляет учитель по иллюстрациям, данным в учебнике или сделанным самим, затем вводятся текстовые задачи.

Задачи на разностное сравнение. Надо отметить, что это один из наиболее трудных для детей видов задач. Трудность для детей состоит в том, что они чаще ориентируются на отдельные слова, а в задачах этого вида в вопросе: "на сколько больше?" - слово "больше" их часто дезориентирует.

Главное при обучении решению задач этого вида - разъяснить детям, что задачи, где отвечаем на вопрос: "на сколько одно число больше другого или меньше?", решаются действием вычитания. При знакомстве с эти задачами можно использовать прием, предложенный Н.С.Поповой.

На доске прикрепляются 3 синихкружка и 5 красных.

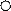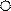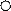Все кружки обводят мелом.

Считают, сколько синих - 3, сколько красных - 5.

Снимают по одному синему и красному кружку.

Осталось 2 красных.

Сколько сняли синих? - 3

Сколько сняли красных? - 3

Сколько красных осталось? - 2

Почему они остались? - их больше.

На сколько их больше? - на 2.

Сколько их было - 5.

Каким действием мы найдем 2, если было 5, сняли — З?

Вычитанием: 5 – 3 = 2.

Каких кружков было 5? - Красных.

Каких кружков было З? - Синих.

На сколько красных кружков больше, чем синих? -на 2.

Каким действием узнаем?

Вычитанием.

Аналогично с использованием счетного материала проводится срав­нение двух других чисел. Важно, чтобы дети каждый раз выполняли прак­тические действия, соответствующие вычитанию (убирали, отодвигали), и поняли, что из группы с большим количеством предметов убирается столько предметов, сколько их в меньшей группе. Затем делают обобще­ние: чтобы узнать, на сколько одно число больше или меньше другого, надо из большего числа вычесть меньшее.

При решении в дальнейшем таких задач надо использовать анало­гичные иллюстрации, обращая каждый раз внимание на то, что, находя, на сколько единиц одно число больше или меньше другого, надо из большего числа вычесть меньшее,

Задачи на увеличение или уменьшение числа на несколько единиц, выраженные в косвенной форме, рассматриваются в 3 классе по программе 1-3 или в 4 классе по программе 1-4.

Решение задач, выраженных в косвенной форме, вызывает определенные трудности у учащихся. При выборе действия они часто обращают внимание на слова "больше", "меньше", не вникая при этом в смысл текста задачи.

Чтобы предупредить возникновение такого рода ошибок, задачи на увеличение (уменьшение) числа на несколько единиц в прямой и косвенной форме следует решать парами.

При обучении решению этих задач надо учить детей анализировать текст задачи и задумываться над вопросами: какое число получится в результата решения - большее или меньшее, чем данное число. Полезно учить детей выполнять переформулировку задачи и выражать ее в прямой форме.

Большую помощь при обучении решению этих задач играет наглядность, схемы, чертежи.