Составить уравнение прямой, проходящей через точку А(-2, -3) и начало координат

Уравнение прямой имеет вид: 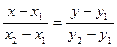, где х₁ = у₁ = 0; x₂ = -2; y₂ = -3.

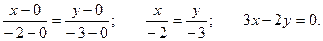
4.Определить угол между прямыми: y = -3x + 7; y = 2x + 1.

k₁ = -3; k₂ = 2 tgj = 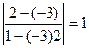; j = p/4.

5.Показать, что прямые 3х – 5у + 7 = 0 и 10х + 6у – 3 = 0 перпендикулярны.

Находим: k₁ = 3/5, k₂ = -5/3, k₁k₂ = -1, следовательно, прямые перпендикулярны.

6. Даны вершины треугольника А(0; 1), B(6; 5), C(12; -1). Найти уравнение высоты, проведенной из вершины С.

Находим уравнение стороны АВ: 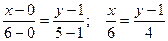; 4x = 6y – 6;

2x – 3y + 3 = 0;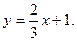

Искомое уравнение высоты имеет вид: Ax + By + C = 0 или y = kx + b.

k = 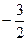. Тогда y = 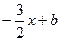. Т.к. высота проходит через точку С, то ее координаты удовлетворяют данному уравнению: 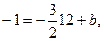откуда b = 17. Итого: .

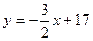Ответ: 3x + 2y – 34 = 0.

Тема №2-4. Кривые 2 порядка: окружность, эллипс,гипербола,парабола.

Построение кривых 2 порядка. Составление уравнений кривых 2-го порядка.

Кривая второго порядка задана уравнением Ах² + 2Вху + Су² + 2Dx + 2Ey + F = 0.

Существует система координат (не обязательно декартова прямоугольная), в которой данное уравнение может быть представлено в одном из видов, приведенных ниже.

1) 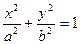- уравнение эллипса.

2) 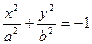- уравнение “мнимого” эллипса.

3) 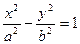- уравнение гиперболы.

4) a²x² – c²y² = 0 – уравнение двух пересекающихся прямых.

5) y² = 2px – уравнение параболы.

6) y² – a² = 0 – уравнение двух параллельных прямых.

7) y² + a² = 0 – уравнение двух “мнимых” параллельных прямых.

8) y² = 0 – пара совпадающих прямых.

9) (x – a)² + (y – b)² = R² – уравнение окружности.

Рассмотрим кривые 2 порядка: окружность, эллипс, гиперболу, параболу.Окружностью называется геометрическое место точек, равноудалённых от данной точки О, называемой центром окружности, на расстояние R . Число R > 0 называется радиусом окружности.

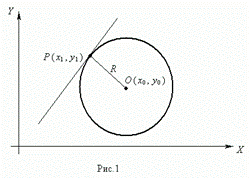
Уравнение окружности радиуса R с центром в точке О ( х₀ , у ₀ ) имеет вид:

( х – х₀ ) ² + ( у – у ₀ ) ² = R ² .

Если центр окружности совпадает с началом координат, то уравнение окружности упрощается:

х ² + у ² = R ² .

Пусть Р ( х₁ , у ₁ ) – точка окружности ( рис.1 ), тогда уравнение касательной к окружности в данной точке имеет вид:

( х₁ – х₀ ) ( х – х₀ ) + ( у₁ – у ₀ ) ( у – у ₀ ) = R ² .

Условие касания прямой y = m x + k и окружности х ² + у ² = R ² :

k ² / ( 1 + m ² ) = R ² .

Эллипс

Эллипсомназывается геометрическое место точек, сумма расстояний от которых до двух заданных точек F₁ и F₂ , называемых фокусами эллипса, есть величина постоянная.

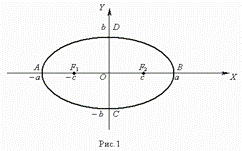
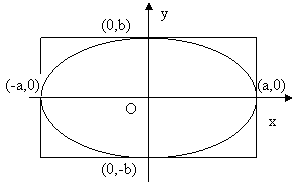
Уравнение эллипса( рис.1 ) :

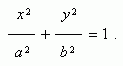
Здесь начало координат является центром симметрии эллипса, а оси координат – его осями симметрии. При a > b фокусы эллипса лежат на оси ОХ ( рис.1 ) , при a < b фокусы эллипса лежат на оси ОY , а при a = b эллипс становится окружностью ( фокусы эллипса в этом случае совпадают с центром окружности ). Таким образом, окружность есть частный случай эллипса.

Отрезок F₁F₂ = 2 с , где 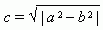, называется фокусным расстоянием. Отрезок AB = 2 a называется большой осью эллипса, а отрезок CD = 2 b – малой осью эллипса. Число e = c / a , e < 1 называется эксцентриситетом эллипса.

Пусть Р ( х₁ , у ₁ ) – точка эллипса, тогда уравнение касательной к эллипсув данной точке имеет вид:

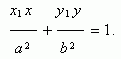
Условие касания прямой y = m x + k и эллипса х ² / a ² + у ² / b ² = 1 :

k ² = m ² a ² + b ² .

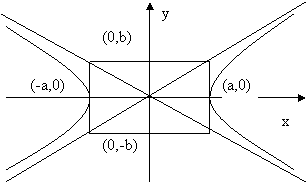
Гипербола

Гиперболой( рис.1 ) называется геометрическое место точек, модуль разности расстояний от которых до двух заданных точек F₁ и F₂ , называемых фокусами гиперболы, есть величина постоянная.

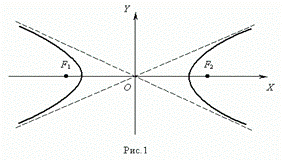
Уравнение гиперболы( рис.1 ) :

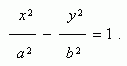
Здесь начало координат является центром симметрии гиперболы, а оси координат – её осями симметрии.

Отрезок F₁F₂ = 2 с , где 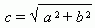, называется фокусным расстоянием. Отрезок AB = 2 a называется действительной осью гиперболы, а отрезок CD = 2 b – мнимой осью гиперболы. Число e = c / a , e > 1 называется эксцентриситетом гиперболы. Прямые y = ± ( b / a ) x называются асимптотами гиперболы.

Пусть Р ( х₁ , у ₁ ) – точка гиперболы, тогда уравнение касательной к гиперболев данной точке имеет вид:

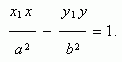
Условие касания прямой y = m x + k и гиперболы х ² / a ² – у ² / b ² = 1 :

k ² = m ² a ² – b ² .

Парабола

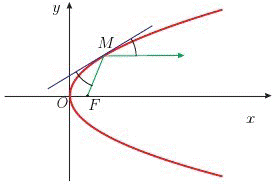
Параболой( рис.1 ) называется геометрическое место точек, равноудалённых от заданной точки F , называемой фокусом параболы, и данной прямой, не проходящей через эту точку и называемой директрисой параболы.

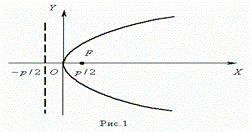
Уравнение параболы( рис.1 ) :

y ² = 2 p x .

Здесь ось ОХ является осью симметрии параболы.

Пусть Р ( х₁ , у ₁ ) – точка параболы, тогда уравнение касательной к параболев данной точке имеет вид:

у ₁ y = p ( x + х₁ ) .

Условие касания прямой y = m x + k и параболы y ² = 2 p x :

2 m k = p .

1.Найдите все параметры, характеризующие данные кривые второго порядка. Определите типы этих кривых, сделайте рисунки.
а) 9x² + 64y²=576
б) y²=6x

в) 9x²-16y²=144

Решение.

a) 9x²+ 64y² = 576 - уравнение эллипса

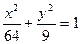- каноническое уравнение эллипса
a = 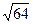= 8 и b = 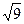= 3 - полуоси эллипса

Точки А(8,0), А'(-8,0), В(0,3), В'(0,-3) - вершины эллипса

с =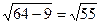

Точки F( 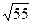,0) и F'(- 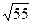,0) - фокусы эллипса

ε = с/а =( 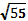)/8 - эксцентриситет эллипса

б) y² = 6x - уравнение параболы, симметричной относительно оси Ox,

т.е. прямая у = 0 - ось симметрии.
2р = 6
р = 3
Точка F(3/2,0) - фокус параболы.
Прямая х = -3/2 - директриса параболы

в) Приведем данное уравнение к каноническому виду (разделив его на 144):

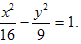
Отсюда следует, что a²=16, b²=9. Следовательно, a=4 -действительная полуось, b=3 - мнимая полуось. Тогда 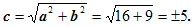Значит, фокусы имеют координаты F₁(-5,0), F₂(5,0). Находим эксцентриситет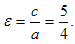
Уравнения асимптот имеют вид у = 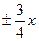, а уравнения директрис .

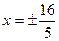2. Определить вид и расположение кривой

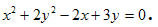
Решение.

Дополним члены, содержащие х и у соответственно, до полных квадратов:

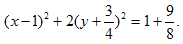
Отсюда получаем

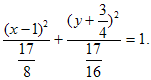
Следовательно, кривая, заданная исходным уравнением, представляет собой эллипс с полуосями

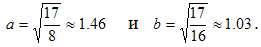
Центр эллипса находится в точке щ .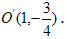

3. Найти координаты центра и радиус окружности x²+y²-6x+10y-15=0.

Решение.

В данном уравнении выделим полные квадраты, прибавляя и вычитая соответствующие числа. Получаем

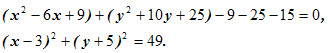
Отсюда находим а = 3, b= -5, R = 7.

Ответ: центр А(3;-5), радиус R=7.