Сложение и умножение вероятностей

Событие А называется частным случаем события В, если при наступлении А наступает и В. То, что А является частным случаем В, записываем .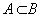

События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записываем А = В.

Суммой событий А и В называется событие А + В, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий: А или В.

Теорема о сложении вероятностей. Вероятность появления одного из двухнесовместных событий равна сумме вероятностей этих событий.

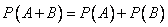
Заметим, что сформулированная теорема справедлива для любого числа несовместных событий:

.

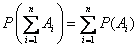Если случайные события 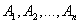образуют полную группу несовместных событий, то имеет место равенство

.

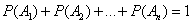Произведением событий А и В называется событие АВ, которое наступает тогда и только тогда, когда наступают оба события: А и В одновременно. Случайные события А и Bназываются совместными, если при данном испытании могут произойти оба эти события.

Теорема о сложении вероятностей 2. Вероятность суммы совместных событий вычисляется по формуле

.

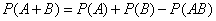События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Теорема об умножении вероятностей. Вероятность произведения независимых событий А и В вычисляется по формуле:

.

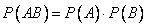Вероятность произведения зависимых событий вычисляется по формуле условной вероятности (см. следующий раздел).

Пример. В первом ящике 1 белый и 5 черных шаров, во втором 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Найти вероятность того, что один из вынутых шаров белый, а другой – черный.

Решение. Обозначим события: А – вынули белый шар из первого ящика,
;

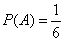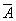- вынули черный шар из первого ящика,
;

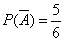В – белый шар из второго ящика,
;

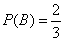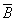- черный шар из второго ящика,
.

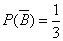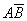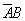Нам нужно, чтобы произошло одно из событий или . По теореме об умножении вероятностей
, .
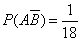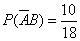Тогда искомая вероятность по теореме сложения будет
.

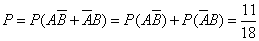Пример. Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9. Стрелки делают по выстрелу. Найти вероятность: а) двойного попадания; б) хотя бы одного попадания; г) одного попадания.

Решение.

Пусть А – попадание первого стрелка, ;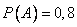

В – попадание второго стрелка, .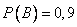

Тогда 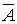- промах первого, ;

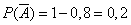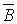- промах второго, .

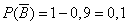Найдем нужные вероятности.

а) АВ – двойное попадание,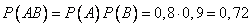

б) 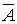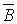– двойной промах, .

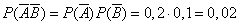в) А+В – хотя бы одно попадание,

.

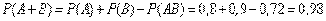г) 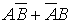– одно попадание,

.

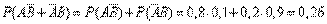Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8. Найти вероятности того, что формула содержится 1) только в одном справочнике; 2) только в двух справочниках; 3) во всех трех справочниках.

Решение.

А – формула содержится в первом справочнике;

В – формула содержится во втором справочнике;

С – формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

1.

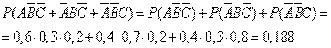
2. .

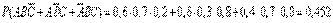3.

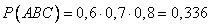
Пусть в результате испытания могут появиться n событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий? Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий. Ответ на поставленный вопрос дает следующая теорема.

Теорема. Вероятность появления хотя бы одного из событий 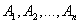, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий

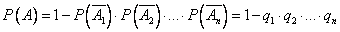
Если события 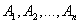имеют одинаковую вероятность 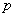, то формула принимает простой вид:

.

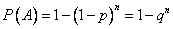Пример. Вероятности попадания в цель при стрельбе из трех орудий таковы: p1 = 0,8;p2 = 0,7; p3 = 0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий.

Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события 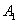(попадание первого орудия), 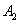(попадание второго орудия) и 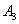(попадание третьего орудия) независимы в совокупности.

Вероятности событий, противоположных событиям 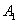, 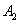и 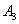(т. е. вероятности промахов), соответственно равны:

, ,

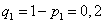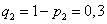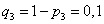
Искомая вероятность .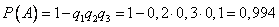

Пример. В типографии имеется 4 плоскопечатных машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина (событие А).

Решение. События "машина работает" и "машина не работает" (в данный момент) — противоположные, поэтому сумма их вероятностей равна единице: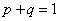

Отсюда вероятность того, что машина в данный момент не работает, равна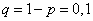

Искомая вероятность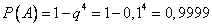

Так как полученная вероятность весьма близка к единице, то на основании следствия из принципа практической невозможности маловероятных событий мы вправе заключить, что в данный момент работает хотя бы одна из машин.

Пример. Вероятность того, что при одном выстреле стрелок попадает в цель, равна 0,4. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью не менее 0,9 он попал в цель хотя бы один раз?

Решение. Обозначим через А событие "при n выстрелах стрелок попадает в цель хотя бы один раз". События, состоящие в попадании в цель при первом, втором выстрелах и т. д., независимы в совокупности, поэтому применима формула .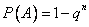

Приняв во внимание, что, по условию, 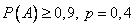(следовательно, 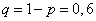), получим

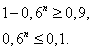
Прологарифмируем это неравенство по основанию 10:

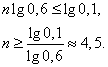
Итак, 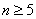, т.е. стрелок должен произвести не менее 5 выстрелов.

Условная вероятность

Случайное событие определено как событие, которое при осуществлении совокупности условий эксперимента может произойти или не произойти. Если при вычислении вероятности события никаких других ограничений, кроме условий эксперимента, не налагается, то такую вероятность называют безусловной; если же налагаются и другие дополнительные условия, то вероятность события называют условной. Например, часто вычисляют вероятность события В при дополнительном условии, что произошло событие А.

Условной вероятностью 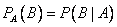(два обозначения) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.

Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т.е.

.

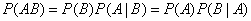В частности, отсюда получаем
.

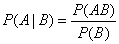Пример. В урне находятся 3 белых шара и 2 черных. Из урны вынимается один шар, а затем второй. Событие В – появление белого шара при первом вынимании. Событие А – появление белого шара при втором вынимании.

Решение. Очевидно, что вероятность события А, если событие В произошло, будет
.
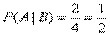Вероятность события А при условии, что событие В не произошло, будет
.

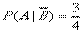Пример. В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Найти вероятность появления белого шара при втором испытании (событие В), если при первом испытании был извлечен черный шар (событие А).

Решение. После первого испытания в урне осталось 5 шаров, из них 3 белых. Искомая условная вероятность .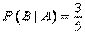

Этот же результат можно получить по формуле
.

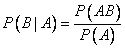Действительно, вероятность появления белого шара при первом испытании
.

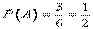Найдем вероятность 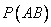того, что в первом испытании появится черный шар, а во втором — белый. Общее число исходов — совместного появления двух шаров, безразлично какого цвета, равно числу размещений 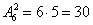. Из этого числа исходов событию 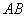благоприятствуют 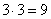исходов. Следовательно, .

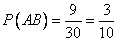Искомая условная вероятность

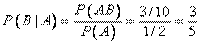
Результаты совпали.

Пример. В трамвайном парке имеются 15 трамваев маршрута №1 и 10 трамваев маршрута №2. Какова вероятность того, что вторым по счету на линию выйдет трамвай маршрута №1?

Решение. Пусть А - событие, состоящее в том, что на линию вышел трамвай маршрута №1, В - маршрута №2.

Рассмотрим все события, которые могут при этом быть (в условиях нашей задачи): 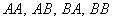. Из них нас будут интересовать только первое и третье, когда вторым выйдет трамвай маршрута №1.

Так как все эти события совместны, то:

;

;

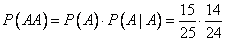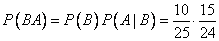отсюда искомая вероятность

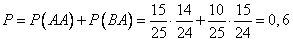
Пример. Какова вероятность того, что 2 карты, вынутые из колоды в 36 карт, окажутся одной масти?

Решение. Сначала подсчитаем вероятность того, что две карты окажутся одной определенной масти (например «пики»). Пусть А - появление первой карты такой масти, В- появление второй карты той же масти. Событие В зависит от события А, т.к. его вероятность меняется от того, произошло или нет событие А. Поэтому придется воспользоваться теоремой умножения в ее общей форме:

,
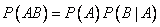где 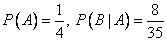(после вынимания первой карты осталось 35 карт, из них той же масти, что и первая - 8).

Получаем
.

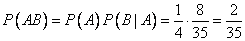События, состоящие в том, что будут вынуты две карты масти «пики», масти «треф» и т.д., несовместны друг с другом. Следовательно, для нахождения вероятности их объединения воспользуемся теоремой сложения:
.
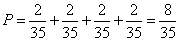