Применение алгебры булевых функций к релейно-контактным схемам
Рассмотрим электрические релейно-контакные схемы, главный элемент которых – электромагнитное реле.
Пусть x1, x2, ... , xn – набор контактов в схеме. Контакты могут быть размыкающими и замыкающими. Контакт называется замыкающим, если он замыкается при подаче напряжения. Контакт называется размыкающим, если он размыкается при подаче напряжения. Один и тот же контакт в схеме может быть как замыкающим, так и размыкающим.
Каждой последовательно- параллельной схеме сопоставим функцию проводимости:
f(x1, x2, ... , xn) =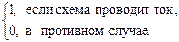 
Функция проводимости схемы, состоящей из одного элемента x, для замыкающего контакта есть f(x) = x, а для размыкающего контакта f(x) = Øx.
Функция проводимости схемы, состоящей из двух последовательно соединенных контактов x и y (рис. 4. 1) есть f(x, y) = x&y.
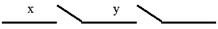
Рис. 4. 1
Функция проводимости схемы, состоящей из двух параллельно соединенных контактов x и y (рис. 4. 2) есть f(x, y) = x V y.
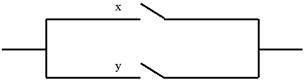
Рис. 4. 2
Каждой последовательно-параллельной схеме можно поставить в соответствие формулу логики булевых функций, реализующую функцию проводимости этой схемы. Две схемы считаются эквивалентными, если они имеют одинаковую функцию проводимости. Применяя равносильные преобразования, можно упрощать релейно-контактные схемы, заменяя их эквивалентными, с меньшим числом контактов.
Пример 4.22.
Найдем функцию проводимости схемы, изображенной на рис. 4. 3.
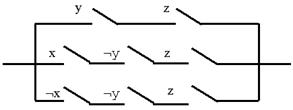
Рис. 4.3
f(x, y, z) = (y&z) V (x&Øy&z) V (Øx&Øy&z) º (y&z) V (Øy&z) º z.
Эквивалентная схема изображена на рис. 4.4.
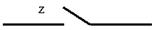
Рис 4.4
Контрольные вопросы к теме 4
1. Выберите правильный вариант ответа 1 – 4 для следующих вопросов:
а) Сколько существует различных булевых функций n переменных? б) Сколько существует различных наборов переменных для булевой функции n переменных?
Варианты ответа: 1) 2n; 2) 22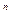 
; 3) n2; 4) n!.
2. Какое из следующих утверждений верно:
а) Переменные булевой функции и сама булева функция принимают значения 0 или 1;
б) Переменные булевой функции принимают значения 0 или 1, а значения самой булевой функции совпадают с множеством действительных чисел;
в) Значения переменных булевой функции совпадают с множеством действительных чисел, а сама булева функция принимает значения 0 или 1;
г) Значения переменных булевой функции и значения самой функции совпадают с множеством действительных чисел;
3. Выберите правильный вариант ответа 1 – 4 для следующих вопросов:
а) Сколько может быть различных ДНФ у булевой функции?
б) Сколько может быть различных СДНФ у булевой функции?
в) Сколько может быть различных КНФ у булевой функции?
г) Сколько может быть различных СКНФ у булевой функции?
Варианты ответа:
1 – ноль или одна; 2 – ноль или бесконечно много; 3 – ноль или одна; 4 – одна; 5 – одна или бесконечно много.
4. В какой из нормальных форм (ДНФ, СДНФ, КНФ, СКНФ) находится данная формула булевой функции трех переменных f(x, y, z):
а) xVy&z; б) x&y&z; в) (xVy)&(xVØz); г) xVyVz; д) Øx&y&z V y&Øz; е) xVØy; ж) x&z.
5. Какая релейно-контактная схема соответствует функции проводимости f(x) = (xVy)&(xVØz)?
Ответы на контрольные вопросы
Тема 1
1. Да.
2. Если А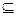 
В.
3. Пустое множество.
4. Да. Например, множество целых чисел эквивалентно множеству четных чисел.
5. Мощность множества точек отрезка [0, 1] больше. Это множество имеет мощность континнуума, а множество натуральных чисел является счетным множеством.
Тема 2.
1. Перечислением упорядоченных пар, указанием общего свойства упорядоченных пар, матрицей бинарного отношения.
2. Рефлексивного.
3. Для симметричного.
4. Для транзитивного.
5. Например, отношение параллельности прямых есть отношение эквивалентности. Пусть ax и ay – углы наклона прямых x и y с осью абсцисс. Тогда отношение r = {<x, y> çax £ ay} есть отношение частичного порядка.
6. Функция может быть задана таблицей, формулой, рекурсивной процедурой, с помощью описания.
7. б).
Тема 3.
1. б).
7. Нет. Только для неориентированного графа.
8. Нужно сложить все элементы матрицы и полученную сумму разделить на 2.
10. Нет.
11. а) и б).
12. Нет.
15. Да .
16. а), д)
17. г).
18. Нет.
19. Нет.
21. г).
22. n – 1.
23. Наименьшее – n – 1 (дерево), наибольшее – n( n – 1) ¤ 2 (полный граф).
24. Наименьшее – 0 (несвязный граф), наибольшее – n( n – 1) ¤ 2 (полный граф).
25. Нет.
27. Одну.
28. Нет.
29. Нахождение минимального пути.
30. Нахождение минимального пути.
31. Нахождение минимального остовного дерева.
32. Нахождение минимального остовного дерева.
33. Нахождение минимального остовного дерева.
34. Нахождение минимального остовного дерева.
Тема 4.
1. а)22 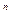; б) 2n.
2. а).
3. а) бесконечно много; б) ноль или одна; в) бесконечно много; г) ноль или одна.
4. а)ДНФ; б)ДНФ, СДНФ, КНФ; в)КНФ; г)ДНФ, КНФ, СКНФ; д)ДНФ; е)ДНФ, КНФ; ж)ДНФ, КНФ.
11. а) и б).