Интегралы, неберущиеся в элементарных функциях
Билет №1.
Первообразная функции и неопределенный интеграл.
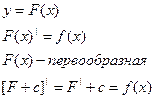
Терема:
Если F(x) яв –ся первообразной от фун-ции f(x), то и F(x)+c тоже яв-ся первообразной f(x).
Совокупность первообр. {F(x)+c} называют неопределенным итегралом.
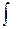-знак интеграла
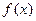- подинтегральная ф-ция;
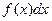- подинтегральное выражение;
x- переменная интегрирования;
c- постоянная;
Билет2.
Свойства неопределённого интеграла.
1) 
Док- во: 
2) 
3) 
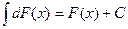Док-во: 
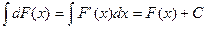(из определения диф-ла)
4) 
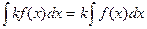Док-во: 
5) 
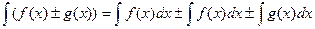
Док-во: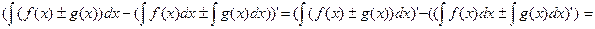 
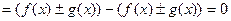
4),5)- линейные свойства неопределённого интеграла
Билет №3.
Интегралы от основных элементарных функций.(таблица)
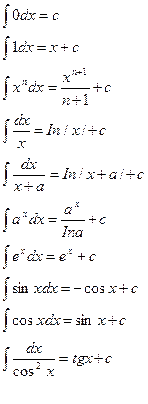
Билет №4.
Метод замены переменной в неопределённом интеграле
Теорема:
Если ф-ия x(t) диф-ма на мн- ве t 
T и сущ. 
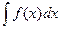, то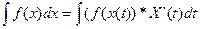 
Док- во:
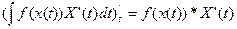
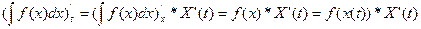
Билет 5.
Метод интегрирования по частям.
Теорема.
Пусть ф-ция u=u(x) дифференцируема на x X, а ф-ция v=v(x) интегрируема на мн-ве x, тогда справедлива формула интегрирования по частям:
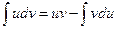
Док-во:
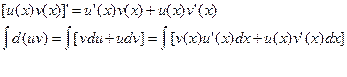
Типы интегралов:
1.
нужно применять формулу интегрирования по частям n раз
2.
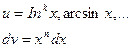
применять ф-лу k раз;
Билет №6.
Интегрирование простейших рациональных дробей
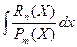
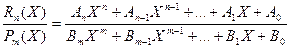
1)n>m=>неправильная дробь, нужно выделить у этой дроби целую часть и правильную дробь.
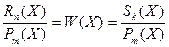, где W(X)- целая часть.
Метод вычёркивания можно использовать только в том случае, если знаменатель представлен в виде произведения полиномов первых степеней.
Билет №7.
Интегрирование некоторых видов иррациональностей.
Интегралы вида 
, 
.
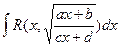а) -интегралы, подинтегральная
фун-ция кот-рых яв-ся иррациональной
ф-цией относительно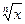 
.
б)
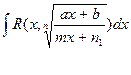
Билет №8.
Интеграл вида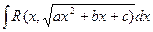 
Подстановка Эйлера: 1-ая подстановка: a>0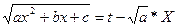 
X=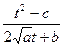 
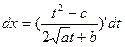
2-ая подстановка: с>0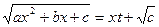 
(или 
)
Замечание: подстановки Эйлера не рекомендуются, если a>0 и c>0 одновременно.
3-ая подстановка: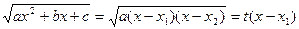 
Билет№9.
Интегрирование тригонометрических ф-ций.
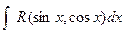-интегралы, к-рые считаются рациональными отностельно sinx и cosx.
Универсальная подстановка:
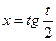
Замечание: универсальная подстановка приводит часто к громоздким вычислениям и , поэтому лучше использовать спец. приемы.
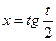
Билет №10.
Интегрирование иррациональных функций с помощью тригонометрических подстановок.
Замечание: универсальная подстановка хорошо применяется для интегралов вида: 
а в остальных случаях применение универсальной подстановки громоздко.
Интегралы вида: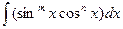 
1)если m- нечётное, n- чётное, то замена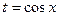 
2)если m- чётное, n- нечётное, то замена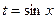 
3)если m,n- нечётные, то замена 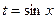или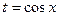
4)если m,n- чётные, то необходимо понизить степень при помощи формул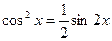 
; 
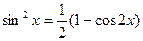и 
5)если m+n=-2k, гдеk>0 и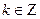 
m+n<0 , то замена t=tgx
Билет №11.
Интегрирование дифференциальных биномов.
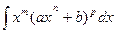
1)p 
x= 
, n- общий знаменатель дроби
2) 
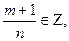
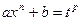общий знаменатель m и n
3) 
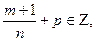
, где s- знаменатель p
Билет №12.
Интегралы, неберущиеся в элементарных функциях.
1) 
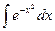- интеграл Пуассона (статистика) 2) 
-интегральный sin
3) 
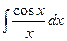-интегральный cos 4) 
-интеграл Френеля
5) 
-интеграл Френеля
Билет 13.