Равновесие тела при наличии трения качения
Рассмотрим цилиндр (каток), покоящийся на горизонтальной плоскости, когда на него действует горизонтальная активная сила 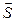 ; кроме нее, действуют силы тяжести
; кроме нее, действуют силы тяжести 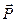 , а также нормальная реакция
, а также нормальная реакция 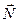 и сила трения
и сила трения 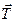 . Как показывает опыт, при достаточно малой величине силы
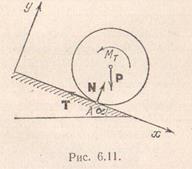
. Как показывает опыт, при достаточно малой величине силы 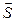 цилиндр остается в покое. Но этот факт нельзя объяснить, если удовлетвориться введением сил, изображенных на рис. Согласно этой схеме равновесие невозможно , так как главный момент всех сил, действующих на цилиндр
цилиндр остается в покое. Но этот факт нельзя объяснить, если удовлетвориться введением сил, изображенных на рис. Согласно этой схеме равновесие невозможно , так как главный момент всех сил, действующих на цилиндр 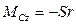 , отличен от нуля и одно из условий равновесия не выполняется.
, отличен от нуля и одно из условий равновесия не выполняется.
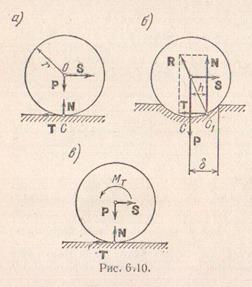 Причина выявившегося несоответствия состоит в том, что в наших рассуждениях мы продолжаем пользоваться представлением об абсолютно твердом теле и предполагаем касание цилиндра с поверхностью, происходящим по образующей. Для устранения отмеченного несоответствия теории с опытом необходимо отказаться от гипотезы абсолютно твердого тела и учесть, что в действительности цилиндр и плоскость вблизи точки С деформируются и существует некоторая площадь соприкосновения конечной ширины. Вследствие этого в ее правой части цилиндр прижимается сильнее, чем в левой, и полная реакция
Причина выявившегося несоответствия состоит в том, что в наших рассуждениях мы продолжаем пользоваться представлением об абсолютно твердом теле и предполагаем касание цилиндра с поверхностью, происходящим по образующей. Для устранения отмеченного несоответствия теории с опытом необходимо отказаться от гипотезы абсолютно твердого тела и учесть, что в действительности цилиндр и плоскость вблизи точки С деформируются и существует некоторая площадь соприкосновения конечной ширины. Вследствие этого в ее правой части цилиндр прижимается сильнее, чем в левой, и полная реакция 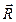 приложена правее точки С (точка
приложена правее точки С (точка 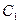 ).
).
Полученная теперь схема действующих сил статически удовлетворительна, так как момент пары 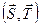 может уравновеситься моментом пары
может уравновеситься моментом пары 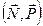 . Считая деформацию малой, заменим эту систему сил системой, изображенной на рис. В отличие от первой схемы, к цилиндру приложена пара сил с моментом
. Считая деформацию малой, заменим эту систему сил системой, изображенной на рис. В отличие от первой схемы, к цилиндру приложена пара сил с моментом
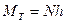 . (6.11) Этот момент называется моментом трения качения.
. (6.11) Этот момент называется моментом трения качения.
Составим уравнения равновесия цилиндра:
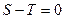 ,
,
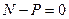 , (6.12)
, (6.12)
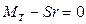 .
.
Первые два уравнения дают 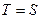 ,
, 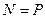 , а из третьего уравнения можно найти
, а из третьего уравнения можно найти 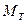 . Затем из (6.11) определяем расстояние между точками С и
. Затем из (6.11) определяем расстояние между точками С и 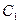 :
:
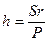 . (6.13) Как видно, с увеличением модуля активной силы
. (6.13) Как видно, с увеличением модуля активной силы 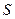 растет расстояние
растет расстояние 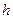 . Но это расстояние связано с площадью поверхности контакта и, следовательно, не может неограниченно увеличиваться. Это значит, что наступит такое состояние, когда увеличение силы
. Но это расстояние связано с площадью поверхности контакта и, следовательно, не может неограниченно увеличиваться. Это значит, что наступит такое состояние, когда увеличение силы 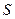 приведет к нарушению равновесия. Обозначим максимально возможную величину
приведет к нарушению равновесия. Обозначим максимально возможную величину 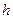 буквой
буквой 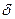 . Экспериментально установлено, что величина
. Экспериментально установлено, что величина 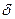 пропорциональна радиусу цилиндра и различна для разных материалов.
пропорциональна радиусу цилиндра и различна для разных материалов.
Следовательно, если имеет место равновесие, то выполняется условие
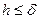 . (6.14)
. (6.14)
Величина 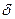 называется коэффициентом трения качения; она имеет размерность длины.
называется коэффициентом трения качения; она имеет размерность длины.
 Условие (6.14) можно также записать в виде
Условие (6.14) можно также записать в виде
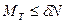 ,
,
или, учитывая (6.12),
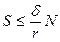 . (6.15)
. (6.15)
Очевидно, что максимальный момент трения качения 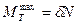 пропорционален силе нормального давления.
пропорционален силе нормального давления.
В справочных таблицах приводится отношение коэффициента трения качения к радиусу цилиндра 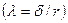 для различных материалов.
для различных материалов.
Задача 6.8.На наклонной плоскости находится цилиндр. Найти, при каких углах наклона плоскости к горизонту 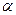 цилиндр будет находиться в равновесии, если
цилиндр будет находиться в равновесии, если 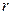 – радиус цилиндра,
– радиус цилиндра, 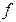 – коэффициент трения скольжения,
– коэффициент трения скольжения, 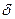 – коэффициент трения качения.
– коэффициент трения качения.
Составим уравнения равновесия:
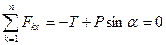 ,
,
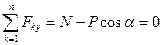 ,
,
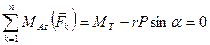 .
.
Кроме того, должны выполняться неравенства
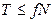 ,
, 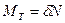 .
.
Из первых двух уравнений мы можем определить 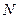 ,
, 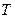 ,
, 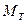 ; подставив эти величины в последние два неравенства, получим
; подставив эти величины в последние два неравенства, получим
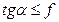 , (6.16)
, (6.16)
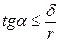 . (6.17)
. (6.17)
Эти неравенства должны удовлетворяться одновременно. В тех случаях, когда 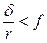 , потеря равновесия происходит путем перехода к качению, так как сначала нарушится неравенство (6.17); если же
, потеря равновесия происходит путем перехода к качению, так как сначала нарушится неравенство (6.17); если же 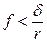 , то нарушится неравенство (6.16) и цилиндр начнет скользить.
, то нарушится неравенство (6.16) и цилиндр начнет скользить.
Глава 7
