Методы прямоугольников
Рассмотрим сначала простейшие методы из класса методов Ньютона-Котеса, когда подынтегральную функцию f(x) на интервале интегрирования заменяем полиномом нулевой степени. Подобная замена является неоднозначной, так как константу можно выбрать равной значению подынтегральной функции в любой точке в интервале интегрирования. Приближенное значение интеграла определится как площадь прямоугольника, одна из сторон которого есть длина отрезка интегрирования, а другая - аппроксимирующая константа.


Рис. 1. Метод левых прямоугольников. Рис.2. Метод правых прямоугольников
Методы левых (рис. 1) и правых прямоугольников (рис. 2) имеют сравнительно высокую погрешность. Запишем выражение для интеграла на интервале [хi, хi+ h], полученное методом средних прямоугольников
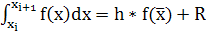 (3)
(3)
где 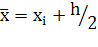 , R =
, R =  , и оценим погрешность R. Для этого разложим подынтегральную функцию f (х) в ряд Тейлора около средней точки
, и оценим погрешность R. Для этого разложим подынтегральную функцию f (х) в ряд Тейлора около средней точки 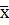
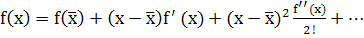 (4)
(4)
в малой окрестности точки х этот ряд с высокой точностью представляет функцию f(x) при небольшом количестве членов разложения. Поэтому, подставляя под интеграл вместо функции f(x) ее тейлоровское разложение (4) и интегрируя его почленно, можно вычислить интеграл с любой наперед заданной точностью
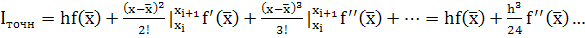 (5)
(5)
Сравнивая соотношения (3) и (5), можно записать выражение для погрешности R. При малой величине шага интегрирования h основной вклад в погрешность R будет вносить первое слагаемое, которое называется главным членом погрешности Roi вычисления интеграла на интервале [xi, xi+1]
 (6)
(6)
Главный член полной погрешности для интеграла на всем интервале [х0, хn] определится путем суммирования погрешностей на каждом частичном интервале [xi, xi+1]
 (7)
(7)
Формула (7) представляет собой теоретическую оценку погрешности вычисления интеграла методом средних прямоугольников, эта оценка является априорной, так как не требует знания значения вычисляемого интеграла. Степень шага h, которой пропорциональна величина 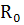 , называется порядком метода интегрирования. Метод средних прямоугольников имеет второй порядок.
, называется порядком метода интегрирования. Метод средних прямоугольников имеет второй порядок.
Аналогично проведем априорную оценку метода левых прямоугольников. Разложим подынтегральную функцию в ряд Тейлора около точки х= 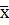 ,
,
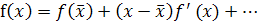 (8)
(8)
Интегрируя разложение (8) почленно на интервале [xi, xi+1], получим
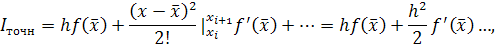
где первое слагаемое есть приближенное значение интеграла, вычисленное по методу левых прямоугольников, второе слагаемое является главным членом погрешности
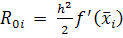 (9)
(9)
На интервале [х0, хn] главный член погрешности интегрирования получим суммированием частичных погрешностей (9)
 (10)
(10)
Таким образом, метод левых прямоугольников имеет первый порядок; кроме того, погрешность будет больше по сравнению с методом средних прямоугольников.
Метод трапеций.
Подынтегральную функцию заменим на участке [xi,xi+h] полиномом первой степени Р1(х) (рис. 1.4). Как и в методах прямоугольников, такая аппроксимация неоднозначна.
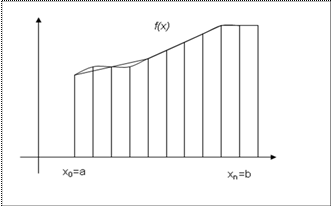
Рис.3. Метод трапеций.
В этом случае приближенное значение интеграла определяется площадью трапеции
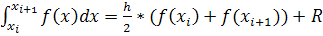 (11)
(11)
Априорную погрешность R метода трапеций получим путем интегрирования тейлоровского разложения подынтегральной функции около точки 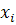 :
:
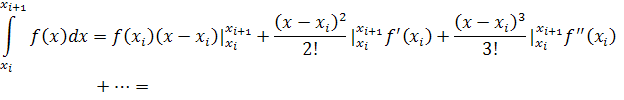
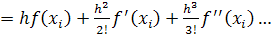 (1221)
(1221)
С помощью разложения вычислим подынтегральную функцию в точке xi + h
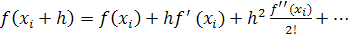 (13)
(13)
откуда
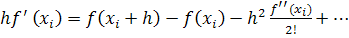 (14)
(14)
Подставляя произведение (14) в выражение (12), получим
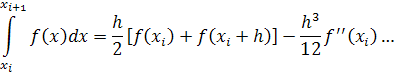
Следовательно, главный член погрешности метода трапеций на одном интервале будет
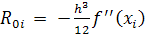 (15)
(15)
Если интегрирование проводится путем разбиения отрезка [х0, хn] на несколько интервалов, то общую погрешность получим суммированием частичных погрешностей (15)
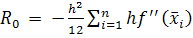 (16)
(16)
Метод трапеций, как и метод средних прямоугольников, имеет второй порядок. Если подынтегральная функция задана аналитически, то предпочтительнее из методов второго порядка применять метод средних прямоугольников.
Метод Симпсона.
Подынтегральную функцию f(x) заменим интерполяционным полиномом второй степени Р2(х), проходящим через узлы х0, х1, х2 (рис.5), тогда
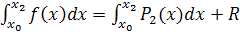 ,
,
где R - погрешность вычисления интеграла.
 э
э
Рис. 4. Метод Симпсона.
Для записи полинома Р2(х) воспользуемся интерполяционной формулой Ньютона для трех узлов
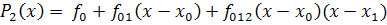 , (17)
, (17)
где
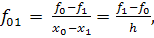
 - разделенные разности, h - расстояние между узлами. Введем новую переменную
- разделенные разности, h - расстояние между узлами. Введем новую переменную 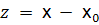 , тогда
, тогда 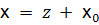 и полином (17) принимает вид
и полином (17) принимает вид
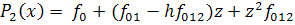 . (18)
. (18)
Теперь вычислим интеграл от полинома (18)
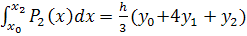 (19)
(19)
Последнее соотношение называют квадратурной формулой Симпсона, или формулой парабол.
Формулу Симпсона можно получить и с помощью первой и второй формул Рунге, примененных к вычислению интеграла методом трапеций. Запишем два приближенных значения интеграла от функции f(x) на интервале [хо,х2] с шагами h и 2h по формуле трапеций (11).
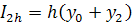 ,
,
 (20)
(20)
Получим уточненное значение интеграла
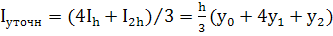 ,
,
которое совпадает с формулой Симпсона (19).
Для оценки погрешности формулы Симпсона разложим подынтегральную функцию f(x) в ряд Тейлора около точки хi и проинтегрируем разложение почленно в интервале [хо,х2].
Суммируя разложения около точки х1 для функции f(x) в узлах x0 и x2, получим, что
 ,
,
тогда
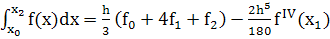 (21)
(21)
Первое слагаемое в правой части формулы (21) совпадает с формулой Симпсона, значит, второе слагаемое является главным членом погрешности для интеграла на интервале [хо,х2]
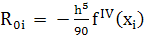 (22)
(22)
Полная погрешность запишется в виде
 (23)
(23)
Следовательно, формула Симпсона имеет четвертый порядок точности с очень малым численным коэффициентом в остаточном члене. Формула Симпсона позволяет получить высокую точность, если четвертая производная подынтегральной функции не слишком велика. В противном случае методы второго порядка могут дать большую точность, чем метод Симпсона.
