Экстремум функции двух переменных
Так же как и для функции одной переменной для функций нескольких переменных можно ввести понятия максимума и минимума. Рассмотрим этот вопрос применительно к функции двух переменных.
Определение 5.13.1. Функция 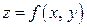 имеет максимум в точке
имеет максимум в точке 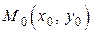 , принадлежащей области определения функции, если для всех точек
, принадлежащей области определения функции, если для всех точек 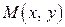 из этой области, расположенных в некоторой окрестности точки
из этой области, расположенных в некоторой окрестности точки 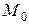 , выполнятся условие
, выполнятся условие 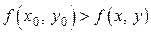 .
.
Определение 5.13.2. Функция 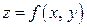 имеет минимум в точке
имеет минимум в точке 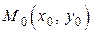 , принадлежащей области определения функции, если для всех точек
, принадлежащей области определения функции, если для всех точек 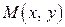 из этой области, расположенных в некоторой окрестности точки
из этой области, расположенных в некоторой окрестности точки 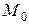 , выполнятся условие
, выполнятся условие 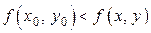 .
.
Как и в случае функции одной переменной такие точки называются экстремальными. При этом не следует смешивать точку экстремума с точкой наибольшего или наименьшего значения функции в некоторой области. Аналогичные определения используются и для функций любого числа переменных.
Теорема 5.13.1 (необходимое условие существования экстремума). Если функция 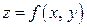 достигает экстремума в точке
достигает экстремума в точке 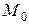 , то каждая частная производная по
, то каждая частная производная по 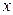 и по
и по 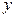 в этой точке равна нулю или не существует.
в этой точке равна нулю или не существует.
Доказательство. Рассмотрим поверхность, которая изображает функцию 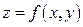 . Если точка
. Если точка 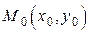 является экстремальной для функции
является экстремальной для функции 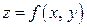 , то в этой точке будет иметь экстремум любая кривая, полученная в результате сечения поверхности произвольной плоскостью, проходящей через
, то в этой точке будет иметь экстремум любая кривая, полученная в результате сечения поверхности произвольной плоскостью, проходящей через 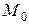 .
.
Рассмотрим вначале сечение плоскостью 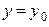 . В этом случае функция приобретает вид:
. В этом случае функция приобретает вид: 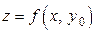 . Но это функция одной переменной, и если она имеет в точке
. Но это функция одной переменной, и если она имеет в точке 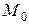 экстремум, то
экстремум, то 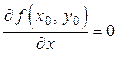 или не существует (п. 2.19). Аналогичный результат получается и для
или не существует (п. 2.19). Аналогичный результат получается и для 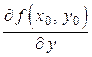 , что и требовалось доказать.
, что и требовалось доказать.
Однако эти условия не являются достаточными для нахождения экстремума. Существуют функции, у которых 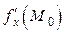 и
и 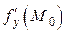 равны нулю или не существуют, но экстремум в точке
равны нулю или не существуют, но экстремум в точке 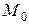 отсутствует. Примером такой функции может служить
отсутствует. Примером такой функции может служить 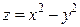 .
.
Точки, в которых производные 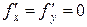 или не существуют, называются критическими или стационарными.
или не существуют, называются критическими или стационарными.
Из вышесказанного следует, что приведенный признак не является достаточным.
Теорема 5.13.2 (достаточное условие существования экстремума). Пусть функция 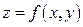 имеет в окрестности точки
имеет в окрестности точки 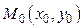 непрерывные частные производные до третьего порядка включительно, а сама точка
непрерывные частные производные до третьего порядка включительно, а сама точка 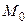 является критической. Тогда при
является критической. Тогда при 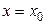 ,
, 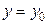 :
:
1) 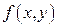 имеет максимум, если
имеет максимум, если 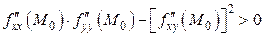 , а
, а 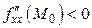 ;
;
2) 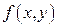 имеет минимум, если
имеет минимум, если 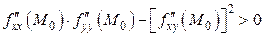 , а
, а 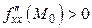 ;
;
3) 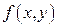 не имеет ни максимума, ни минимума, если
не имеет ни максимума, ни минимума, если 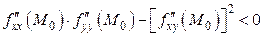 ;
;
4) если 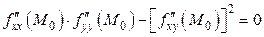 , то необходимы дополнительные исследования.
, то необходимы дополнительные исследования.
Доказательство. Полагая, что 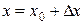 ,
, 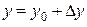 , запишем формулу Тейлора второго порядка для функции
, запишем формулу Тейлора второго порядка для функции 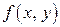 , учитывая, что по условию теоремы
, учитывая, что по условию теоремы 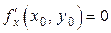 и
и 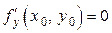 :
:
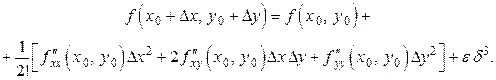
Следовательно,
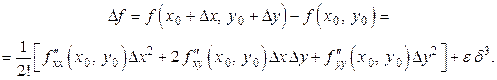
Обозначим 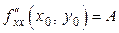 ,
, 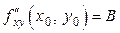 ,
, 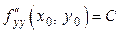 . Кроме того, считая, что угол между направлением отрезка
. Кроме того, считая, что угол между направлением отрезка 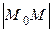 , где
, где 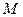 имеет координаты
имеет координаты 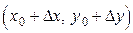 , и осью
, и осью 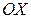 равен
равен 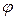 , имеем
, имеем 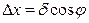 ,
, 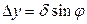 . Подставляя данные выражения в формулу для
. Подставляя данные выражения в формулу для 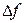 , получаем
, получаем
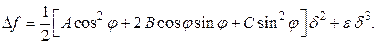
Разделив и умножив выражение, стоящее в квадратных скобках, на 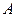 , находим:
, находим:
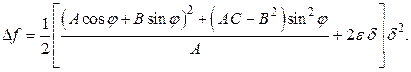 (5.13.1)
(5.13.1)
Рассмотрим теперь, указанные в теореме четыре случая.
1) Пусть 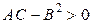 ,
, 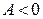 . Тогда в числителе дроби (5.13.1) стоит положительная величина, а сама дробь будет величиной отрицательной, не обращающейся в нуль. Обозначим величину дроби через
. Тогда в числителе дроби (5.13.1) стоит положительная величина, а сама дробь будет величиной отрицательной, не обращающейся в нуль. Обозначим величину дроби через 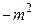 , которая не зависит от
, которая не зависит от 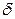 . Тогда
. Тогда
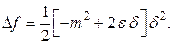
При достаточно малых 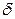 получаем
получаем 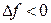 , но согласно определению 5.13.1 это значит, что в точке
, но согласно определению 5.13.1 это значит, что в точке 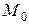 функция достигает максимума.
функция достигает максимума.
2) Пусть 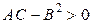 ,
, 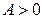 . Проводя аналогичные рассуждения, получаем
. Проводя аналогичные рассуждения, получаем
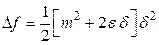 ,
,
что соответствует минимуму функции в точке 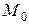 .
.
3) Пусть 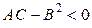 ,
, 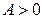 или
или 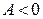 . В этом случае числитель дроби может быть как положительным, так и отрицательным. Все зависит от того, под каким направлением, то есть углом
. В этом случае числитель дроби может быть как положительным, так и отрицательным. Все зависит от того, под каким направлением, то есть углом 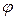 , происходит движение из точки
, происходит движение из точки 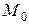 . Следовательно, и величина
. Следовательно, и величина 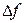 может быть обоих знаков. Если
может быть обоих знаков. Если 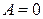 , то
, то 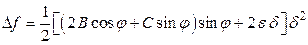 , и знак первого слагаемого, а при малых
, и знак первого слагаемого, а при малых 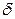 и знак
и знак 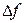 , также будет зависеть от выбора угла
, также будет зависеть от выбора угла 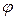 . Это говорит о том, что в одном направлении функция возрастает, а в другом убывает, то есть экстремума в точке
. Это говорит о том, что в одном направлении функция возрастает, а в другом убывает, то есть экстремума в точке 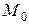 в этих случаях нет.
в этих случаях нет.
4) Пусть 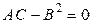 . В этом случае вывод на основании формулы (5.13.1) сделать нельзя. Действительно, при этом
. В этом случае вывод на основании формулы (5.13.1) сделать нельзя. Действительно, при этом
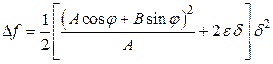 ,
,
и при 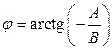 числитель дроби обращается в ноль, то есть знак
числитель дроби обращается в ноль, то есть знак 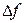 будет определяться знаком
будет определяться знаком 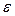 . Следовательно, в данном случае требуется использование или формулы Тейлора более высокого порядка или какого-то другого метода.
. Следовательно, в данном случае требуется использование или формулы Тейлора более высокого порядка или какого-то другого метода.
Условный экстремум
В п. 5.13 показано, как находить экстремум у функции двух переменных с помощью необходимого и достаточного условия. В принципе, аналогичным образом можно провести исследование на экстремум функцию и с большим числом переменных.
Однако бывают случаи, когда у исследуемой функции аргументы связаны между собой дополнительным условием (уравнением связи) и необходимо найти экстремум у заданной функции с учетом данного дополнительного условия. Экстремумы подобного вида называются условными.
Рассмотрим вначале вопрос о нахождении условного экстремума функции двух переменных 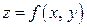 при условии, что ее аргументы
при условии, что ее аргументы 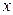 и
и 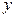 связаны уравнением
связаны уравнением 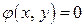 .
.
Например, необходимо найти экстремум функции 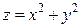 при условии, что
при условии, что 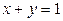 или
или 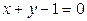 .
.
В принципе данную задачу можно решить следующим образом. Так как переменные 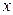 и
и 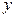 связаны между собой условием
связаны между собой условием 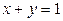 , то найдем из него
, то найдем из него 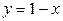 и подставим полученное значение в функцию
и подставим полученное значение в функцию 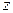 :
:
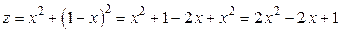 .
.
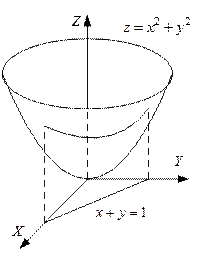 Таким образом, при выполнении наложенного условия функция двух переменных превращается в функцию одной переменной и может быть исследована на экстремум обычными методами. С этой целью находим производную этой функции и приравниваем ее нулю:
Таким образом, при выполнении наложенного условия функция двух переменных превращается в функцию одной переменной и может быть исследована на экстремум обычными методами. С этой целью находим производную этой функции и приравниваем ее нулю: 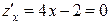 откуда
откуда 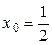 . В данной критической точке при переходе ее слева направо знак производной меняется с минуса на плюс, следовательно, это минимум. Данному значению
. В данной критической точке при переходе ее слева направо знак производной меняется с минуса на плюс, следовательно, это минимум. Данному значению 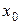 соответствует
соответствует 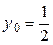 . Итак, в точке
. Итак, в точке 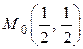 заданная функция достигает минимума по отношению к наложенному условию. Геометрически – это самая низкая точка параболоида, лежащая над прямой
заданная функция достигает минимума по отношению к наложенному условию. Геометрически – это самая низкая точка параболоида, лежащая над прямой 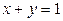 (рис. 5.14.1). Из примера видно, что точка условного экстремума, вообще говоря, не является экстремальной точкой самой функции.
(рис. 5.14.1). Из примера видно, что точка условного экстремума, вообще говоря, не является экстремальной точкой самой функции.
При наличии наложенного условия переменные 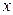 и
и 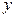 независимыми считать нельзя, так как одна из этих переменных величин может быть выражена через другую. Следовательно, выразив, например,
независимыми считать нельзя, так как одна из этих переменных величин может быть выражена через другую. Следовательно, выразив, например, 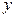 через
через 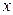 , мы приведем функцию
, мы приведем функцию 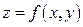 к функции одной переменной, метод исследования которой на экстремум из- Рис. 15.4.1
к функции одной переменной, метод исследования которой на экстремум из- Рис. 15.4.1
вестен.
Однако данная задача достаточно простая и решается сведением функции двух переменных к функции одной переменной. В общем случае, когда и переменных больше двух и дополнительных условий несколько, этого достичь не удается.
Например, из куска жести площадью 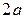 необходимо изготовить закрытую коробку в форме прямого параллелепипеда с наибольшим объемом. Обозначив размеры ее ребер
необходимо изготовить закрытую коробку в форме прямого параллелепипеда с наибольшим объемом. Обозначив размеры ее ребер 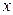 ,
, 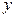 и
и 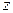 , получаем объем
, получаем объем 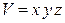 , у которого необходимо определить максимум. Но при этом на переменные
, у которого необходимо определить максимум. Но при этом на переменные 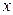 ,
, 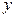 ,
, 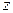 накладывается условие
накладывается условие
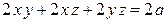 .
.
В данном случае свести задачу к одной переменной не удастся. Следовательно, необходимо найти такой способ решения подобных задач, который основывается на исходном виде функции и заданных ограничений.
Начнем с наиболее простой задачи об экстремуме функции двух переменных 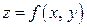 при наложенном ограничении
при наложенном ограничении 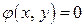 , но в данном случае
, но в данном случае 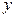 через
через 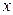 выражать не будем.
выражать не будем.
Очевидно, что при тех значениях 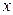 , которые для функции
, которые для функции 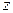 являются экстремальными,
являются экстремальными, 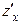 или
или 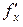 должно быть равно нулю. Найдем
должно быть равно нулю. Найдем 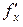 , учитывая, что
, учитывая, что 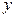 является функцией
является функцией 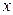 (случай 2, п. 5.6):
(случай 2, п. 5.6):
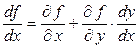 .
.
В точках экстремума
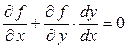 . (15.4.1)
. (15.4.1)
Используя этот же метод, продифференцируем теперь уравнение связи:
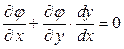 . (15.4.2)
. (15.4.2)
Если умножить теперь равенство (15.4.2) на произвольный коэффициент 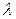 и сложить с равенством (15.4.1), получим:
и сложить с равенством (15.4.1), получим:
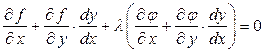
или
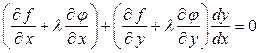 . (15.4.3)
. (15.4.3)
Очевидно, что равенство (15.4.3) должно выполняться во всех точках экстремума. Подберем 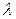 так, чтобы вторая скобка в (15.4.3) обратилась в ноль, но тогда и первая скобка будет равна нулю. В результате получаем два уравнения:
так, чтобы вторая скобка в (15.4.3) обратилась в ноль, но тогда и первая скобка будет равна нулю. В результате получаем два уравнения:
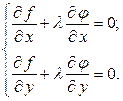 .
.
В этих уравнениях три неизвестных 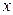 ,
, 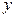 и
и 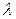 , поэтому необходимо добавить еще одно уравнение, чтобы иметь возможность найти эти неизвестные. Таким уравнением может быть уравнение связи
, поэтому необходимо добавить еще одно уравнение, чтобы иметь возможность найти эти неизвестные. Таким уравнением может быть уравнение связи 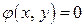 . В результате получаем систему:
. В результате получаем систему:
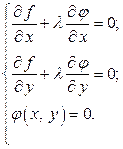 (15.4.4)
(15.4.4)
Решением системы (15.4.4) будут значения неизвестных 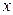 ,
, 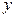 и
и 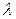 , при которых исходная функция имеет условный экстремум. Следует отметить, что значение
, при которых исходная функция имеет условный экстремум. Следует отметить, что значение 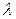 в дальнейшем не понадобится, оно играло лишь вспомогательную роль.
в дальнейшем не понадобится, оно играло лишь вспомогательную роль.
Система (15.4.4) является необходимым условием существования условного экстремума. Прямого указания на вид экстремальной точки она не дает. Обычно ответ на данный вопрос следует из характера задачи.
Можно заметить, что система (15.4.4) получается при дифференцировании функции
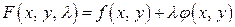
по переменным 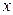 ,
, 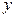 ,
, 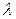 . Эта функция называется функцией Лагранжа, а
. Эта функция называется функцией Лагранжа, а 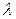 – называется множителем Лагранжа.
– называется множителем Лагранжа.
Итак, для нахождения условного экстремума составляется вспомогательная функция Лагранжа, дифференцируется по всем переменным, эти производные приравниваются нулю, и из полученной системы определяют значения координат экстремальной точки.
Аналогичным образом данная задача решается для любого числа переменных. Пусть необходимо найти экстремумы функции 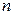 переменных
переменных 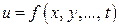 при условии, что переменные
при условии, что переменные 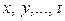 связаны
связаны 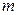
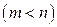 уравнениями
уравнениями
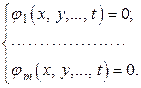
Для определения условного экстремума составляется функция Лагранжа
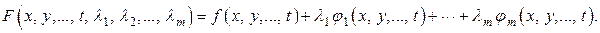
Затем приравниваются нулю все частные производные данной функции, что вместе с ограничениями дает систему из 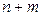 уравнений:
уравнений:
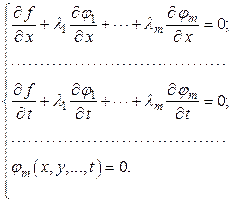
Решение системы дает координаты экстремальной точки. Ее характер определяется в каждой конкретной задаче отдельно.
