Свойства непрерывных функций
Теоремы о непрерывных функциях
Теорема (об устойчивости знака непрерывной функции). Если функция 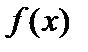 непрерывна в точке
непрерывна в точке 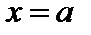 , и если
, и если 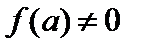 , то найдется такая
, то найдется такая 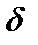 -окрестность точки
-окрестность точки 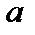 , что для всех значений аргумента из указанной
, что для всех значений аргумента из указанной 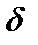 -окрестности функция
-окрестности функция 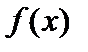 не обращается в нуль и имеет знак, совпадающий со знаком
не обращается в нуль и имеет знак, совпадающий со знаком 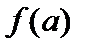 .
.
Определение. Функция 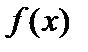 непрерывна на отрезке
непрерывна на отрезке 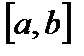 , если она непрерывна в каждой точке внутри отрезка, непрерывна справа в точке
, если она непрерывна в каждой точке внутри отрезка, непрерывна справа в точке 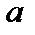
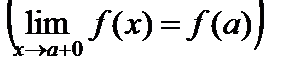 и непрерывна слева в точке
и непрерывна слева в точке 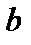
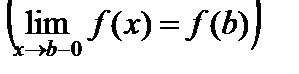 .
.
Теорема (о прохождении непрерывной функции через нуль при смене знака). Пусть функция 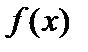 непрерывна на отрезке
непрерывна на отрезке 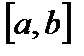 и принимает на концах отрезка значения разных знаков. Тогда внутри отрезка
и принимает на концах отрезка значения разных знаков. Тогда внутри отрезка 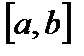 найдется хотя бы одна точка
найдется хотя бы одна точка 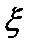 , в которой функция обращается в нуль (
, в которой функция обращается в нуль ( 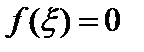 ).
).
Из этой теоремы следует, что если функция 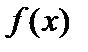 непрерывна на отрезке
непрерывна на отрезке 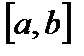 и принимает на концах отрезка значения разных знаков, то уравнение
и принимает на концах отрезка значения разных знаков, то уравнение 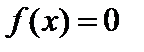 имеет на этом отрезке хотя бы одно решение.
имеет на этом отрезке хотя бы одно решение.
Теорема (о прохождении непрерывной функции через любое промежуточное значение). Пусть функция 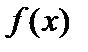 непрерывна на отрезке
непрерывна на отрезке 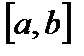 , причем
, причем 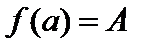 ,
, 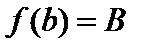 . Пусть
. Пусть 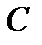 — любое число, заключенное между
— любое число, заключенное между 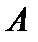 и
и 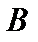 . Тогда на отрезке
. Тогда на отрезке 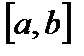 найдется точка
найдется точка 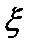 такая, что
такая, что 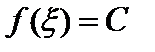 .
.
Прежде, чем сформулировать следующие теоремы напомним определение ограниченной функции.
Определение. Функция 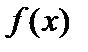 называется ограниченной сверху (снизу) на множестве
называется ограниченной сверху (снизу) на множестве 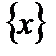 , если найдется такое вещественное число
, если найдется такое вещественное число 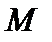 (
( 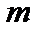 ), что для всех значений аргумента
), что для всех значений аргумента 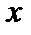 из множества
из множества 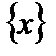 справедливо неравенство
справедливо неравенство 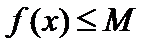 (
( 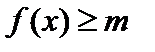 ).
).
Определение. Функция 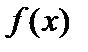 называется ограниченной на множестве
называется ограниченной на множестве 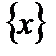 , если она ограничена на этом множестве сверху и снизу, то есть если найдутся такие вещественные числа
, если она ограничена на этом множестве сверху и снизу, то есть если найдутся такие вещественные числа 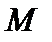 и
и 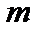 , что для всех значений аргумента
, что для всех значений аргумента 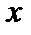 из множества
из множества 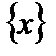 справедливы неравенства
справедливы неравенства 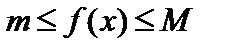 .
.
Заметим, что последнее неравенство можно заменить неравенством 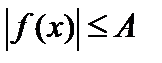 , где
, где 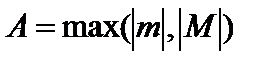 , и сформулировать следующее определение ограниченной функции: функция
, и сформулировать следующее определение ограниченной функции: функция 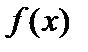 называется ограниченной на множестве
называется ограниченной на множестве 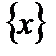 , если найдется такое положительное вещественное число
, если найдется такое положительное вещественное число 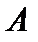 , что для всех значений аргумента
, что для всех значений аргумента 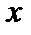 из множества
из множества 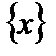 справедливо неравенство
справедливо неравенство 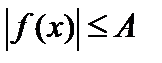 .
.
Функция 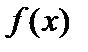 имеет на множестве
имеет на множестве 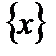 наибольшее значение, если найдется точка
наибольшее значение, если найдется точка 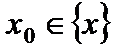 такая что
такая что 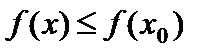 для любого
для любого 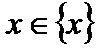 .
.
Функция 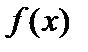 имеет на множестве
имеет на множестве 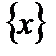 наименьшее значение, если найдется точка
наименьшее значение, если найдется точка 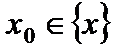 такая что
такая что 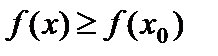 для любого
для любого 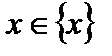 .
.
Теорема (Вейерштрасса) Если функция 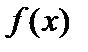 непрерывна на отрезке
непрерывна на отрезке 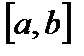 , то она ограничена на этом отрезке и имеет на этом отрезке наибольшее и наименьшее значение.
, то она ограничена на этом отрезке и имеет на этом отрезке наибольшее и наименьшее значение.
Заметим, что если множество 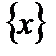 не является отрезком, то функция может быть неограниченной на рассматриваемом множестве и не иметь наибольшего или наименьшего значения.
не является отрезком, то функция может быть неограниченной на рассматриваемом множестве и не иметь наибольшего или наименьшего значения.
Например, функция 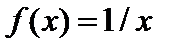 ограничена на отрезке
ограничена на отрезке 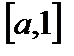 (
( 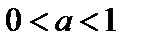 ), имеет наибольшее значение
), имеет наибольшее значение 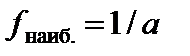 и наименьшее значение
и наименьшее значение 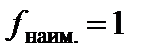 . Однако эта функция будет неограниченной сверху на интервале (0,1) и на этом интервале у нее нет наибольшего значения Заметим также, что несмотря на то, что функция ограничена снизу (
. Однако эта функция будет неограниченной сверху на интервале (0,1) и на этом интервале у нее нет наибольшего значения Заметим также, что несмотря на то, что функция ограничена снизу ( 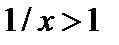 для любого
для любого 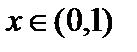 ) она не имеет наименьшего значения, так как 1 не принадлежит области значений функции на рассматриваемом интервале.
) она не имеет наименьшего значения, так как 1 не принадлежит области значений функции на рассматриваемом интервале.
Экспоненциальная функция 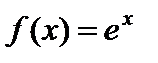 также ограничена на любом отрезке вещественной оси и имеет на этом отрезке наибольшее
также ограничена на любом отрезке вещественной оси и имеет на этом отрезке наибольшее 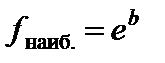 и наименьшее
и наименьшее 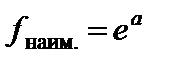 значения, но на всей числовой прямой экспонента неограниченна сверху, следовательно, у нее не существует наибольшего значения. Снизу функция ограничена, так как
значения, но на всей числовой прямой экспонента неограниченна сверху, следовательно, у нее не существует наибольшего значения. Снизу функция ограничена, так как 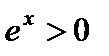 , однако 0 не является наименьшим значением, так не принадлежит области значений функции (нет точки
, однако 0 не является наименьшим значением, так не принадлежит области значений функции (нет точки 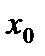 такой, что
такой, что 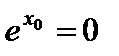 ).
).
