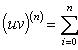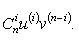Частные производные и дифференциалы фнп
Частной производной от функции 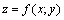 по независимой переменной
по независимой переменной 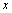 называется производная
называется производная 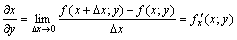 , вычисленная при постоянному.
, вычисленная при постоянному.
Частной производной по y называется производная 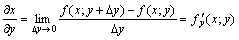 , вычисленная при постоянном х. Для частных производных справедливы обычные правила и формулы дифференцирования.
, вычисленная при постоянном х. Для частных производных справедливы обычные правила и формулы дифференцирования.
Пример 1. 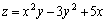 .
.
Рассматривая у как постоянную величину 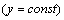 , получим
, получим 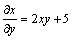 .
.
Рассматривая х как постоянную величину 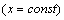 , получим
, получим 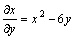 .
.
Дифференциал: Пусть функция u = F(x) определена в области D и 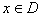 − фиксированная точка. Дадим приращение каждому аргументу хţ :
− фиксированная точка. Дадим приращение каждому аргументу хţ : 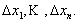 Величину
Величину 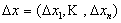 будем называть вектором приращения. В свою очередь функция u получит приращение равное
будем называть вектором приращения. В свою очередь функция u получит приращение равное 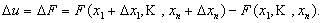
Определение 1. Функция u = F(x) называется дифференцируемой в т. х , если ее приращение может быть представлено в следующем виде: 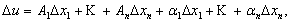
Где - Aţ = Aţ(x) и не зависит от Δх, а 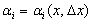 − бесконечно малая при
− бесконечно малая при 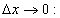
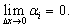
Величина вектора Δх равна: 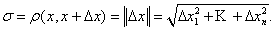
Используя это обозначение, можно написать 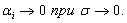
Легко показать, что 
{ 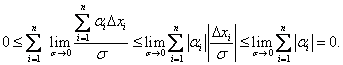 }
}
Определение 2. Главная и линейная часть приращения дифференцируемой функции называется дифференциалом: 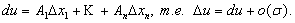
Теорема 1. Функция, дифференцируемая в т. хo − непрерывна в этой точке. { 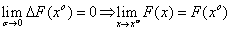 }
}
Теорема 2. (Необходимое условие дифференцируемости) Если F(x) дифференцируема в т. х , то она имеет все частные производные в этой точке, причем 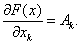
{Пусть 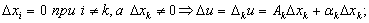 }
}
Отсюда 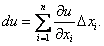 , Если х − независимая переменная, то
, Если х − независимая переменная, то 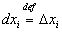 и окончательно
и окончательно 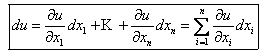
Теорема 3. (Достаточное условие дифференцируемости) Пусть F(x) имеет все частные производные в окрестности т. хо , непрерывные в самой этой точке. Тогда функция дифференцируема в т. хо .
{без доказательства}
Замечание. Для дифференцируемости функции одной переменной достаточно существования производной.
Дифференциал функции u называют полным дифференциалом.
33.Производные и дифференциалы высших порядков ФНП:
Пусть производная некоторой функции f дифференцируема. Тогда производная от производной этой функции называется второй производной функции f и обозначается f". Таким образом,
f"(x) = (f'(x))'.
Если дифференцируема (n - 1)-я производная функции f, то ее n-й производной называется производная от (n - 1)-й производной функции f и обозначается f(n). Итак,
f(n)(x) = (f(n-1)(x))', n ϵ N, f(0)(x) = f(x).
Число n называется порядком производной.
Дифференциалом n-го порядка функции f называется дифференциал от дифференциала (n - 1)-го порядка этой же функции. Таким образом,
dnf(x) = d(dn-1f(x)), d0f(x) = f(x), n ϵ N.
Если x - независимая переменная, то
dx = const и d2x = d3x = ... = dnx = 0.
В этом случае справедлива формула
dnf(x) = f(n)(x)(dx)n.
Производные n-го порядка от основных элементарных функций
Справедливыформулы
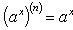
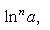
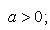
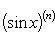
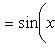
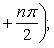
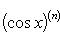
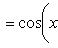
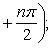
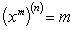
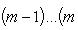
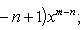
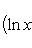
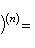
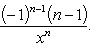
Формула Лейбница:Если u и v - n-кратно дифференцируемые функции, то