Частные случаи приведения пространственной системы сил
Если при приведении системы сил к динамическому винту главный момент динамы оказался равен нулю, а главный вектор отличен от нуля, то это означает, что система сил приведена к равнодействующей, причем центральная ось является линией действия этой равнодействующей.
Выясним, при каких условиях, относящихся к главному вектору 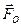 и главному моменту
и главному моменту 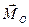 , это может быть. Поскольку главный момент динамы
, это может быть. Поскольку главный момент динамы 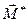 равен составляющей главного момента
равен составляющей главного момента 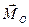 , направленной по главному вектору, то рассматриваемый случай
, направленной по главному вектору, то рассматриваемый случай 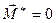 означает, что главный момент
означает, что главный момент 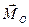 перпендикулярен главному вектору, т.е.
перпендикулярен главному вектору, т.е. 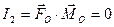 . Отсюда непосредственно вытекает, что если главный вектор
. Отсюда непосредственно вытекает, что если главный вектор 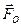 не равен нулю, а второй инвариант равен нулю,
не равен нулю, а второй инвариант равен нулю,
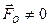 ,
, 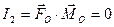 , (7.9) то рассматриваемая система приводится к равнодействующей.
, (7.9) то рассматриваемая система приводится к равнодействующей.
В частности, если для какого-либо центра приведения 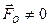 , а
, а 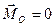 , то это означает, что система сил приведена к равнодействующей, проходящей через данный центр приведения; при этом условие (7.9) также будет выполнено.
, то это означает, что система сил приведена к равнодействующей, проходящей через данный центр приведения; при этом условие (7.9) также будет выполнено.
Обобщим приведенную ранее теорему о моменте равнодействующей (теорему Вариньона) на случай пространственной системы сил.
Если пространственная система сил приводится к равнодействующей, то момент равнодействующей относительно произвольной точки равен геометрической сумме моментов всех сил относительно той же точки.
Пусть система сил имеет равнодействующую 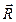 и точка О лежит на линии действия этой равнодействующей. Если приводить заданную систему сил к этой точке, то получим, что главный момент равен нулю.
и точка О лежит на линии действия этой равнодействующей. Если приводить заданную систему сил к этой точке, то получим, что главный момент равен нулю.
Возьмем какой-либо другой центр приведения 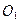 ; тогда
; тогда
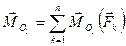 . (7.10) С другой стороны, на основании формулы (4.14) имеем
. (7.10) С другой стороны, на основании формулы (4.14) имеем
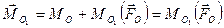 , (7.11) так как
, (7.11) так как 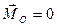 . Сравнивая выражения (7.10) и (7.11) и учитывая, что в данном случае
. Сравнивая выражения (7.10) и (7.11) и учитывая, что в данном случае 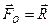 , получаем
, получаем
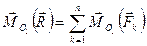 . (7.12) Таким образом, теорема доказана.
. (7.12) Таким образом, теорема доказана.
Пусть при каком-либо выборе центра приведения 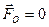 ,
, 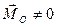 . Так как главный вектор не зависит от центра приведения, то он равен нулю и при любом другом выборе центра приведения. Поэтому главный момент не меняется при перемене центра приведения, и, следовательно, в этом случае система сил приводится к паре сил с моментом
. Так как главный вектор не зависит от центра приведения, то он равен нулю и при любом другом выборе центра приведения. Поэтому главный момент не меняется при перемене центра приведения, и, следовательно, в этом случае система сил приводится к паре сил с моментом 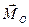 .
.
Составим теперь таблицу всех возможных случаев приведения пространственной системы сил:
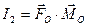 | 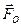 | 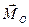 | Случай приведения | |
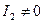 | 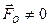 | 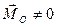 | Динамический винт | |
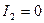 | 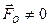 | 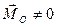 | Равнодействующая | |
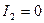 | 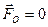 | 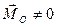 | Пара сил | |
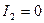 | 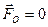 | 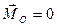 | Система сил эквивалентна нулю |
Если все силы находятся в одной плоскости, например, в плоскости 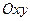 , то их проекции на ось
, то их проекции на ось 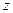 и моменты относительно осей
и моменты относительно осей 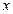 и
и 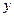 будут равны нулю. Следовательно,
будут равны нулю. Следовательно,
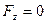 ,
, 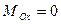 ,
, 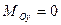 .
.
Внося эти значения в формулу (7.5), найдем, что второй инвариант плоской системы сил равен нулю.
Тот же результат мы получим и для пространственной системы параллельных сил. Действительно, пусть все силы параллельны оси 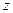 . Тогда проекции их на оси
. Тогда проекции их на оси 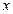 ,
, 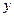 и моменты относительно оси
и моменты относительно оси 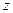 будут равны нулю. Отсюда
будут равны нулю. Отсюда
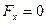 ,
, 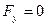 ,
, 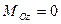 .
.
Пользуясь снова формулой (7.5), найдем 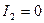 .
.
На основании доказанного можно утверждать, что плоская система сил и система параллельных сил в пространстве не приводятся к динамическому винту.
Задача 7.1.Систему двух сил 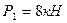 и
и 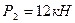 , направленных параллельно осям
, направленных параллельно осям 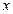 и
и 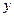 , как указано на рис. (расстояние между точками приложения сил равно
, как указано на рис. (расстояние между точками приложения сил равно 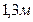 ), требуется привести к динаме, определив главный вектор и главный момент динамы. Найти углы
), требуется привести к динаме, определив главный вектор и главный момент динамы. Найти углы 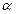 ,
, 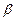 и
и 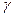 , составляемые нейтральной осью системы с координатными осями, а также уравнение нейтральной оси.
, составляемые нейтральной осью системы с координатными осями, а также уравнение нейтральной оси.
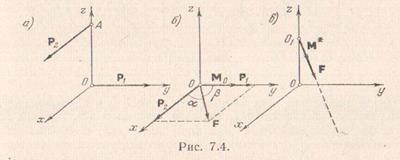
Решение. Возьмем за центр приведения начало координат О. Проекции главного вектора  на оси координат будут
на оси координат будут
 ,
, 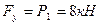 ,
, 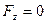 .
.
Модуль главного вектора
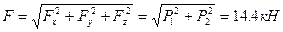 .
.
Направляющие косинусы главного момента равны
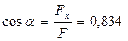 ,
, 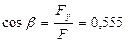 ,
, 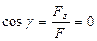 .
.
Найдем проекции главного момента на оси координат:
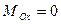 ,
, 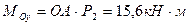 ,
, 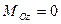 .
.
На рис. показано расположение главного вектора 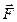 и главного момента
и главного момента 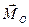 для центра приведения О.
для центра приведения О.
Проекцию главного момента на направление главного вектора определим по формуле
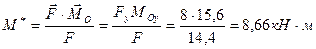 .
.
Уравнение центральной оси (7.8) имеет вид
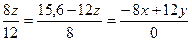 .
.
Отсюда следует, что центральная ось является линией пересечения плоскостей
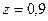 ,
, 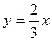 .
.
На рис.7.4 показано расположение этой оси  .
.
Задача 7.2.По ребрам куба со стороной 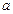 действуют двенадцать равных по модулю сил, как показано на рис. Привести систему к простейшему виду.
действуют двенадцать равных по модулю сил, как показано на рис. Привести систему к простейшему виду.
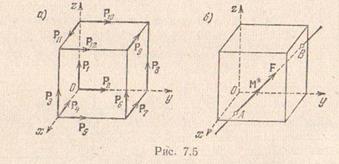
Решение.За центр приведения возьмем начало координат О и вычислим проекции главного вектора 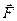 и главного момента на координатные оси. Имеем
и главного момента на координатные оси. Имеем
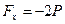 ,
, 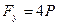 ,
, 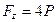 ,
,
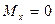 ,
, 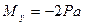 ,
, 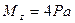 ,
,
где 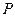 – общее значение модуля заданных сил.
– общее значение модуля заданных сил.
По формулам (7.4) и (7.5) найдем значения статических инвариантов
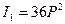 ,
, 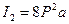 .
.
Так как второй инвариант положителен, то система сил приводится к правому динамическому винту (главный вектор 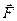 и момент
и момент 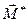 направлены в одну сторону). Модуль момента
направлены в одну сторону). Модуль момента 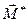 найдем по формуле (7.6):
найдем по формуле (7.6):
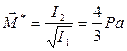 .
.
Напишем уравнение центральной оси (7.8):
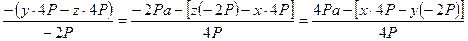 .
.
Отсюда видно, что центральная ось системы представляет линию пересечения плоскостей
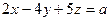 ,
,
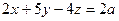 .
.
Подставляя в эти уравнения сначала 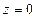 , а затем
, а затем 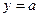 , найдем точки пересечения центральной оси с нижней и боковой гранями куба
, найдем точки пересечения центральной оси с нижней и боковой гранями куба
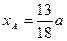 ,
, 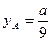 ,
, 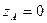 ,
,
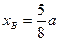 ,
, 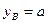 ,
, 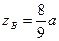 .
.
Таким образом, динамический винт, эквивалентный данной системе сил, состоит из силы 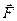 , модуль которой равен
, модуль которой равен 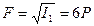 , и пары сил с моментом
, и пары сил с моментом 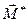 , коллинеарным силе
, коллинеарным силе 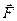 и численно равным
и численно равным 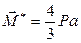 . Центральная ось и составляющие динамического винта показаны на рис.
. Центральная ось и составляющие динамического винта показаны на рис.
